Лабораторная работа №2. Быстрое преобразование Фурье

Цель работы: Изучение Быстрого преобразования Фурье.

Необходимые теоретические сведения

Для выполнения непосредственных вычислений ПФ по формулам (1) и (2), описанного в работе №1 требуется большое количество операций умножения (если точнее, N ² умножений и N ² сложений при условии, что значения exp(– j2πkn/N) вычислены заранее и помещены в таблицу).

		(1)
		(2)

Это существенно снижает скорость преобразования, что во многих случаях является недопустимо (например, в приложениях реального времени). Поэтому были разработаны алгоритмы быстрого преобразования Фурье, сокращающие количество операций (функция MathCAD FFT, которая использовалась в предыдущей работе, использует БПФ). Это сокращение происходит за счет уменьшения повторных операций, используемых для вычисления каждого X [ k ].

Рассмотрим алгоритм БПФ с основанием 2, который применяется к последовательностям длины N =2 ^m, m – целое.

Основную идею БПФ можно пояснить следующими шагами.

1. Последовательность x [ n ] разобьем на две N /2 – точечные последовательности x ₁[ n ] и х ₂[ n ].

2. Найдем для них коэффициенты Фурье X ₁[ k ] и X ₂[ k ] (по ф. (1) для ДПФ).

3. Затем по значениям X ₁[ k ] и X ₂[ k ] можно определить требуемое N –точечное ДПФ X [ k ]. Эта последняя операция выполняется просто и не потребует сложных вычислений (как будет показано ниже – ф. 4). В итоге для вычисления N – точечного ДПФ через два N /2 – точечных ДПФ потребуется выполнить (N /2)²+(N /2)²= N ²/2 операций, т.е. в 2 раза меньше, чем при непосредственном вычислении N –точечного ДПФ.

4. А теперь возьмём и вместо шага 2 (выполнения N /2 – точечных ДПФ) разобьём N /2 – точечные последовательности x ₁[ n ] и х ₂[ n ] на две N /4 – точечные последовательности каждую x ₁₁[ n ], х ₁₂[ n ] и x ₂₁[ n ], х ₂₂[ n ].

5. Найдем для них свои ДПФ X ₁₁[ k ], X ₁₂[ k ] и X ₂₁[ k ], X ₂₂[ k ].

6. По типу упомянутой на шаге 3 объединительной операции соединим первые две N /4 – точечные последовательности между собой с образованием N /2 – точечной последовательности X ₁[ k ]. Вторые две N /4 – точечные последовательности аналогично объединим между собой с образованием второй N /2 – точечной последовательности X ₂[ k ].

7. Вернёмся к шагу 3 и выполним объединение N /2 – точечных последовательностей X ₁[ k ] и X ₂[ k ]. В этом случае потребуется выполнить [(N /4)²+(N /4)²]+[(N /4)²+(N /4)²]= N ²/4 умножений, т.е. в 4 раза меньше, чем при непосредственном вычислении N –точечного ДПФ.

8. Не остановимся на этом и продолжим процесс разбиения на группы на шаге 5 и т.д. и объединение результатов промежуточных ДПФ, аналогично шагам 6 и 3. В пределе, при последовательном разбиении будут получены начальные группы по 2 точки. Т.е. описанная процедура является рекурсивной (рис. 1). Таким методом можно существенно сократить количество операций.

Рисунок 1 – Дерево рекурсии для 8 элементов

Рассмотрим математическое обоснование метода. Для упрощения рассуждений пока не будем учитывать деление суммы на N (ф. 1).

Представим последовательность x [ n ] как сумму двух последовательностей x ₁[ n ] и х ₂[ n ] длиной N /2 каждая (четных и нечетных отсчетов соответственно, см. формулу (3)).

Последовательность х ₂[ n ] сдвинута (запаздывает) относительно последовательности x ₁[ n ] на половину шага, т.е. на 1/2 (рис. 2).

Рисунок 2 – Разложение x [ n ] на две последовательности x 1[ n ] и х 2[ n ] (в скобках указаны номера исходной последовательности)

Тогда в силу свойства суперпозиции ДПФ преобразование от суммы последовательностей будет равно сумме преобразований:

X [ k ]=F{ x [ n ]}=F{ x ₁[ n ]+ х ₂[ n -1/2]}=F{ x ₁[ n ]}+F{ х ₂[ n -1/2]}= .

Т.к. , , , то

.

Здесь выражения в фигурных скобках представляют прямые N /2 – точечные ДПФ от последовательностей x ₁[ n ] и х ₂[ n ].

Введем обозначение .

Тогда

(4)

Это и есть объединительная операция, указанная в пп. 3, 6 и т.д. Из формулы (4) следует, что N – точечное ДПФ X [ k ] может быть вычислено через два N /2 – точечных ДПФ X ₁[ k ] и X ₂[ k ].

Согласно изложенным рассуждениям, была найдена лишь половина значений X [ k ], т.к. 0≤ k ≤ N /2-1. Следует иметь в виду, что отсчеты ДПФ для последовательностей х ₁[ n ] и х ₂[ n ] повторяются с периодом N /2 (в силу свойства периодичности коэффициентов ДПФ, т.е. периодичности спектра). Поэтому

(5)

Из (4) и (5) получаем выражение для определения второй части спектральных коэффициентов X [ k ]:

,

а учитывая равенство ,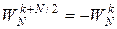

(6)

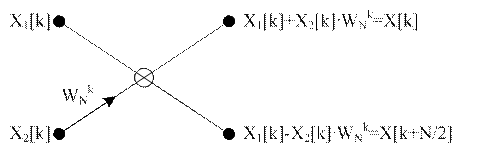
Формулы (4) и (6) представляют базовую операцию БПФ (так называемую «бабочку» – операцию объединения). Схематическое изображение "бабочки" показано на рис. 3. Здесь X ₁[ k ] и X ₂[ k ] обозначают точки с одинаковыми номерами из разных подгрупп (фактически k – это номер бабочки), а кружок в центре обозначает операцию сложения/вычитания. Стрелка обозначает операцию умножения на . Жирные точки обозначают ячейки памяти, содержащие входные и выходные значения для отдельных этапов БПФ.

Рисунок 3 – Основная операция БПФ

На рис. 4 показана схема вычисления 8 – точечного БПФ с использованием двух 4 – точечных преобразований (шаги 1 - 3).

Рисунок 4 – Вычисление 8–точечного БПФ

В свою очередь, 4 – точечные преобразования могут быть определены через 2 – точечные (шаги 4 - 6), которые вычисляются по формулам:

(7)

(8)

На рис. 5 показан результирующий граф 8 – точечного БПФ.

Рисунок 5 – Результирующий граф 8–точечного БПФ

Описанный алгоритм БПФ называется алгоритмом с прореживанием по времени, так как здесь требуется перестановка входных значений x [ n ] (см. рис. 4). Алгоритм, при реализации которого входные отсчеты не переставляются, а требуется перестановка отсчётов X [ k ], называются алгоритмами с прореживанием по частоте.

Поскольку произведение 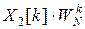можно после вычисления запомнить, то для каждой базовой операции БПФ необходимо выполнять только умножение X ₂[ k ] на множитель W_N^k. Входные и выходные значения базовых операций обычно хранят в одних и тех же ячейках памяти. На одну базовую операцию приходится одна дополнительная ячейка для хранения произведения . Поэтому входная x [ n ] и выходная X [ k ] последовательности, а также промежуточные результаты могут размещаться в одном и том же массиве ячеек памяти. Алгоритм БПФ, использующий указанные возможности, называют алгоритмом с замещением.

Особенностью рассматриваемых алгоритмов БПФ является необходимость перестановки входных или выходных значений. Элементы входной последовательности для алгоритма с прореживанием по времени должны быть расположены в памяти в бит–инверсном порядке. Бит–инверсный порядок задается путем «зеркального» отображения двоичных разрядов входной последовательности (табл. 1).

Таблица 1 – Бит–инверсный порядок

Процедуру перестановки входных значений (прореживание по времени) – битинверсию в MathCad можно реализовать перестановкой, как показано на рис. 6.

Рис. 6. Процедура бит – инверсии в MathCad

На всех этапах выполнения БПФ используются коэффициенты W_N^k, k =0,1,... N –1. Обычно при практической реализации указанные коэффициенты вычисляют до выполнения БПФ и хранят в таблице, к которой можно обращаться в процессе счета.

Количество этапов БПФ равно , количество "бабочек" на каждом этапе – N /2. Так как в процессе БПФ используются комплексные числа, то каждая «бабочка» БПФ сопровождается четырьмя операциями умножения и сложения. Поэтому количество парных операций умножение–сложение равно . При больших N применение алгоритма БПФ существенно сокращает количество операций, требуемых для вычисления ДПФ.

Если БПФ выполняется на микроконтроллере (микропроцессоре), в котором не реализованы операции с комплексными числами, то кроме массива X для действительных частей, необходимо использовать массив Y для мнимых. Если исходный сигнал представлен действительной последовательностью, то функция Swap() применяется только для массива x, а массив для мнимых частей просто обнуляется. Алгоритм БПФ рассчитан на комплексный входной сигнал и при наличии мнимых частей функцию Swap() необходимо было бы применить и для массива y.

Указания к выполнению работы

Данная работа выполняется на ПЭВМ с использованием программы MathCAD 2001.

Для лучшего понимания принципа программной реализации БПФ следует иметь в виду:

1. БПФ выполняется в несколько этапов (римские цифры на рис 5). На первом этапе используется двухточечное ДПФ, т.е. количество точек в каждом домене (обведены пунктиром) M =2. Всего имеется N точек, значит количество доменов D на этапе равно N/M (N/2). Т.к. одну бабочку образуют 2 точки, а в домене M точек, то количество бабочек в одном домене K= M /2 (K= M /2 = 1). Номера бабочек в домене k изменяются от 0 до K -1 (K -1= M/2-1= 0). Значит, на первом этапе все W_M^k одинаковы и равны W ₂⁰.

2. На втором этапе используется четырехточечное БПФ, т.е. в каждом домене количество точек M=4. Количество доменов D равно N/M (N/4). Количество бабочек в каждом домене K= 2 ( K= M/2= 2), k в домене изменяется от 0 до 1 (до K -1= 1). Значит, на втором этапе W_M^k будут равны W ₄⁰ и W ₄¹. При переходе в другой домен переменная k обнуляется (начинается новый цикл перебора бабочек домена) и коэффициенты снова будут W ₄⁰ и W ₄¹.

3. На III этапе M=8, D = N/8, K= M /2=4, k от 0 до 3, W_M^k = { W ₈⁰, W ₈¹, W ₈², W ₈³}. И т.д. по такому же принципу.

4. Половину точек любого домена составляют верхние точки бабочек, половину – нижние. Поэтому расстояние между точками одной бабочки равно M/2, т.е. если верхняя точка внутри домена имеет индекс k, то пару ей в бабочке составит точка с индексом k + M/2.

Date: 2016-05-23; view: 2227; Нарушение авторских прав