
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа №6. Синтез рекурсивных цифровых фильтров
|
|
Цель работы: Изучить синтез рекурсивных фильтров методом аналогового прототипа.
Теоретическая часть
Процесс проектирования рекурсивного частотного фильтра обычно заключается в задании необходимой передаточной характеристики фильтра в частотной области и ее аппроксимации с определенной точностью какой-либо непрерывной передаточной функцией, с последующим z-преобразованием для перехода в z-область. Первые две операции хорошо отработаны в теории аналоговой фильтрации сигналов, что позволяет использовать для проектирования цифровых фильтров большой справочный материал по аналоговым фильтрам. Последняя операция является специфичной для цифровых фильтров.
Для алгебраического преобразования непрерывной передаточной функции в многочлен по z используется билинейное преобразование, известное в теории комплексных переменных под названием дробно-линейного преобразования. [3]
1 Передаточные функции и формы реализации
1.1 Рекурсивные фильтры
Рекурсивные фильтры (РФ) своим названием обязаны наличием «обратной связи» – выходной сигнал снова подается на вход системы (рис.1).
Как правило (заметим, что не всегда), рекурсивные цифровые фильтры, в отличие от нерекурсивных, обладают бесконечной импульсной характеристикой, поэтому их часто называют БИХ-фильтрами. Их работа подчиняется разностному уравнению общего вида:
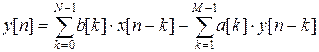 , ,
| (1) |
а передаточная функция равна
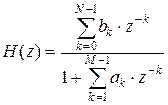 . .
| (2) |
Как было сказано, нельзя автоматически отождествлять НРФ и БИХ фильтры. Например, отсчеты импульсной характеристики рекурсивной цепи с передаточной функцией
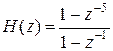
будут конечными и равными 1 только для n = 0, 1, 2, 3, 4, а для n ≥ 5 h [ n ]=0 (прямое деление числителя на знаменатель дает: H (z) = 1+ z -1+ z -2+ z -3+ z -4). Значит, этот рекурсивный фильтр имеет конечную импульсную характеристику. Поэтому в дальнейшем будем говорить про проектирование НРФ.
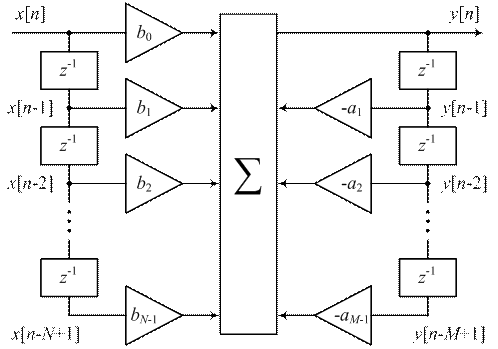
|
| Рисунок 1 – Структурная схема рекурсивного цифрового фильтра (прямая форма реализации) |
Нули передаточной функции являются корнями числителя (2), т. е. значениями переменной z, обращающими в нуль полином B(z).
Полюсы соответствуют корням знаменателя передаточной функции (2).
В частном случае, когда все коэффициенты левой части, кроме нулевого, равны 0 (рис. 3), передаточная функция:
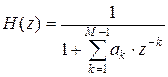 . .
| (3) |
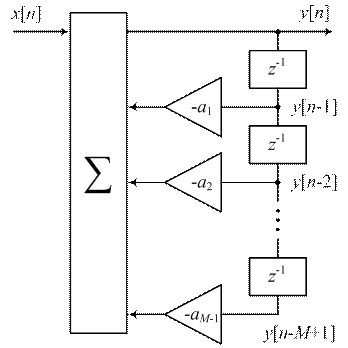
|
| Рисунок 3 – Структурная схема рекурсивного цифрового фильтра без нулей передаточной функции |
При синтезе дискретных частотных рекурсивных фильтров нужно найти такие коэффициенты передаточной функции (2) или (3), частотная характеристика которой удовлетворяла бы нормам ослабления фильтра в полосах пропускания и непропускания (рис. 3 из предыдущей работы).
Одно из важнейших свойств рекурсивных фильтров - возможность получения узких переходных зон при конструировании частотных фильтров, так как функция H(z) фильтра может резко изменяться при приближении к нулю многочлена в знаменателе (2), (3).
Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчетов для текущих вычислений может приводить к накапливанию ошибок.
Рекурсивные фильтры являются фазосдвигающими фильтрами. Если требуется обеспечить нулевой фазовый сдвиг, то операция фильтрации производится дважды, в прямом и обратном направлении числовой последовательности массива данных, при этом амплитудно-частотная характеристика (АЧХ) фильтрации будет равна |H(ω)|2 фильтра, что необходимо учитывать при конструировании фильтра.
1.2 Формы реализации рекурсивных фильтров
РФ порядка выше второго (по числу полюсов или порядку М общего разностного уравнения (1) реализуются, как правило, путем последовательного или параллельного соединения базовых звеньев второго порядка, что соответствует каскадной (последовательной) и параллельной формам их реализации. Базовые биквадратные звенья РФ выполняются в соответствии с прямой или канонической формами реализации РФ. Число последовательных или параллельных звеньев L при четном порядке фильтра M находится как L = М /2, а при нечетном – как L = (M +1)/2, при этом одно звено фильтра является звеном первого порядка (звеном с одним вещественным полюсом).
Передаточная функция каскадно реализуемого РФ (рис. 3) определяется произведением передаточных функций его звеньев:
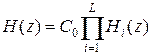 ,
где ,
где 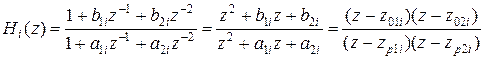 . .
| (4) |
где Hi (z) – передаточная функция i -го биквадратного звена при значении коэффициента b 0 i = 1; С 0 – нормирующий или масштабирующий множитель.

|
| Рисунок 3 – Каскадная структура ЦФ |
Если одно из звеньев является звеном первого порядка, то для него коэффициенты b 2 i и a 2 i в (4) равны нулю.
Входным сигналом i -го звена xJ (n) в такой структуре является выходной сигнал yi –1[ n ] предыдущего (i − 1)-го звена: xi [ n ] = yi –1[ n ].
Коэффициенты звеньев и их полюсы, нули связаны соотношениями:
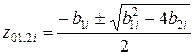 ; ; 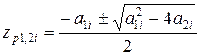 ; ;
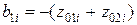 ; ; 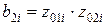 ; ;
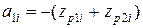 ; ; 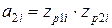 . .
| (5) |
Пары нулей и полюсов, определяющие значения коэффициентов i -го звена, могут быть вещественными разными, вещественными равными, а при 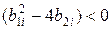 и
и 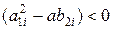 − комплексно-сопряженными:
− комплексно-сопряженными:
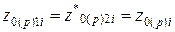 .
.
В этом случае соотношения (5) принимают вид
| b 1 i = –2Re{ z 0 i }= –2 r 0 i cos w 0 i, b 2 i =| z 0 i |2= r 20 i, a 1 i = –2Re{ zpi }= –2 rpi cos wpi, a 2 i =| zpi |2= r 2 pi, | (6) |
где w 0(p) i = ω0(p) i T д − нормированная частота нуля или полюса.
Для звена первого порядка b 1= − z 01, a 1= − zp 1.
Передаточная функция параллельно реализуемого РФ (рис. 4) определяется суммой передаточных функций звеньев Hi (z), а также константы С:
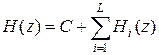 ,
где ,
где 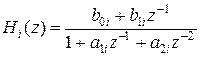 . .
| (7) |
Если одно из звеньев является звеном первого порядка, то для него коэффициенты b 1 i и a 2 i в (7) равны нулю.
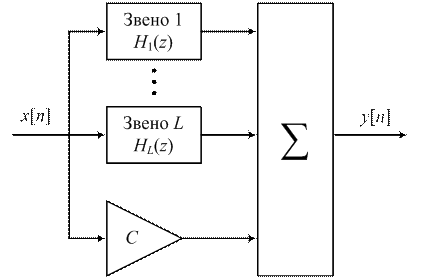
|
| Рисунок 4 – Параллельная структура ЦФ |
Выходной сигнал фильтра равен сумме выходных сигналов звеньев:
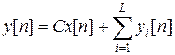 .
.
Передаточная функция, соответствующая параллельной структуре РФ, получается разложением на простые дроби передаточной функции фильтра, представленной в полиномиальной или нуль-полюсной форме. При этом порядок числителя передаточной функции звеньев параллельной структуры Hi (z) (7) на единицу меньше порядка знаменателя передаточной функции.
Коэффициенты a 1 i и a 2 i (7) определяются полюсами фильтра с помощью тех же соотношений, что и для каскадно реализуемого РФ.
Коэффициенты b 0 i и b 1 i связаны с нулями и полюсами фильтра через вычеты его передаточной функции в полиномиальной или нуль-полюсной форме, вычисляемые в полюсах передаточной функции zpi:
| b 0 i = res(zp 1 i + zp 2 i ); b 1 i = − zp 2 i res(zp 1 i ) − zp 1 i res(zp 2 i ). | (8) |
В случае комплексно-сопряженных полюсов 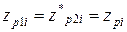 выражения (8) преобразуются к виду
выражения (8) преобразуются к виду
| b 0 i = 2Re{res(zpi)}; b 1 i = − 2Re{ zpi res*(zpi)}. | (9) |
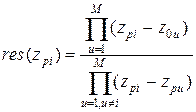 , i = 1,2,…, M. , i = 1,2,…, M.
| (10) |
Коэффициент С в выражении для передаточной функции связан с нулями и полюсами фильтра соотношением 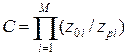 .
.
Коэффициенты С, b 0 i и b 1 i можно выразить также через коэффициенты каскадной формы РФ, которые связаны с полюсами, нулями фильтра более простой зависимостью.
Формы реализации биквадратных звеньев
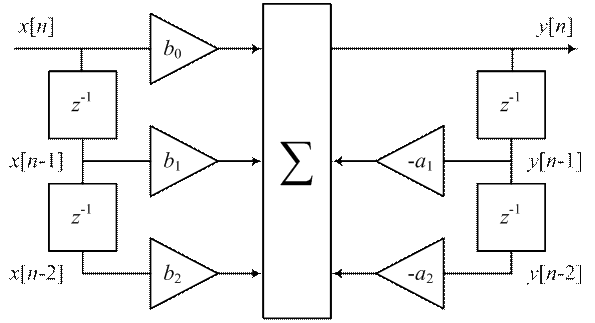
Прямая форма реализации биквадратного звена (рис. 5) описывается разностным уравнением вида
| y [ n ]= b 0 x [ n ]+ b 1 x [ n − 1]+ b 2 x [ n − 2 ] − a 1 y [ n − 1] − a 2 y [ n − 2]. | (11) |
|
| Рисунок 5 – Структура биквадратного звена для прямой формы реализации |
Символом z−1 на схеме обозначен элемент задержки или запоминания сигнала на один период дискретизации Т д.
Уравнению звена (11) эквивалентна также пара разностных уравнений вида
u [ n ]= b 0 x [ n ]+ b 1 x [ n − 1]+ b 2 x [ n − 2 ],
y [ n ]= u [ n ] − a 1 y [ n − 1] − a 2 y [ n − 2],
которые раздельно описывают нерекурсивную и чисто рекурсивную части звена при прямой форме его реализации.
Для аппаратной реализации звена необходимы 4 элемента памяти, сумматор на 5 входов и 5 умножителей (при b 0 = 1 число умножителей 4).
При программной реализации нужно выполнить 5 (или 4) операций умножения и 4 операции сложения на 1 отсчет сигнала.
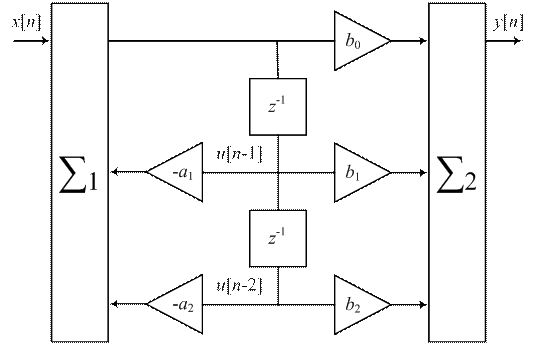
Каноническая форма реализации звена 2-го порядка (рис. 6) имеет в 2 раза меньшее число элементов памяти z −1.
|
| Рисунок 6 – Структурная схема биквадратного звена для канонической формы его реализации |
Такое звено описывается двумя разностными уравнениями:
| u [ n ]= x [ n ] − a 1 u [ n − 1] − a 2 u [ n − 2], y [ n ]= b 0 u [ n ] + b 1 u [ n − 1]+ b 2 u [ n − 2 ]. | (9) |
первое из которых соответствует разностному уравнению рекурсивной, а второе − нерекурсивной части звена в канонической форме. Эти уравнения подобны приведенной выше паре разностных уравнений звена в прямой форме, если поменять местами его нерекурсивную и рекурсивную части и обозначения символов.
Очевидно, что прямая и каноническая формы реализации звеньев могут быть легко обобщены и на РФ, порядок которых выше 2. Однако каскадная и параллельная формы реализации имеют определенные преимущества с точки зрения модульности структуры и меньшей чувствительности к влиянию конечной разрядности чисел. При этом наиболее часто используемой является каскадная форма реализации РФ, что связано с особенностями форматирования коэффициентов фильтров и большей их однородностью, т.е. степенью близости.
Из других структур РФ интерес, с точки зрения реализации, представляет дуальная или обращенная каноническая структура биквадратного звена (рис. 7). При построении дуальных структур входы заменяются выходами, сумматоры узлами, а узлы сумматорами.
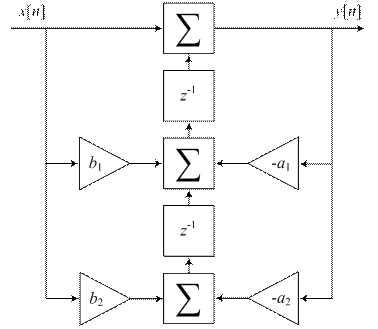
|
| Рисунок 7 – Дуальная каноническая структура биквадратного звена |
2 Методы синтез цифрового РФ по аналоговому прототипу
Решение задачи синтеза рекурсивных фильтров сводится к нахождению коэффициентов b [ k ]и a [ k ] (2, 3). Известны прямые и косвенные методы синтеза рекурсивных фильтров [Бондарев, 131]. Прямые методы основаны на непосредственном определении параметров цифровых РФ по заданным временным или частотным характеристикам. Косвенные (по аналоговому прототипу) методы синтеза РФ основаны на дискретизации аналогового фильтра, удовлетворяющего заданным требованиям.
Существуют также прямые методы расчета цифровых фильтров в частотной или временной областях, которые образуют вторую группу методов расчета цифровых фильтров. К ним относятся как методы расчета по заданному квадрату амплитудной характеристики, так и методы расчета во временной области.
Основным способом проектирования рекурсивных фильтров является проектирование по аналоговому прототипу.
Требуемая частотная характеристика фильтра в виде кусочно-линейной аппроксимации, показанная на рис. 1, нереализуема. Поэтому при синтезе АФП на первом этапе выполняют аппроксимацию желаемой АЧХ, подбирая передаточную функцию фильтра таким образом, чтобы она была реализуемой и удовлетворяла требованиям, заданным при проектировании. На практике широко применяют аппроксимацию АЧХ полиномами и дробями.
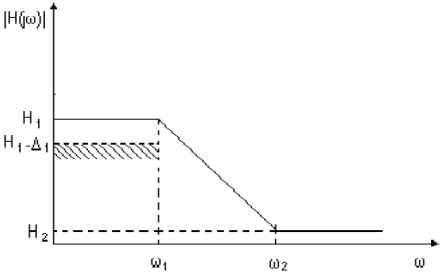
|
| Рисунок 1 – Требования к АЧХ |
К полиномиальным относятся аппроксимации Тейлора (фильтры Баттерворта), Чебышева, к дробным – Кауэра–Золоторева (эллиптические фильтры), Чебышева инверсная. Передаточные функции фильтров с полиномиальной аппроксимацией не имеют конечных нулей, их частотные характеристики монотонны в полосе задерживания.
У фильтров с дробной аппроксимацией передаточные функции имеют нули на конечных частотах в полосе задерживания, а частотные характеристики – пульсации (в том числе равноволновые) в полосе задерживания. Фильтры Чебышева и эллиптические имеют равноволновые пульсации и в полосе пропускания.
С целью унификации общепринято применять нормирование по частоте, приводящее расчет различных типов фильтров (ФВЧ, ФНЧ, ПФ, ЗФ) к нормированному фильтру нижних частот с граничной частотой пропускания (частотой среза) = 1 (заметим, что при нормировании по частоте для нерекурсивных фильтров 1 равна частота дискретизации). В дальнейшем переход от низкочастотного фильтра-прототипа к требуемому фильтру выполняют с помощью специальных преобразований частоты.
Типичные графики частотных характеристик нормализованного аналогового фильтра-прототипа низкой частоты (АФПНЧ) 4-го порядка с полиномиальной и дробной аппроксимациями приведены на рис. 2.
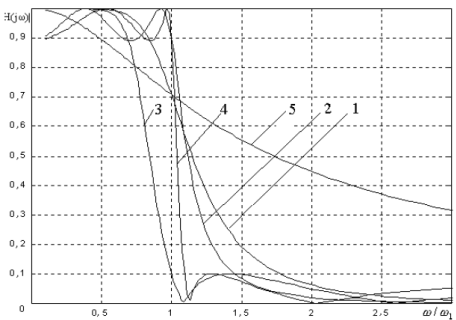
|
| Рисунок 2 – АЧХ ФНЧ 4-го порядка (1 - Баттерворта; 2- Чебышева; 3- инверсный Чебышева; 4- Кауэра; 5- Бесселя) |
Синтез цифрового РФ по аналоговому прототипу возможен методами:
- отображения дифференциалов, заключающемся в дискретизации дифференциального уравнения аналоговой цепи, т.е. переходе от производных к конечным разностям;
- инвариантности импульсных характеристик, основанном на дискретизации импульсной характеристики аналоговой цепи;
- согласованного Z-преобразования;
- билинейного преобразования или инвариантности частотных характеристик
Ни одним из трех первых методов не достигается необходимое соответствие частотных свойств ЦФ и аналогового прототипа. Такое соответствие при синтезе ЦФ со ступенчатообразными АЧХ обеспечивает метод билинейного преобразования или инвариантности частотных характеристик.
В этом методе синтезируемому ЦФ ставится в соответствие некоторый аналоговый фильтр-прототип (АФП) с передаточной функцией Н (р) и частотной характеристикой H (j W), однозначно связанными с передаточной функцией H (z) и частотной характеристикой H (j ω) ЦФ.
Достоинства и недостатки [Рабинер. Теория и применение ЦОС]
Итак, билинейное преобразование обеспечивает простое отображение между аналоговыми и цифровыми фильтрами и является алгебраическим преобразованием, при котором ось jω полностью отображается в единичную окружность на z-плоскости. Кроме того, ему присуще свойство отображать физически реализуемый устойчивый аналоговый фильтр также в физически реализуемый и устойчивый цифровой фильтр. Более того, аналоговые широкополосные фильтры с резкими скатами могут быть отображены в широкополосные цифровые фильтры с резкими скатами без искажений частотной характеристики, связанных с наложениями, которые характерны для метода инвариантного преобразования импульсной характеристики.
Недостаток метода билинейного преобразования заключается в том, что эффекты нелинейности соотношения между частотными шкалами аналогового и цифрового фильтров удается учесть лишь в том случае, когда частотная характеристика аналогового фильтра имеет вид ступенчатообразной функции. Кроме того, при билинейном преобразовании ни импульсная, ни фазовая характеристики аналогового и цифрового фильтров не будут совпадать.
2.2 Последовательность синтеза РФ по аналоговому прототипу с помощью билинейного преобразования
Рассмотрим проектирование конкретных типов фильтров при их каскадной реализации звеньями второго порядка.
Перед тем как перейти к конкретным фильтрам, необходимо сделать два замечания.
Во-первых, в теории фильтров принято иметь дело не с обычной угловой частотой ω, а с нормированной частотой w= ω/ωн, где ωн — нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания ωp, так что wp = ωp / ωн = 1.
Во-вторых, имеет смысл подробно изучать только фильтры нижних частот, так как остальные типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты) или, как принято говорить, с помощью преобразования частоты.
Синтез рекурсивных фильтров непосредственно в z-области возможен только для фильтров простого типа (режекторных и селективных) с ограниченным количеством полюсов и нулей (особых точек). В общем случае, процесс проектирования рекурсивного частотного фильтра обычно заключается в задании необходимой передаточной характеристики фильтра в частотной области и ее аппроксимации с определенной точностью какой-либо непрерывной передаточной функцией, с последующим z-преобразованием для перехода в z-область. Для алгебраического преобразования непрерывной передаточной функции в многочлен по z используется билинейное преобразование, известное в теории комплексных переменных под названием дробно-линейного преобразования.
Рекурсивные ЦФ не обладают строго линейными ФЧХ. В связи с этим в случае неминимально-фазовых фильтров приходится рассматривать аппроксимацию заданных АЧХ и ФЧХ. Если же требования к ФЧХ не предъявляются (минимально-фазовый фильтр), то проектирование избирательного ЦФ удобно осуществлять по заданному квадрату АЧХ.
Нормировка частоты ФНЧ-прототипа
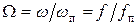
уменьшает на единицу число свободных параметров, что снижает трудоёмкость процедуры синтеза его передаточной функции H (p).
Частотная характеристика аналогового фильтра определена на всей положительной полуоси частот, в то время как у дискретного фильтра она имеет тот же смысл только до частоты 0,5 f д, затем она периодически повторяется (рис. 4).
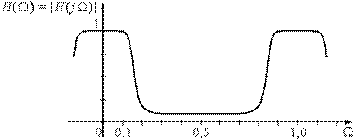
|
| Рисунок 4 – Периодический характер АЧХ дискретного фильтра |
Таким образом, частотная ось сжимается до конечных размеров и шкала частот дискретного фильтра оказывается деформированной относительно шкалы частот аналогового фильтра:
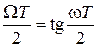 ,
,
где ω - реальная частота, т.е. частота проектируемого ЦФ; Ω - расчетная частота, т.е. частота вспомогательного АФ – прототипа; T – период частоты дискретизации (шаг дискретизации).
Учитывая это при z-преобразовании для цифрового фильтра, до начала расчетов фактические значения задаваемых частотных характеристик (значения ωс, ωp и ωs) следует перевести в значения деформированных частот (аналоговых частот) по выражению:
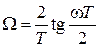 , -π/ T < ω < π/ T. , -π/ T < ω < π/ T.
| (1.1) |
3 Низкочастотный фильтр Баттерворта
3.1 Передаточная функция
Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характеристики в переходной области, т.е. между полосами пропускания и задерживания. Его амплитудно-частотная характеристика задаётся следующей формулой:
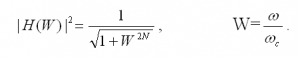
где N – определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность увеличить крутизну спада от полосы пропускания к полосе подавления.
Выбирая фильтр Баттерворта мы ради плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза ωc – эта частота обычно соответствует точке -3 дБ.
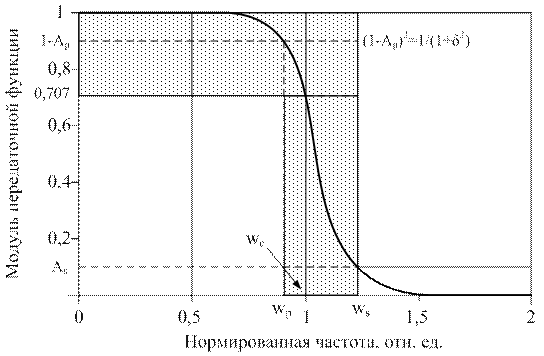
Гладкий вид амплитудно-частотной характеристики аналогового нормированного ФНЧ Баттерворта (рис. 3) задают квадратом передаточной функции вида:
| | H (j W)|2 = H (j W)∙ H (– j W) = 1/(1+W2 N ), | (1.1) |
где W = Ω/Ωс - нормированная частота, Ωс - частота среза АЧХ фильтра, на которой | H (Ω)|2 = 1/2 (соответственно H (Ω) = 0,707, или 3 дб), N - порядок фильтра, определяющий крутизну среза АЧХ. Функция | H (W)|2 – представляет собой энергетический спектр сигнала (спектральную плотность мощности) и не имеет фазовой характеристики, т.е. является четной вещественной, образованной произведением двух комплексно сопряженных функций H (j W) и H *(j W), при этом порядок фильтра N определяет число полюсов функции H(W) и комплексно сопряженных с ними. При W → 0 коэффициент передачи фильтра стремится к 1.
|
| Рисунок 3 – АЧХ фильтра Баттерворта низкой частоты |
1.2 Крутизна среза
Наклон частотной характеристики фильтра при переходе от области пропускания к области подавления можно характеризовать коэффициентом крутизны среза фильтра K в децибелах на октаву:
| K = 20 log| H (ω2)/ H (ω1)|, | (1.2) |
где ω1 и ω2 - частоты с интервалом в одну октаву, т.е. ω2 = 2 ω1.
Длительность импульсной характеристики (реакции) фильтра в пределах ее значимой части также зависит от крутизны среза: чем больше крутизна, тем больше длительность импульсной характеристики (импульсного отклика) фильтра.
1.3 Порядок фильтра
Принимая ω1 = Wc, ω2 = Ws и подставляя в (1.2) значения H (W) с приведенными данными, получим приближенное выражение для определения порядка фильтра по заданному значению K:
| N = K /6. | (1.6') |
Например, для гарантированного ослабления сигнала в полосе подавления в 100 раз (40 децибел) порядок фильтра N = 7. В среднем, при изменении N на единицу коэффициент подавления сигнала изменяется на 6 децибел.
Исходные требования к передаточной функции фильтра обычно задаются в виде значений ωp, ωs и коэффициентов неравномерности (пульсаций) A p и A s (см. рис. 3). Для определения частоты среза ωc по уровню 0,707 и порядка фильтра введем параметр ε (коэффициент пульсаций в полосе пропускания?), связанный с коэффициентом А р следующим соотношением:
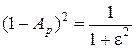 . .
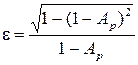 = = 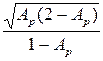 = = 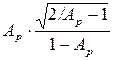 . .
| (1.3) |
Для учета деформации частотной шкалы в процессе билинейного преобразования при переходе в дальнейшем к полиномам по Z, выполняем расчет деформированных частот Ωp и Ωs по формулам:
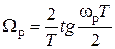 , ,
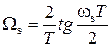 . .
| (1.4) |
При нормированной частоте W = ω/Ωc, где Ωc соответственно также деформированная частота, на границах переходной зоны выполняются равенства [4]*:
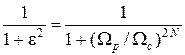 , ,
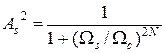 . .
| (1.5) |
Отсюда:
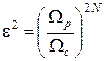 ,
, 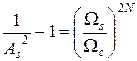 .
.
Решая эти два уравнения совместно, находим:
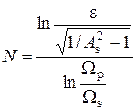 , ,
| (1.6) | |
| Ωc = Ωp / ε1/ N . | (1.7) |
1.4 Преобразование Лапласа
Переводим функцию | H (W)|2 на координатную ось пространства преобразования Лапласа при p = j W, для чего достаточно подставить W = p / j:
| |H(р)|2 = 1/[1+(p / j)2N]. | (1.8) |
Полюсы функции находятся в точках нулевых значений знаменателя:
1+(p / j)2N = 0, p = j 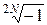 . .
| (1.9) |
Отсюда следует, что полюсы располагаются на единичной окружности в p -плоскости, а их местоположение определяется корнями уравнения (1.9). В полярных координатах:
| pn = j exp(j π(2 n –1)/2 N), n = 1,2,...,2 N. | (1.10) |
или
| pn = j cos[π (2 n –1)/2 N ] ‒ sin[π (2 n –1)/2 N ]. | (1.10') |
Как следует из формулы (1.10) и наглядно видно на рис. 1.2 примера, все полюса с n ³ N являются комплексно сопряженными с полюсами n < N. Значит, можно сказать, что квадрат передаточной функции включает в себя функцию (полином Баттерворта) B N(p) и ее комплексно-сопряженную. Т.е. (1.1) можно записать в виде
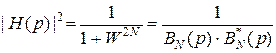 .
.
Таким образом, преобразование Лапласа передаточной функции
| H (p) = C / BN (p), | (1.11) |
где C - масштабный множитель, B (p) - полином Баттерворта.
При этом устойчивую минимально-фазовую передаточную функцию фильтра образуют полюса левой половины р -плоскости:
| B (p) = B 1(p) B 2(p)... B N(p), | (1.12) |
| Bn (p) = p - pn. | (1.13) |
Bn (p) – n -ый полином первой степени; pn – n -ый полюс.
Практическая реализация фильтра Баттерворта при четном значении N производится в виде последовательной каскадной схемы биквадратными блоками, т.е. составными фильтрами второго порядка. Для этого множители B (p) в (1.12) объединяются попарно с обоих концов ряда по n (от 1 до N) по комплексно сопряженным полюсам, при этом для каждой пары получаем вещественные квадратичные множители:
| В m(p) = B n(p)· B N+1–n(p) = = [ p + j exp(j π(2 n –1)/2 N)][ p + j exp(j π (2(N +1) –2 n –1)/2 N)] = = [ p + j exp(j π (2 n –1)/2 N)][ p - j exp(j π (2 n –1)/2 N)] = = p 2+2 p sin(π (2 m –1)/2 N)+1, n = 1,2,..., N /2; m = n. | (1.14) |
Общее количество секций фильтра M = N /2. При нечетном N к членам (1.14) добавляется один линейный множитель с вещественным полюсом p (N +1)/2 = ‒1, пример положения которого на р -плоскости можно видеть на рисунке 1.2 примера для N =5:
| В (N +1)/2(p)= p +1. | (1.15) |
Машинное время фильтрации на один оператор фильтра первого или второго порядка практически не отличаются, поэтому можно не рекомендовать использование операторов первого порядка и при установлении порядка фильтра по формуле (1.6) округлять расчетное значение N в сторону большего четного числа, что создает определенный запас по крутизне среза частотной характеристики.
Таким образом, передаточная функция ФНЧ Баттерворта в p -области при четном N:
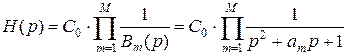 , ,
| (1.16) |
| a m = 2 sin(π(2 m -1)/2 N), m = 1,2,..., N /2. | (1.17) |
При нечетном N:
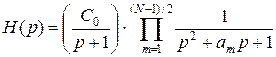 . .
| (1.16') |
1.5 Билинейное преобразование
Для перевода передаточной функции фильтра в z -область производится билинейное преобразование, для чего в выражение (1.16) подставляется параметр р:
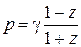 . .
| (1.18) |
С учетом автоматического возврата к нормальной шкале частот в главном частотном диапазоне z-преобразования значение коэффициента γ:
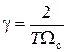 . .
| (1.19) |
После перехода в z-область и приведения уравнения передаточной функции в типовую форму, для четного N получаем передаточную функцию из М = N /2 биквадратных блоков:
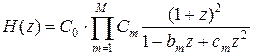 . .
| (1.20) | |
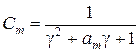 . .
| (1.21) | |
| b m = 2· C m (γ2 - 1). | (1.22) | |
| c m = C m (γ2 - a mγ + 1). | (1.23) |
При нечетном N добавляется один линейный блок первого порядка, который можно считать нулевым блоком фильтра (m =0):
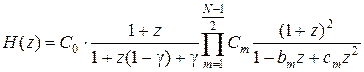 , ,
| (1.24) |
при этом, естественно, в выражении (1.24) используются значения коэффициентов C m, b m и c m, вычисленные по (1.21-1.23) для нечетного значения N.
Значение множителя C 0 в общем случае находится нормировкой к 1 коэффициента передачи фильтра при ω = 0. Для ФНЧ при использовании вышеприведенных формул значение C 0 равно 1.
При z =exp(- j ω) главный диапазон функций H(z) будет от –π до π. Для получения передаточной функции в шкале физических частот достаточно вместо z в выражения (1.20, 1.24) подставить значение z =e- j ω T, где T – шаг (период) дискретизации, и проверить соответствие расчетной передаточной функции заданным условиям.
Во временной области фильтрация выполняется последовательной сверткой входного сигнала с операторами ячеек фильтра:
| yk = xk * { h 0(i)} * h 1(i) * … * hМ (i), i = 0,1,2. |
Уравнение рекурсивной фильтрации для m -го оператора фильтра:
| yk = Cm (x k+2 x k-1+ x k-2) + bm y k-1 - cmy k-2. | (1.25) |
Уравнение рекурсивной фильтрации для дополнительного h 0(i) линейного оператора фильтра при нечетном N:
| y 0 = (xk + xk -1)/(γ +1) + yk -1·(γ -1)/(γ +1) | (1.26) |
4 Высокочастотный фильтр Баттерворта
2.1 Синтез фильтров методом частотного преобразования
Высокочастотные и полосовые фильтры конструируются путем частотной трансформации передаточных функций фильтров низких частот. Если обозначить аргумент передаточных функций ФНЧ через p = j W, a функций ФВЧ и ПФ через s= j w, то всегда можно найти такую функцию частотного преобразования p= F (s), которая превращает один тип фильтров в другой. Для преобразования ФНЧ → ФВЧ функция частотного преобразования имеет вид:
| p = 1/s, | (2.1) |
В этом нетрудно убедиться сравнением двух видов преобразования. Как известно, передаточная функция ФВЧ может быть получена из ФНЧ разностью между широкополосным (всепропускающим) фильтром (H (ω)=1) и ФНЧ. Применяя этот метод для функции Баттерворта, получаем:
| | H (w)|2 = 1-| H (W)|2 = 1- 1/(1+W2 N ) = W2 N /(1+W2 N ). | (2.2) |
С другой стороны, при W=p/ j из (1.1) получим:
| H (p)|2 =1/(1+(p/j)2 N ) = 1/(1-p2 N ).
Выполняя подстановку (2.1) в это выражение, получаем:
| H (s)|2 = s2 N /(s2 N -1).
Возвратимся из последнего выражения к аргументу w с учетом принятого равенства s= j w:
| | H (j w)|2 = (j w)2 N /((j w)2 N -1) =(w)2 N /(1+(w)2 N), | (2.2) |
что полностью повторяет (2.2) при w=W.
Подставляя p=1/s непосредственно в выражение H (p) (1.16) для четного значения N, получаем:
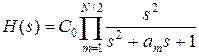 . .
| (2.3) |
Для нечетного N:
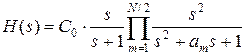 . .
| (2.4) |
После билинейного z -преобразования выражения с подстановкой s=γ(1-z)/(1+z), для четного и нечетного значений N соответственно:
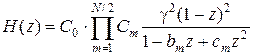 . .
| (2.5) | |
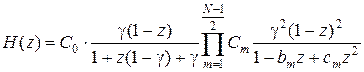 . .
| (2.6) | |
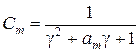 .
b m = 2· C m (γ2 - 1).
c m = C m (γ2 - a mγ + 1). .
b m = 2· C m (γ2 - 1).
c m = C m (γ2 - a mγ + 1).
| (2.7) |
Значения коэффициентов Cm, bm, cm остаются без изменения (сравнить с (1.21-1.23)). При задании частотных параметров ФВЧ в том же виде, что и для ФНЧ, формула расчетов N и Ωc получается аналогично ФНЧ, при этом в знаменателе выражения (1.6) отношение Ωp/Ωs заменяется на Ωs/Ωp:
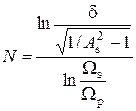 , ,
| (2.8) |
а в (1.7) деление членов правой части меняется на умножение:
| Ωc = Ωp·δ1/N. | (2.9) |
Уравнение рекурсивной фильтрации для m-го оператора фильтра:
| yk = γ2· Cm (xk - 2 xk -1+ xk -2) + bm yk -1 - cm yk -2. | (2.10) |
Уравнение рекурсивной фильтрации для дополнительного h0(i) линейного оператора фильтра при нечетном N:
| y 0 = γ ·(x k - xk -1)/(γ +1) + yk -1·(γ - 1)/(γ +1). | (2.11) |
5 Полосовой фильтр Баттерворта
Как известно, полосовой фильтр можно получить непосредственной комбинацией низкочастотного и высокочастотного фильтра при перекрытии полосы пропускания фильтров. Нормированное преобразование в этом случае имеет вид:
| p = s+1/s, | (3.1) |
где р - комплексная частота в уравнении фильтра низких частот; s - комплексная частота в уравнении полосового фильтра.
Подставив в (3.1) значения p = jW и s = jw, получим уравнение:
| W = [w2-1]/w, | (3.2) |
которое является квадратичным:
| w2-Ww-1 = 0. | (3.2) |
Корни уравнения (3.2):
(w)1,2 = W/2 ± 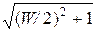 . .
| (3.3) |
5.1 Расщепление спектра.
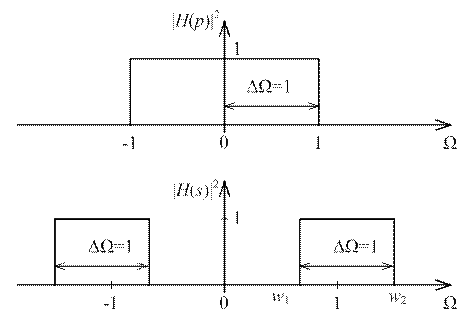
При W=0 имеем w =±1, т.е. центр полосы пропускания ФНЧ (от -Wc до +Wc) расщепляется на два (как и положено, для полосовых фильтров) и смещается в точки w =±1. Подставив в (3.3) граничную частоту Wс=1 нормированного ФНЧ, определяем граничные частоты нормированного полосового фильтра в виде пары сопряженных частот:
w1 = ±0.618, w2 = ±1.618
Сущность произведенного преобразования наглядно видна на рис. 3.1. Ширина полосы пропускания нормированного ПФ равна 1.
|
| Рисунок 3.1 – Расщепление полосы |
Полученное преобразование можно распространить на полосовой фильтр с ненормированными частотами ωн и ωв.
Введем понятие геометрической средней частоты фильтра ωо:
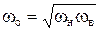 . .
| (3.4) |
Ширина полосы пропускания ПФ связана (см. рис.3.1) с граничной частотой ФНЧ соотношением:
Δω= ωв - ωн.
В долях средней геометрической частоты:
| Wн = (ωв - ωн)/ ωо = Wc. | (3.5) |
Заменяя в (3.4-3.5) значение ωв на произвольную частоту ω и подставляя в (3.5) значение ωн = ω·ωо2 из (3.4), получаем произвольную частоту W:
| W = (ω – ωн)/ ωо = ω/ωо - ωо / ω. | (3.6) |
Отсюда, в выражении (1.1) вместо нормированной частоты W = ω/ ωс можно применить функцию частоты полосового фильтра w(ω):
w(ω) = (ω2- ωо2)/[ ω (ωв - ωн)],
или, подставляя (3.4) вместо ωо:
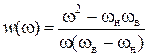 . .
| (3.7) |
Тем самым передаточная функция ФНЧ выражается в единицах, которые позволяют после применения преобразования (3.1) использовать для задания необходимые граничные частоты ωн и ωв полосового фильтра.
5.2 Полосовой фильтр на s-плоскости
С учетом деформации частот, принимаем p = j w = j (ω2- Ωн Ωв)/[ω (Ωв- Ωн)], s= j ω и заменяем ω = s/ j в выражении р:
| р = (s2+ Ωн Ωв)/[s(Ωв- Ωн)], s2-p(Ωв- Ωн)s+ Ωн Ωв = 0. | (3.8) |
Корни уравнения (3.8) определяют местоположение полюсов ПФ:
s = s* = p (Ωв- Ωн)/2 ± 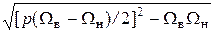 . .
| (3.9) |
Уравнение (3.9) показывает расщепление каждого p-полюса, определяемых выражением (1.14), на два комплексно сопряженных полюса s-плоскости, произведение которых будет давать вещественные биквадратные блоки в s-плоскости. При этом следует учесть то обстоятельство, что устойчивому рекурсивному фильтру на z-плоскости должны соответствовать полюса только одной (левой) половины p- и s - плоскостей.
5.3 Передаточная функция.
При применении преобразования (3.1) к передаточной функции в полиномиальной форме (1.11), получаем:
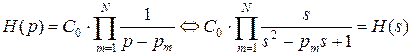 , ,
| (3.10) |
Выражение (3.10) не требует нахождения полюсов, т.к. они уже известны и определяются выражением (3.9). С учетом этого функция H (s) может быть записана с объединением в биквадратные блоки комплексно сопряженных полюсов с вещественными коэффициентами:
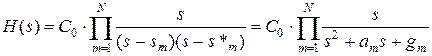 , ,
| (3.11) |
где значения аm и gm могут быть определены непосредственно по полюсам (3.9):
| a m = -2 Re sm, g m = (Re sm)2 + (Im sm)2 = |sm|2. | (3.12) |
При использовании ненормированных частот ω, достаточно существенных по своей величине, значения s-полюсов и, соответственно, величины коэффициентов аm и gm могут иметь большие порядки (как видно из примера проектирования данного типа фильтра), что нежелательно для дальнейших расчетов и может приводить к появлению погрешностей при ограничении разрядности. Для исключения этого фактора значения полюсов sn рекомендуется нормировать на среднюю геометрическую частоту:
| sn = sn/ωo. | (3.12) |
Коэффициент γ билинейного преобразования для ненормированных значений ω и полюсов s n имеет классическую форму: γ = 2/ T. Соответственно, для нормированных значений:
| γ = 2/(T ·ωo). | (3.13) |
После билинейного z-преобразования выражения (3.11), получаем:
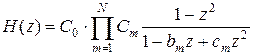 . .
| (3.13) | |
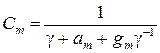 . .
| (3.14) | |
| bm = 2 Cm (γ – gm γ –1). | (3.15) | |
| cm = Cm (γ – am + gm γ –1). | (3.16) |
Нормировкой H (z) к 1 на геометрической средней частоте фильтра определяют общий множитель C:
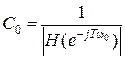 . .
| (3.17) |
6 Заграждающий фильтр Баттерворта
Если применить обратное частотное преобразование 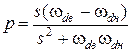 p=s(ωв–ωн)/(s2+ωвωн), то в результате будет получен полосовой заградительный фильтр.
p=s(ωв–ωн)/(s2+ωвωн), то в результате будет получен полосовой заградительный фильтр.
7 Фильтры Чебышева
В большинстве применений самым существенным обстоятельством является то, что неравномерность характеристики в полосе пропускания не должна превышать некоторой величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность характеристики по всей полосе пропускания, но при этом сильно увеличивается острота её излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания, получаем более острый излом. Амплитудная характеристика этого фильтра описывается уравнением:
, 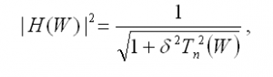
где TN – полином Чебышева первого рода степени N, а δ – константа, определяющая неравномерность характеристики в полосе её пропускания.
На самом деле фильтр Баттерворта с максимально плоской характеристикой в полосе пропускания не так привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью характеристики в полосе пропускания (для фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте ωc, а для фильтра Чебышева — пульсации, распределенные по всей полосе пропускания). Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от расчетной, а это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания.
В свете вышеизложенного, весьма рациональной структурой является фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что в полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1 дБ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием на частоте, отличающейся на 25% от граничной частоты пропускания. Расчет показывает, что в этом случае требуется 19-полюсной фильтр Баттерворта или всего лишь 8-полюсный фильтр Чебышева.
7.1 Фильтры первого рода.
Фильтры Чебышева с пульсациями передаточной функции в полосе пропускания и гладким затуханием в полосе подавления называют фильтрами Чебышева первого рода, в отличие от инверсных фильтров Чебышева (второго рода). Аппроксимационная формула фильтров Чебышева первого рода определяется выражением:
| | H (W)|2 = 1/ [1+δ2 T N 2(W)], | (5.1) |
где Т N(W) - многочлен Чебышева N -го порядка:
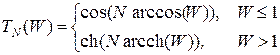 . .
| (5.2) |
N – порядок фильтра, определяющий крутизну среза АЧХ;
δ – параметр, характеризующий пульсации в полосе пропускания (коэффициент пульсаций в полосе пропускания).
Критерий приближения Чебышева, который широко используется не только в теории фильтров - минимум максимальной ошибки приближения (минимаксное приближение). В соответствии с этим приближением параметры передаточной функции подбираются таким образом, чтобы в полосе передачи АЧХ наблюдались равноволновые пульсации коэффициента передачи, которые являются "платой" за повышение крутизны среза фильтра.
Полиномы Чебышева вычисляются по рекуррентной формуле:
| TN (W) = 2W TN -1(W) - TN -2(W), T 1(W) = W, T 0(W) = 1. | (5.3) |
Для ФНЧ при W = ω/ωp имеет место ТN (1) = 1, | H (W)|2 = 1/(1+δ2). При задании полосы по уровню А p значение δ рассчитывается аналогично фильтру Баттерворта по (1.3).
Соответственно, при задании Аs на границе полосы подавления, имеем [4]:
| 1/(1+δ2 TN 2(Ωs/ Ωp)) = A s2. | (5.4) | |
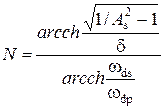 . .
| (5.5) |
Дальнейшие расчеты идентичны расчетам фильтров Баттерворта, равно как и частотные преобразования фильтров ФНЧ в ФВЧ и ПФ.
7.2 Фильтры второго рода
Для фильтров Чебышева второго рода, с гладкой передаточной характеристикой в зоне пропускания и равноволновыми пульсациями в зоне подавления, используется функция:
| | H (W)|2 = 1/[1+δ2(TN 2(Ws)/ TN 2(Ws/W))], | (5.6) |
где W = ω/ωp, Ws = ωs/ωp. Условие задания параметра δ остается без изменений. На границе полосы подавления при ω = ωs: 1+δ2 TN 2(ωs/ ωp) = 1/ A s2, откуда значение N также определяется аналогично фильтру первого рода. Дальнейший порядок расчетов фильтров Чебышева второго рода не отличается от фильтров первого рода.
Порядок выполнения работы
Данная работа выполняется на ПЭВМ с использованием программы MathCAD. Используя исходные данные, полученные от преподавателя, спроектировать НРФ четырех типов: ФНЧ, ФВЧ, ПФ, ЗФ. Для этого:
- выбрать подходящую оконную функцию
- определить и построить идеальную импульсную характеристику
- реальную импульсную характеристику
- построить временную характеристику окна.
- АЧХ синтезированного фильтра
Синтез ФНЧ Баттерворта
Расчет дополнительных параметров:
1. Рассчитать значение d по формуле (1.3).
2. Деформированные частоты по формуле (1.4).
3. Определить порядок фильтра по формуле (1.6).
4. Определить частоту среза по формуле (1.7).
5. По формуле H (w)= [1/(1+w2 N )]1/2, w = ω/Ωc, построить графики передаточных функций.
6. Вычисляем значения полюсов фильтра по формуле (1.10). Построить на графике значения полюсов на р-плоскости.
7. Вычисляем значения коэффициентов a m по формуле (1.17).
8. Вычисляем значение коэффициентоа g по формуле (1.19).
9. Вычисляем значения коэффициентов Cm, bm и cm по формулам (1.21) – (1.23).
10. Подставляем вычисленные коэффициенты в выражения (1.20) для четного или (1.24) для нечетного порядка N. Вычисляем значения передаточных функций при z = exp(- j wD t). Построить графики полученных функций.
11. Построить график каждого оператора фильтра.
12. Для оценки длительности импульсной реакции фильтра вычислить и построить импульсную реакцию фильтра по формуле (1.25) при подаче на вход фильтра единичного импульса.
Синтез ФВЧ Баттерворта.
Расчет дополнительных параметров:
1. Рассчитать значение d по формуле (1.3).
2. Определить деформированные частоты по формуле (1.4).
3. Рассчитать порядок фильтра по формуле (2.8).
4. Рассчитать частоту среза фильтра по формуле (2.9).
5. Построить график функции H (w), w = ω/Ωc.
6. Т.к. полюса pn фильтра полностью повторяют полюса ФНЧ, соответственно, повторяются и значения коэффициентов a m. Вычисляем значения коэффициентов a m по формуле (1.17).
7. Вычисляем остальные коэффициенты: g по формуле (1.19), Cm, bm и cm по формулам (2.7).
8. Подставляем вычисленные коэффициенты в выражения (2.5) для четного или (2.6) для нечетного порядка N. Вычисляем значения передаточных функций при z = exp(- j wD t). Построить графики полученных функций.
9. Вычислить и построить импульсную реакцию фильтра по формуле (2.10) при подаче на вход фильтра единичного импульса.
Оформление отчета
В отчете необходимо представить результаты работы.
Список литературы
7. Бондарев В.Н., Трёстер Г., Чернега В.С. Цифровая обработка сигналов: методы и средства. Учеб. пособие для вузов. – 2-е изд. – Х.: Конус, 2001. –398 с.
8. Глинченко А.С. Цифровая обработка сигналов: В 2 ч. Ч. 1. Красноярск: Изд-во КГТУ. 2001. – 199 с.
9. Давыдов А.В. Цифровая обработка сигналов: Тематические лекции. – Екатеринбург: УГГУ, ИГиГ, ГИН, Фонд электронных документов, 2005.
10. Хэмминг Р. У. Цифровые фильтры. – М.:Советское радио. 1980. – 224 с.
11. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М: Мир, 1978.
Айфичер, Эммануил С., Джервис, Барри У. Цифровая обработка сиrналов: практический подход, 2-е издание.: Пер. с анrл. М.: Издательский дом "Вильяме", 2004. – 992 с.
Date: 2016-05-23; view: 3290; Нарушение авторских прав