Лабораторная работа №1. Использование дискретного преобразования Фурье для фильтрации сигнала

О.О. Щелконогов

МЕТОДИЧНІ ВКАЗІВКИ
до лабораторних робіт з курсу
"Цифрова обробка сигналів"

Частина 1

під загальною редакцією проф.В.С. Блінцова

Миколаїв 2012

Содержание

О.О. Щелконогов. 1

МЕТОДИЧНІ ВКАЗІВКИ до лабораторних робіт з курсу "Цифрова обробка сигналів" 1

Содержание. 2

Лабораторная работа №1. Использование дискретного преобразования Фурье для фильтрации сигнала. 3

Лабораторная работа №2. Быстрое преобразование Фурье. 10

Лабораторная работа №3. Дискретное косинусное преобразование (ДКП) 23

Лабораторная работа №4. Дискретная свертка и фильтрация сигнала. 29

Лабораторная работа №5. Синтез нерекурсивных цифровых фильтров (методом окон) 42

Лабораторная работа №6. Синтез рекурсивных цифровых фильтров. 85

Лабораторная работа №7. Обработка изображений. 118

Часть 1. Анализ и поэлементная обработка изображений. 118

Часть 2. Локальная фильтрация изображений. 131

Лабораторная работа №1. Использование дискретного преобразования Фурье для фильтрации сигнала

Цель работы: Изучение дискретного преобразования Фурье (ПФ) и его использования для обработки сигнала в частотной области.

Необходимые теоретические сведения

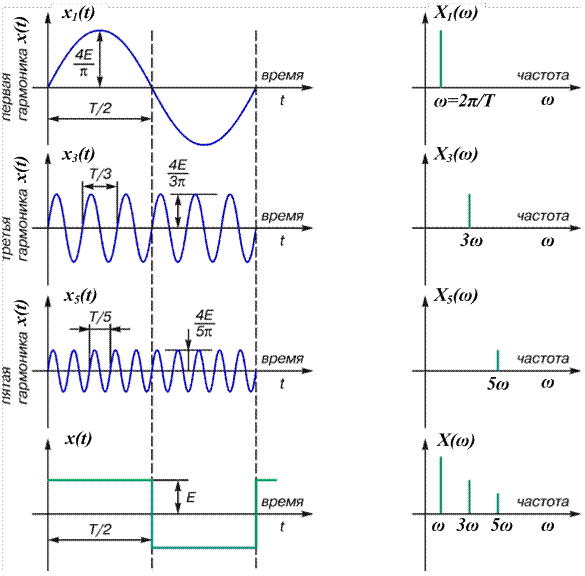
В основе преобразования Фурье (ПФ) лежит следующая идея: почти любую периодическую функцию можно представить суммой отдельных гармонических составляющих (или проще – гармоник т.е. синусоид и косинусоид с различными амплитудами A, периодами Т и, следовательно, частотами ω). Пример одной из таких функций x (t), состоящей из гармоник x_i (t), приведен на рис. 1.

Рис. 1. Представление прямоугольного импульса суммой гармоник

Понятия «изобразить в частотной области некую функцию от времени» и «нарисовать спектр этой функции» – равнозначны. Если посмотреть на рис.1 по горизонтали слева направо, то совершится переход от какой-либо функции времени к ее спектру – благодаря ПФ. А нижняя часть рисунка показывает один из основных принципов ПФ – спектр суммарной функции времени равен сумме спектров ее гармонических составляющих.

Достоинством ПФ является его гибкость – преобразование может использоваться как для непрерывных функций времени, так и для дискретных.

Если сигнал имеет аналоговый вид – представляет собой непрерывную функцию, определенную на бесконечном промежутке времени, то преобразование Фурье производится по следующим формулам (первая формула для прямого преобразования Фурье, вторая – для обратного):

;

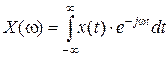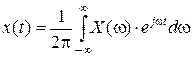
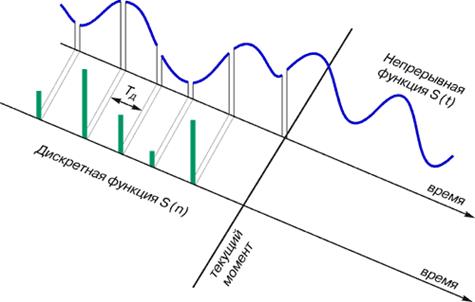
Для получения дискретной функции времени надо подвергнуть процессу дискретизации непрерывную функцию времени. Это изображено на рис.2.

Рис. 2. Дискретное представление непрерывной функции

Период одного цикла его работы T _д (или T ₀, или ∆ t) называется «периодом дискретизации», или «шагом дискретизации». Устройства, в которых осуществляется такая операция, называются аналого-цифровые преобразователи (АЦП). Необходимо иметь в виду, что перед тем, как подавать аналоговый сигнал на вход АЦП, его предварительно пропускают через аналоговый фильтр. Это делают для того, чтобы при дискретизации выполнялось требование теоремы Котельникова (для случая равномерной дискретизации с использованием частотного критерия Котельникова).

Для дискретного сигнала, представляющего собой решетчатую функцию и, как правило, определенного на конечном промежутке времени (времени измерения) преобразование Фурье принимает вид так называемого дискретного преобразования Фурье (ДПФ):

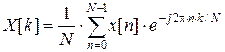
		(1)
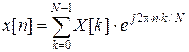
		(2)

где: T – период дискретизации; n – номер отсчета дискретизированного сигнала, n =0,1,2,…, N –1; k – номер гармоники сигнала, k =0,1,2,…, N –1, частота гармоник равна k / T _изм, где T _изм– период измерения; j – мнимая единица.

Если ввести вспомогательную функцию 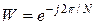, то выражения 1 и 2 можно записать в виде

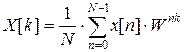
		(3)
		(4)

Принято в цифровой обработке в виде x [ n ] обозначать исходную функцию (не обязательно это должна быть функция времени, цифровой сигнал лишен своей физической природы); в виде X [ k ] обозначать результат преобразования (в данном случае - преобразования Фурье) исходной дискретной функции x [ n ]. Достоинством дискретного преобразования Фурье является то, что результат преобразования X [ k ] подразумевает некий физический смысл (представление сигнала в частотной области, спектр сигнала), в отличие от других преобразований, которые просто переводят исходную функцию в некую область, в которой удобнее выполнять те или иные преобразования.

Дискретное преобразование Фурье может эффективно использоваться для очистки сигналов от помех. Для этого «зашумленный» сигнал переводится в частотную область и, используя те или иные критерии, производится удаление помех (например, удаляются гармоники выше некоторой). Затем сигнал переводится обратно во временную область с использованием обратного преобразования Фурье.

Указания к выполнению работы

Данная работа выполняется на ПЭВМ с использованием программы MathCAD 2001. Встроенные в систему MathCAD средства быстрого преобразования Фурье (БПФ) существенно упрощают процедуру приближенного спектрального анализа. БПФ – быстрый алгоритм переноса сведений о функции, заданной 2 ⁿ отсчетами во временной области, в частотную область. Если речь идет о спектральном анализе функции x [ n ], заданной действительными отсчетами, то следует использовать функцию FFT (x), где x – вектор, элементы которого хранят отсчеты функции x [ n ]. Результатом будет вектор X с комплексными элементами – отсчетами в частотной области (MathCAD выдает их вдвое меньше, чем отсчетов во временной области, т.к. вторая половина зеркально повторяет первую).

Порядок выполнения работы

Каждая бригада получает свой файл, содержащий оцифрованный сигнал с помехами (шумом). Задачей студентов является очистка сигнала от шума. Смысл преобразования заключается в выделении определенной части спектра сигнала (частотная область) путем отсечения гармоник с малой амплитудой (помеха) и его обратном преобразовании во временную область.

1. Считать с диска отсчеты непрерывного сигнала x (t), дискретизированного с некоторым постоянным шагом, т.е. дискретный сигнал x [ n ]. Для этого Можно использовать метод ввода из текстового файла, особенно в случае, когда число значений входного сигнала неизвестно.

Кликнуть правой кнопкой мыши и в контестном меню выбрать Вставить -> Ввод из файла… Выбрать в окне Формат файла – Текст и через кнопку Обзор… указать путь к фалу. Флаг Запятая как десятичный разделитель должен быть снят. Нажать кнопку Готово. После вывода на экран значка файла с путем указать имя входного массива.

С использованием панели инструментов Матрица транспонировать входной массив.

С помощью функции last(имя_транспонированного_ассива) получить номер последнего элемента массива. Т.к. отсчет номеров элементов идет с нуля, число элементов будет на 1 больше, чем номер последнего элемента.

2. Чтобы вывести на экран результат считывания (массив x), достаточно записать x =<Вычислить>.

3. Выведите график полученного сигнала, для чего выполните: меню Вставка > График > X-Y зависимость, где по горизонтальной оси расположить номера отсчетов – n, а по вертикальной – значения измеренного сигнала x_n. Т.к. сигнал дискретный, необходимо представит его в соответствующем виде: двойной клик мыши на графике – вкладка След – Тип указать вместо lines параметр stem. Обратите внимания на вид графика.

4. Используя формулу (1), приведенную в теоретической части, выполнить прямое преобразование Фурье и определить коэффициенты ряда Фурье X_k. При этом не забыть вначале определить переменную k, как это было сделано для переменной n в п.1.

5. Чтобы вывести на экран таблицу результатов расчета X, достаточно записать X =<Вычислить>.

6. Построить график полученного образа сигнала в частотной области (спектр сигнала). Т.к. найденные значения будут комплексными, использовать модуль | X_k |. Приведите зависимость | X_k | к дискретному виду (stem) как в п.3.

7. Выполнить обратное преобразование Фурье по формуле (2) (восстановить сигнал). Чтобы полученные значения не заменили значения исходного сигнала, для выходного массива вместо имени x необходимо использовать другое имя, например, xrev.

8. Построить график восстановленного сигнала и сравнить полученный результат с исходным сигналом x _n. Для этого на вертикальной оси после имени значений восстановленного сигнала xrev _n через запятую указать имя значений исходного сигнала x _n.

9. Используя встроенную в MathCAD функцию FFT, найти преобразование Фурье Y:= FFT(x) средствами MathCAD. Число спектральных коэффициентов, которое выдает MathCAD, будет половина плюс одно от числа исходных отсчетов во временной области (N /2)+1, в силу периодичности спектра. Вторая половина коэффициентов Фурье – зеркальное отображение первой и это половина следующего периода спектра. Получить номер последнего частотного коэффициента можно с помощью функции last(Y), которая вернет номер последнего значения L:

L:=last(Y)

L =<Вычислить>

10. Построить график, на котором должны быть результаты вычисления | X_l | по (1) и | Y_l | по встроенной функции FFT, где l:=0.. L. Для этого у вертикальной оси записать через запятую | X_l | и | Y_l |. Привести зависимости к дискретному виду.

11. Сравнить полученный результат. При совпадении можно сделать вывод о правильности выполнения операций.

12. Изучите сигнал в частотной области. Попытайтесь определить, что является помехой, а что – полезным сигналом. Отфильтруйте сигнал путем «вырезания» гармоник исходного сигнала (т.е. путем приравнивания их нулю) меньших по амплитуде, чем некоторое пороговое значение p, ниже которого сигнал считается шумом. Пример процедуры фильтрации (в данном случае порог имеет значение 1, но у каждого он свой):

p:=1

В качестве индекс следует использовать переменную k, если в п. 14 для восстановления сигнала будет использоваться формула (2) или l, если будет использоваться встроенная функция IFFT. Эта последовательность операторов интуитивно понятна: XC_i = X_i, если X_i > p и XC_i = 0, если это не так.

13. Построить график «очищенного» сигнала XC в частотной области.

14. Выполнить обратное дискретное преобразование Фурье для XC и построить график очищенного сигнала во временной области xc. Для удобства восприятия очищенный сигнал на графике следует представить не в виде stem, а в виде lines.

Оформление отчета

В отчете необходимо представить все этапы выполнения работы, снабдив их текстовыми комментариями к каждой выполняемой операции и графиками, поясняющими суть выполнения операций.

Вопросы к лабораторной работе

1. Что такое гармоника (гармоническая составляющая)?

2. Какой вид имеет синусоида в частотной области?

3. Что осуществляет прямое преобразование Фурье?

4. Какой вид имеет дискретная функция?

5. Что такое дискретизация?

6. Какой вид имеют формулы прямого и обратного дискретного преобразования Фурье?

7. Для чего перед дискретизацией аналоговый сигнал пропускают через аналоговый фильтр?

8. Сформулируйте теорему Котельникова.

9. Из каких этапов состоит фильтрация, описанная в работе?

Date: 2016-05-23; view: 1942; Нарушение авторских прав