
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 3. Организация управления корпоративными финансами на основе критерия стоимости 3 page
|
|
- в процессе оценки денежных потоков финансовый менеджер оперирует не учетными, а финансовыми категориями (потоками денежных средств);
- информация о денежных потоках должна быть представлена в форме разностей между показателями денежных потоков с учетом и без учета реализации проекта (значение имеет лишь прирост денежных средств в результате реализации проекта);
- чистые денежные потоки от реализации проекта рассчитываются лишь по результатам операционной деятельности, и не учитывают процентные платежи, платежи в погашение кредитов или выплату дивидендов[46]. Стоимость (цена) финансовых ресурсов, с учетом эффекта налогового корректора, отражается в ставке дисконтирования;
- прошлые (невозмещаемые) затраты на проект (" sunk costs ") игнорируются;
- проекты, связанные с выходом на рынок с новой продукцией, с использованием новых каналов распределения продукции и т.п. должны сопровождаться анализом возможности возникновения эффекта " каннибализации ", то есть "поеданием" новой продукцией или новыми каналами распределения части уже принадлежащего данной фирме рынка[47]. При обнаружении подобного эффекта его последствия должны быть оценены в стоимостном выражении и учтены в качестве оттоков денежных средств;
- должны быть выявлены и, несмотря на свой неденежный характер, учтены в качестве оттоков издержки упущенных возможностей, возникающие при существовании возможностей альтернативного использования тех или иных материальных и нематериальных активов, предполагаемых к использованию в проекте (альтернативные издержки использования финансовых ресурсов отражены в стоимости капитала);
- амортизация учитывается лишь в расчете налоговых платежей, и не учитывается в расчете денежных оттоков;
- если проект по своему содержанию носит стратегический характер и его осуществление сопровождается образованием долгосрочных нематериальных активов типа гудвилла, устойчивой репутации в глазах потребителей и т.п., то ликвидационная стоимость проекта обычно рассматривается как бессрочный или долгосрочный аннуитет с денежным потоком, равным денежному потоку за последний год срока экономической жизни проекта;
- если проект по своему содержанию не носит стратегического характера (например, обычная замена оборудования), то по окончании реализации проекта использованные долгосрочные активы могут быть реализованы по стоимости выше или ниже остаточной. В первом случае возникают дополнительные обязательства по налогу на прибыль, во втором – эффект «налогового прикрытия»: предполагается, что убыток от реализации уменьшит налогооблагаемую прибыль за соответствующий год;
- если проект предполагает дополнительные инвестиции в оборотный капитал (увеличение необходимых остатков денежных средств, прирост дебиторской задолженности, запасов и др.), то необходимо сделать предположение об уровне высвобождения инвестированных средств после окончания реализации проекта.
Основные критерии отбора инвестиционных проектов. Преимущества и недостатки этих методов. Сравнение методов расчета чистой приведенной стоимости и внутренней нормы доходности
К настоящему времени мировая практика управления финансами наработала целый спектр методов оценки инвестиционных проектов, базирующихся на различных предположениях и алгоритмах расчета. Сформировался объемный пласт научной, учебной и методической литературы, посвященной методам проектного анализа. Представленный ниже материал можно охарактеризовать лишь как экскурс в эту область, имеющий целью формирование у читателя объема знаний и навыков, достаточного для оценки инвестиционных проектов в наиболее распространенных на практике случаях.
Наиболее корректными с финансовой точки зрения, и поэтому рекомендуемыми к применению являются методы, основанные на дисконтировании чистых денежных потоков от реализации проекта. Указанные методы базируется исключительно на использовании сложных процентов с периодом начисления, равным периодичности денежных потоков по проекту[48]. При этом неявно используется предположение о реинвестировании полученного дохода под ставку доходности, равную ставке дисконтирования. Предполагается также, что ожидаемая доходность не меняется в течение всего периода выплаты доходов[49].
1. Метод расчета чистой приведенной (дисконтированной) стоимости (ценности) проекта (NPV – Net Present Value) основан на дисконтировании ожидаемых чистых денежных потоков от реализации проекта – CFi по ставке ожидаемой (необходимой) доходности на инвестированный капитал, или, что то же самое, средневзвешенной стоимости капитала фирмы r. Само значение NPV представляется в виде:
NPV = - I + CF1 / (1+r) + CF2 / (1+r) 2 + … + CFn / (1+r) n, (4.1)
где n – продолжительность экономической жизни проекта (как правило, в годах), I – необходимые первоначальные инвестиции в проект. Критерием того, должен ли быть проект принят или отвергнут, служит выполнение следующих неравенств:
NPV > 0 – проект принимается,
NPV < 0 – проект отвергается.
2. Метод расчета внутренней нормы доходности (IRR – Internal Rate of Return) основан на сравнении значения ставки дисконтирования, при которой NPV проекта равен нулю, со стоимостью капитала предприятия. Подставляя в формулу (4.1) вместо ставки r величину IRR, и приравнивая NPV нулю, получаем уравнение для определения IRR
NPV = - I + CF1 / (1+ IRR) + CF2 / (1+ IRR) 2 + …+ CFn / (1+ IRR) n = 0 (4.2)
Уравнение (4.2) является уравнением n- ной степени, которое, вообще говоря, может иметь n действительных корней. Однако, в соответствии с теоремой Декарта, если коэффициенты этого уравнения меняют знак один раз, уравнение имеет единственный положительный корень. Таким образом, если денежные потоки CFi положительны, уравнение (4.2) имеет единственный положительный корень (отрицательные корни финансового смысла не имеют). В противном случае мы имеем дело с множественностью положительных корней, что делает рассматриваемую методику оценки в такой ситуации неприменимой. На практике для решения уравнения (4.2) удобно использовать специальные финансовые калькуляторы или программные продукты.
Критерием принятия или непринятия проекта выступают следующие неравенства:
IRR > СС – проект принимается,
IRR < СС – проект отвергается,
где CC – стоимость капитала фирмы.
3. Близким по смыслу к методу расчета чистой приведенной стоимости является расчет индекса доходности (PI – Profitability Index). Индекс доходности записывается в виде:
PI = [ ∑СFi/(1+r)i ]: I, (4.3)
где суммирование осуществляет от 1 до n.
Критерием отбора проектов служит выполнение неравенства
PI > 1 – проект принимается,
PI < 1 – проект отвергается.
4. Метод расчета периода (срока) окупаемости инвестиций (PI – Payback Period) является одним из наиболее широко распространенных в мировой и отечественной практике благодаря своей простоте и наглядности. Период окупаемости инвестиций представляет собой продолжительность периода времени, в течение которого недисконтированные денежные поступления от реализации проекта превысят недисконтированные инвестиции в проект. Иными словами, это число лет, необходимых для возмещения стартовых инвестиционных расходов. Если в результате расчетов получается дробное число лет, то его, как правило, округляют до ближайшего большего целого. В отечественной практике данный метод является особенно популярным, так как высокий уровень рисков снижает удельный вес денежных потоков, которые ожидаются после достижения срока окупаемости проекта.
Отметим, что перечисленные методы отнюдь не исчерпывают весь спектр аналитических процедур, имеющийся в распоряжении финансового аналитика. В частности, существует несколько версий расчета так называемой модифицированной внутренней доходности (учитывающей реинвестирование получаемого дохода не по ставке доходности проекта, а по стоимости капитала); существуют различные варианты расчета срока окупаемости, в частности, на основе использования дисконтированных денежных потоков; в некоторых случаях может быть использована дисконтированная стоимость ожидаемых издержек. Обзор всех существующих методик выходит за пределы базового курса и является предметом рассмотрения специальной литературы.
С финансовой точки зрения наиболее корректным является метод расчета чистой приведенной стоимости (NPV). В отличие от метода расчета внутренней нормы доходности (IRR), который в случае меняющих более одного раза знак денежных потоков[50] может приводить к множественным положительным значениям IRR, метод расчета NPV применим к любым денежным потокам. Кроме того, оба указанных метода гарантированно ведут к одному решению, лишь если речь идет о принятии или непринятии единичного проекта. Если же рассматриваются два взаимоисключающих проекта, то эти методы могут дать противоположные результаты. В таком случае следует ориентироваться на метод расчета NPV. Тем не менее, характерное для расчета IRR представление результата в процентной, а не абсолютной форме представляется более привлекательным для большинства менеджеров, избавляя их от необходимости иметь точную оценку стоимости капитала – для сравнения достаточно и "грубой" оценки. Кроме того, использование относительного показателя – IRR позволяет получить информацию о «запасе финансовой прочности» проекта на случай, если фактические денежные поступления от проекта окажутся ниже прогнозных.
Остальные методы при всей своей простоте и наглядности страдают весьма существенным недостатком – игнорируют временную стоимость денег. К тому же учетные характеристики могут существенно отличаться от денежных, а показатель срока окупаемости инвестиций игнорирует доходы, которые будут получены после того, как проект «окупится». Кроме того, проект может иметь удовлетворительный срок окупаемости даже при нулевых значениях IRR!
На основании изложенных соображений можно сделать вывод о том, что различные методы анализа могут нести в себе различные аспекты информации об инвестиционной привлекательности проекта и, как таковые, должны использоваться в комплексе. В частности, завышенные значения чистых денежных потоков, не выявляемые на основе расчета и анализа NPV, могут проявить себя при анализе внутренней нормы доходности, если последняя принимает значения, не поддающиеся рациональному объяснению.
Анализ взаимоисключающих (альтернативных) проектов
Как уже отмечалось выше, использование методов расчета NPV и IRR для единичных проектов всегда ведет к одному и тому же результату с точки зрения выбора «принять – отвергнуть». Однако практика инвестиционного анализа достаточно часто сталкивается со случаями, когда проекты являются взаимоисключающими (или альтернативными). Примерами подобных ситуаций могут служить проект постройки гостиницы либо офисного комплекса на одном и том же участке земли, выбор между покупкой и лизингом объекта основных средств, размещение производственного предприятия возле основных источников сырья или рынка сбыта и т.п. Возникающая в таком случае проблема может быть проиллюстрирована следующим примером:
Пример. Взаимоисключающие проекты А и В характеризуются следующими денежными потоками:
Проект А: -50; 20; 20; 20; 20; 20
Проект В: -50; 5; 10; 20; 30; 60
При ставке дисконтирования 15% NPV проекта А составит 17.0; NPV проекта В составит 22.0. Внутренние нормы доходности проектов соответственно составят IRRA=28.65%;IRRB=26.72%. Таким образом, если руководствоваться методом расчета NPV, то предпочтительнее выглядит проект В, в то время, как руководствуясь критерием расчета IRR, можно прийти к выводу о предпочтительности проекта А. Противоположный порядок ранжирования проектов по степени их привлекательности объясняется неявным предположением о ставке реинвестирования денежных потоков, генерируемых проектами. Если при расчете NPV проектов средства реинвестируются под ставку дисконтирования, равную стоимости капитала (15% в нашем случае), то расчет внутренней нормы доходности IRR предусматривает реинвестирование под эту же ставку доходности (в нашем случае соответственно 28.65% и 26.72%). Легко заметить, что при стоимости капитала (или, что то же самое, средней доходности на один рубль вложенных средств) в 15% годовых у предприятия не возникнет проблем с реинвестированием средств под эту ставку[51]. Иное дело реинвестирование под более высокую ставку, равную IRR: весьма маловероятно, что проект потребует дополнительных инвестиций, совпадающих по величине и времени с поступлениями от реализации этого проекта. Более того, средневзвешенная стоимость капитала в 15% годовых делает привлечение дополнительных финансовых ресурсов под эту ставку заведомо более привлекательным, чем реинвестирование средств стоимостью в 28.65% или 26.72% годовых. Как следствие, именно критерий расчета чистой приведенной стоимости проекта дает однозначно верное ранжирование проектов.
В рассмотренном конкретном примере противоречивые результаты применения методов расчета IRR и NPV обусловлены различием в интенсивности притоков денежных средств. Вычитая денежные потоки проекта А из денежных потоков проекта В мы получим приростные денежные потоки, формирующие проект, имеющий положительный NPV[52]. Выбор проекта А означал бы игнорирование проекта с положительным NPV, что было бы неверным с точки зрения основополагающей цели финансового менеджмента – максимизации стоимости фирмы.
Приведенные выше рассуждения могут быть проиллюстрированы следующим рисунком:

Рис.4.1. Зависимость NPV от ставки дисконтирования для двух взаимоисключающих проектов А и В.
Графики зависимости NPV проектов А и В от величины ставки дисконтирования пересекают горизонтальную ось в точках 28.65% и 26.72%, которые соответствуют значениям их внутренней нормы доходности. Пересечению этих кривых между собой соответствует точка 22.56%. Пересечение с вертикальной осью имеет место при нулевой ставке дисконтирования, что означает сумму недисконтированных денежных потоков от реализации проекта, уменьшенную на величину первоначальной инвестиции в проект.
Как следует из рисунка, при значениях ставки дисконтирования, меньших 22.56% проект В более привлекателен, по сравнению с проектом А. Картина меняется на прямо противоположную, когда ставка дисконтирования становится выше 22.56%, причем при ставках, превышающих 26.72% приемлем только проект А. Если ставка дисконтирования выше 28.65%, оба рассматриваемых проекта будут неприемлемы (NPV<0).
Помимо интенсивности притоков денежных средств, на степень привлекательности инвестиционного проекта может существенным образом повлиять масштаб инвестирования: на практике совершенно необязательно, чтобы взаимоисключающие проекты предусматривали одинаковый начальный объем инвестиций. Более того, вероятнее всего первоначальные вложения в такие проекты будут различаться, иногда весьма значительно. Если эти различия в масштабе инвестирования во внимание не принимать, то 100% дохода на 1 рубль будут выглядеть предпочтительнее 20% на 100 руб. (напомним, что проекты взаимоисключающие!) Как и выше, не составит труда показать, на основе дисконтирования приростных денежных потоков, что использование критерия расчета внутренней нормы доходности и в этом случае может привести к игнорированию дополнительного проекта с положительным NPV. Следовательно, метод расчета NPV и здесь предпочтителен: чистая приведенная стоимость тем выше, чем больше масштаб инвестирования.
В заключение необходимо отметить, что метод расчета модифицированной внутренней нормы доходности (MIRR) свободен от описанного недостатка; однако расчет соответствующего показателя представляет собой достаточно громоздкую процедуру.
Анализ проектов различной продолжительности
В практике управления финансами вполне реальной представляется ситуация, когда аналитику необходимо сравнить инвестиционную привлекательность проектов различной продолжительности. Несмотря на техническую простоту изложенного ниже подхода, в теоретическом плане он далеко небезупречен и может быть применен только при выполнении достаточно жестких допущений. Речь идет о предположении о возможности повторения проекта конечное или бесконечное[53] число раз. Некоторые специалисты считают подобное предположение нереалистичным, и рекомендуют отдавать предпочтение проекту с более высоким значением NPVневзирая на сроки его осуществления[54]. С другой стороны, если различия в продолжительности осуществления проектов существенны, вполне реалистичным может оказаться предположение о повторном инвестировании средств в аналогичные проекты.
В качестве наиболее часто рекомендуемого рассмотрим метод цепного повтора проектов в рамках их общего срока действия. Этот метод предусматривает определение наименьшего срока, в течение которого каждый из анализируемых проектов может быть повторен целое число раз. Технически это сводится к определению наименьшего общего кратного чисел, представляющих собой продолжительности проектов в годах. Сравнение значений NPV каждого из проектов в пределах общего срока действия и позволит выявить предпочтительный.
Пример. При ставке дисконтирования 25% необходимо выбрать предпочтительный проект из двух альтернативных, характеризующихся следующими денежными потоками:
Проект А: -550, 300, 300, 300, 250
Проект В: -700, 300, 300, 300, 300, 300, 200
Первый проект имеет продолжительность 4 года, его NPV равно 138.0; второй проект должен осуществляться в течение 6 лет, его NPV составит 159.21. Таким образом, если проекты могут быть осуществлены лишь один раз, проект В имеет преимущество вследствие более высокого значения NPV. Однако, если проекты могут быть повторены неоднократно, более корректное сравнение может быть проведено путем повторения первого проекта три, а второго – два раза (12 – наименьшее общее кратное для числа лет осуществления проектов).
NPV проекта А, повторенного 3 раза составит
NPVА = -550+300/1.25+300/1.252+300/1.253+250/1.254 +
+ [-550+300/1.25+300/1.252+300/1.253+250/1.254]: 1.254 +
+ [-550+300/1.25+300/1.252+300/1.253+250/1.254]: 1.258 =
= 138 + 138/1.254 + 138/1.258 ≈ 217.68
NPV проекта В, повторенного 2 раза составит
NPVВ = - 700 +
+300/1.25+300/1.252+300/1.253+300/1.254+300/1.255+200/1.256 +
+[700+300/1.25+300/1.252+300/1.253+300/1.254+300/1.255+
+200/1.256]: 1.256 = 159.21 + 159.21/1.256 ≈ 200.95
Теперь уже сравнение оказывается в пользу проекта А.
Анализ инвестиционных проектов в условиях инфляции
Принятие инвестиционных решений в условиях существенного инфляционного изменения факторов, формирующих чистые денежные потоки, требует разработки специфических методов анализа. Наиболее корректным выглядит подход, основанный на прогнозе инфляционного изменения как притоков, так и оттоков денежных средств; при этом неявно делается предположение о том, что ожидаемая инфляция уже «учтена» в используемой ставке дисконтирования. Проблема здесь состоит, однако, в том, что прогнозирование инфляционного увеличения выручки и издержек на практике представляет собой достаточно сложную задачу в силу необходимости учета, наряду с прогнозным индексом роста потребительских цен, прогнозной динамики различных факторов (стоимости сырья и энергоносителей, валютных курсов, тарифов естественных монополий, мер тарифного и нетарифного регулирования импорта и экспорта и т.п.) В результате получается достаточно сложная многофакторная модель, затраты на построение которой отнюдь не обязательно оправдываются гарантированным качеством прогнозирования.
В качестве одного из приемов «смягчения» негативного влияния инфляции на качество анализа инвестиционного проекта часто рекомендуют перевод денежных потоков в «твердые» валюты, характеризующиеся незначительными темпами инфляционного обесценения. Однако с финансовой точки зрения такой прием имеет ряд существенных недостатков, делающих обоснованность полученных на его основе выводов сомнительной. Во-первых, темпы инфляционного обесценения одной и той же валюты в разных странах могут существенно различаться, соответственно, встает проблема оценки прогнозных темпов инфляции; во-вторых, в боьшинстве случаев платежи за реализованную продукцию осуществляются в национальной валюте, таким образом, пересчет в иностранную валюту влечет валютный риск, который также должен быть учтен при анализе инвестиционной привлекательности проекта.
Как следствие, в качестве компромисса между сложностью и реалистичностью инвестиционного анализа может быть предложена корректировка реальной[55] ставки дисконтирования на величину прогнозного среднегодового инфляционного изменения чистых денежных потоков. В качестве примера может быть рассмотрен следующий проект:
Пример. Фармацевтическая фирма рассматривает проект по организации торговли с лотков в нескольких крупных супермаркетах. Инвестиции в проект оцениваются в 1 млн. руб., чистые денежные потоки по годам: 500 тыс. руб.; 600 тыс. руб.; 800 тыс. руб. Срок экономической жизни проекта предусмотрен в 3 года. Стандартная ставка дисконтирования, принятая в компании для оценки эффективности проектов – 30%, однако по группе готовых форм, которые планируется предлагать в супермаркетах, прогнозное среднее подорожание составит 12% в год. Необходимо оценить инвестиционную привлекательность проекта без учета и с учетом инфляции.
Без учета инфляционного удорожания продукции NPV проекта составит (в тыс. руб.):
NPV = - 1000 + 500/ (1+0.3) + 600/ (1+0.3) 2 + 800/ (1+0.3) 3 = 103.778тыс. руб.
Таким образом, если использовать реальную ставку для дисконтирования номинальных денежных потоков, то проект выглядит приемлемым.
Для того, чтобы скорректировать ставку дисконтирования на ожидаемые темпы инфляции i необходимо использовать формулу Фишера:
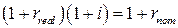
откуда

Номинальная ставка дисконтирования составит, таким образом, 45.6%. В этом случае
NPV = - 1000 + 500/ (1+0.456) + 600/ (1+0.456) 2 + 800/ (1+0.456) 3 = -114.383 тыс. руб.
Проект должен быть отвергнут.
Выбор инвестиционных проектов при лимитированном объеме финансовых ресурсов
Все предыдущие рассуждения неявно предполагали достаточность капитала для финансирования всех приемлемых инвестиционных проектов фирмы при неизменности его (капитала) стоимости. Если от этого допущения отказаться, то возникает проблема рационирования капитала. Всесторонний анализ этой проблемы выходит далеко за пределы базового курса управления финансами и выливается в дискуссию о возможности возникновения ситуации, в которой у фирмы не хватает средств для того, чтобы профинансировать все инвестиции, имеющие положительные NPV, то есть увеличивающие акционерную стоимость. В рамках принятых моделей и с точки зрения рационального управления финансами фирмы такая ситуация не должна возникать в принципе, так как привлекательные инвестиционные проекты должны адекватно финансироваться, хотя бы в силу того, что эффективный финансовый рынок должен «откликаться» на возможность получить возврат на инвестиции, превышающий стоимость привлекаемых средств. Однако финансовые рынки далеко не всегда в достаточной степени информационно эффективны; помимо этого, объемы инвестиционных ресурсов могут лимитироваться на дивизиональном уровне управления предприятиями, и в некоторых других ситуациях.
Наиболее простой вариант отбора проектов в условиях ограниченности инвестиционных ресурсов базируется на использовании критерия индекса доходности (см. выше). При этом предполагается, что стоимость капитала фирмы известна заранее и не зависит от принятия или непринятия тех или иных конкретных проектов, а сами проекты независимы. Отбор проектов тогда сводится к несложной процедуре, состоящей из двух этапов:
1. проекты с положительными NPV ранжируются по мере убывания их индексов доходности (PI);
2. проекты принимаются к реализации, начиная с первого в списке, пока суммарные начальные инвестиции в отобранные проекты не исчерпают установленный лимит капитальных вложений.
Следует при этом отметить, что описанная процедура не претендует на выработку оптимальной инвестиционной стратегии.
Инвестиционные решения, связанные с заменой оборудования
Практика использования метода расчета чистой приведенной стоимости проектов отнюдь не исчерпывается анализом рассмотренных выше ситуаций. Любое предприятие, занимающееся производственной либо торговой деятельностью рано или поздно сталкивается с необходимостью принятия решений, связанных с заменой оборудования. При этом в условиях крупных современных предприятий, характеризующихся несколькими уровнями управления, подобные решения часто делегируется с верхних уровней управления на более низкие, что требует формализации управленческих подходов. Последнее, в свою очередь, приводит к необходимости выработки политики в области замены оборудования.
Финансовую природу соответствующих управленческих решений рассмотрим на следующем примере.
Пример. Импортный станок стоимостью $16000, используемый при производстве медицинских инструментов имеет, по оценке его производителей, срок экономической жизни продолжительностью в 6 лет. По окончании этого периода вследствие износа деталей станок теряет требуемую точность, при этом капитальный ремонт не имеет экономического смысла. Ликвидационная стоимость станка после 6 лет эксплуатации равна нулю.
В силу высокотехнологичного характера производства и высокой конкуренции на рынке медицинских инструментов, денежные потоки даже в течение срока экономически обоснованной эксплуатации станка неравномерны (моральное старение оборудования снижает привлекательность изготавливаемой продукции в глазах потребителей).
Перед фирмой встает следующая проблема: эксплуатировать станок в течение всего срока его экономической жизни, или продать его до истечения нормативных 6 лет, заменив на более современную версию.
Чистые денежные потоки от реализации проекта (по годам) и динамика изменения рыночной стоимости представлены в таблице 4.1.
Таблица 4.1. Чистые денежные потоки от эксплуатации станка и его рыночная стоимость
| Год | ||||||
| Чистые денежные потоки ($ тыс.) | 8.0 | 7.5 | 7.0 | 6.5 | 6.0 | 5.5 |
| Рыночная стоимость станка* ($ тыс.) | 14.0 | 12.0 | 10.0 | 6.0 | 2.0 | 0.0 |
Если приемлемая ставка дисконтирования составляет 20%, то легко рассчитать NPV проектов, предусматривающих замену станка соответственно после одного, двух, трех, четырех, пяти и шести лет эксплуатации (все расчеты ведутся в тыс. долл.):
NPV1 = -16 + (8+14)/1.2 = 2.333
NPV2 = -16 + 8/1.2 + (7.5+12)/1.22 = 4.208
NPV3 = -16 + 8/1.2 + 7.5/1.22 + (7+10)/1.23 = 5.713
NPV4 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + (6.5+6)/1.24 = 5.954
NPV5 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + 6.5/1.24 + (6+2)/1.25 = 6.276
NPV6 = -16 + 8/1.2 + 7.5/1.22 + 7/1.23 + 6.5/1.24 + 6/1.25 + 5.5/1.26 = 7.314
Максимальная чистая приведенная стоимость эксплуатации станка в течение всего срока его экономической жизни не означает, однако, что именно этот вариант окажется в конечном счете оптимальным. В данном случае мы имеем дело с проектами различной продолжительности. Однако, в отличие от рассмотренных выше, эти проекты однозначно являются повторяющимся. Как следствие, каждый из проектов потребуется повторить столько раз, сколько это необходимо для достижения равного числа денежных потоков. Наименьшее общее кратное чисел 1, 2, 3, 4, 5 и 6 равно 60. Соответственно, решение задачи "вручную" методом цепного повтора потребует достаточно громоздких вычислений.
Date: 2016-05-23; view: 687; Нарушение авторских прав