
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вычисление и проверка однородности построчных дисперсий
|
|
1. Расчет средних значений удельного сопротивления резистивной пленки. Рассчитываются построчные средние значения удельных сопротивлений пленки
 ; (2.5)
; (2.5)
где  - сумма выходных параметров i -й строки, j -го столбца;
- сумма выходных параметров i -й строки, j -го столбца;
¯ q вых i - усредненное значение выходного параметра для параллельных опытов;
n - число дублирования опытов, т.е. n = 4.
2. Расчет построчных дисперсий удельного сопротивления резистивной пленки производится по формуле
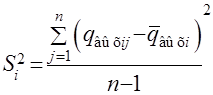 , (2.6)
, (2.6)
где Si2 - построчная дисперсия параллельных опытов;
q вых ij - выходной параметр i - строки и j - столбца.
3. Проверка однородности построчных дисперсий по критерию Фишера.
Исходя из полученных построчных дисперсий, определяем расчетное значение критерия Фишера по формуле

 , (2.7)
, (2.7)
где S2i max, S2i min- максимальная и минимальная построчные дисперсии,
Расчетное значение критерия F΄ Р сравнивается с табличным F΄ Т (табл.2.1).
Таблица 2.1
Значения критерия Фишера для 5%-ого уровня значимости от числа степеней свободы
| f1 | f2 | |||||
| 164.4 | 199.5 | 215.7 | 224.6 | 230.2 | 234.0 | |
| 18.5 | 19.2 | 19.2 | 19.3 | 19.3 | 19.3 | |
| 10.1 | 9.6 | 9.3 | 9.1 | 9.0 | 8.9 | |
| 7.7 | 6.9 | 6.6 | 6.4 | 6.3 | 6.2 | |
| 6.6 | 5.8 | 5.4 | 5.2 | 5.1 | 5.0 | |
| 6.0 | 5.1 | 4.8 | 4.5 | 4.4 | 4.3 |
Для 5%- ого уровня значимости и числа степеней свободы f΄1 =f΄2 = n – 1= 4 – 1 = 3, табличное значение F΄ Т = 9,3. Под числом степеней свободы в статистике понимают разность между числом опытов и количеством коэффициентов модели, вычисленных по результатам этих опытов независимо друг от друга.
При F' Р < F΄ Т построчные дисперсии считаются однородными. Если имеет место обратное соотношение, то это значит, что при проведении эксперимента были допущены грубые нарушения. В этом случае просматриваются значения удельных сопротивлений для строк, имеющих крайние значения дисперсий, вычеркиваются результаты опытов, значительно отличающихся от средних показаний. Вычисляются новые значения дисперсий и новое значение критерия F' Р , которое вновь сравнивается с табличным.
 4. Расчет коэффициентов полинома ( A0,…, Aj). Коэффициенты полинома рассчитываются по формулам
4. Расчет коэффициентов полинома ( A0,…, Aj). Коэффициенты полинома рассчитываются по формулам
 ; (2.8)
; (2.8)
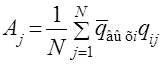 , (2.9)
, (2.9)
где N = 8 - число опытов ПФЭ;
qij - значение нормированного фактора, равное "+1" или "-1" из i -й строки j - го столбца.
После расчета коэффициентов составляется математическая модель процесса
 , (2.10)
, (2.10)
где  – число доминирующих факторов, равное 3.
– число доминирующих факторов, равное 3.
5.Расчет теоретических значений удельного сопротивления пленки  , полученных по математической модели для i -го режима напыления
, полученных по математической модели для i -го режима напыления
 (2.11)
(2.11)
6. Проверка адекватности модели. Для оценки адекватности полученной модели необходимо сравнить экспериментально полученные и рассчитанные по модели значения удельного сопротивления пленки. Проверка адекватности модели производится также по критерию Фишера, расчетное значение критерия определяется по формуле
 , (2.12)
, (2.12)
где  - значение удельного сопротивления пленки, вычисленное на основании полученной модели для i -то режима напыления; f1" - число степеней свободы при определении коэффициентов модели, равное N – l =8 - 3 =5; f2" - число степеней свободы при определении дисперсии эксперимента, равное N -1 = 4 – 1 = 3. Для 5%-го уровня значимости и f1" = 5, f2" = 3 табличное значение критерия равно F" табл = 5,4. Расчетное значение критерия сравнивается с табличным; если F" расч< F" табл, то с доверительной вероятностью 95% полученная модель считается адекватной исследуемому процессу, а исходная предпосылка о возможности линейной интерпретации процесса - правомерной.
- значение удельного сопротивления пленки, вычисленное на основании полученной модели для i -то режима напыления; f1" - число степеней свободы при определении коэффициентов модели, равное N – l =8 - 3 =5; f2" - число степеней свободы при определении дисперсии эксперимента, равное N -1 = 4 – 1 = 3. Для 5%-го уровня значимости и f1" = 5, f2" = 3 табличное значение критерия равно F" табл = 5,4. Расчетное значение критерия сравнивается с табличным; если F" расч< F" табл, то с доверительной вероятностью 95% полученная модель считается адекватной исследуемому процессу, а исходная предпосылка о возможности линейной интерпретации процесса - правомерной.
Date: 2016-05-18; view: 666; Нарушение авторских прав