Б) Равнопеременное движение

3.3.53. 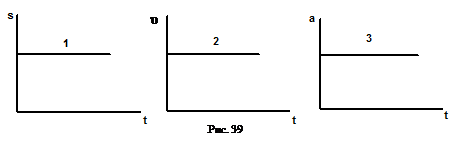Как движутся поезда 1, 2, 3, графики движения которых даны на рисунке 39?

3.3.54. Поезд движется равноускоренно и через 10 с после начала движения приобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равна 3 м/с?

3.3.55. Велосипедист движется под уклон с ускорением 0,3 м/с². Какую скорость приобретает велосипедист через 20 с, если его начальная скорость равна 4 м/с?

3.3.56. За какое время автомобиль, двигаясь с ускорением 0,4 м/с², увеличит свою скорость с 12 до 20 м/с?

3.3.57. От остановки одновременно отходят трамвай и троллейбус. Ускорение троллейбуса в два раза больше, чем трамвая. Сравните пути, пройденные троллейбусом и трамваем за одно и то же время, и приобретенные ими скорости.

3.3.58. Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см. Какой путь он пройдет за 3 с?

3.3.59. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с², пройдет 30 м?

3.3.60. Первый вагон трогающегося от остановки поезда проходит за 3 с мимо наблюдателя, находившегося до отправления поезда у начала этого вагона. За сколько времени пройдет мимо наблюдателя весь поезд, состоящий из 9 вагонов? Промежутками между вагонами пренебречь.

3.3.61. Материальная точка, движущаяся равноускоренно из состояния покоя, прошла за время t₁ путь s₁. За какое время t₂ (от начала движения) она пройдет путь s₂?

3.3.62. С каким ускорением движется снаряд в стволе пушки, если длина ствола равна 3 м и время движения в стволе равно 0,009 с? Какова скорость вылета снаряда?

3.3.63. Какую скорость приобретает ракета, движущаяся из состояния покоя с ускорением 60 м/с², на пути 750 м?

3.3.64. Bo сколько раз скорость пули в середине ствола ружья меньше, чем при вылете из ствола?

3.3.65. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.

3.3.66. Автомобиль, движущейся со скоростью 90 км/ч, потребовалось срочно остановить. При резком торможении ускорение равно 5 м/с². Через сколько секунд после нажатия тормозной педали автомобиль остановится?

3.3.67. Пуля при вылете из ствола автомата Калашникова имеет скорость 715 м/с. С каким ускорением и сколько времени движется в стволе пуля? Длина ствола 41,5 см.

3.3.68. При скорости υ₁ = 15 км/ч тормозной путь автомобиля равен s₁=1,5 м. Каким будет тормозной путь s₂ при скорости υ₂ = 90 км/ч? Ускорение в обоих случаях одно и то же.

3.3.69. Мотоциклист и велосипедист одновременно начинают движение из состояния покоя. Ускорение мотоциклиста в три раза больше, чем велосипедиста. Во сколько раз большую скорость разовьет мотоциклист: а) за одно и то же время; б) на одном и том же пути?

3.3.70. Имея начальную скорость 36 км/ч, троллейбус за 10 с прошел путь 120 м. С каким ускорением двигался троллейбус и какую скорость он приобрел в конце пути?

3.3.71. Уклон длиной 100 м лыжник прошел за 20 с, двигаясь с ускорением 0,3 м/с². Какова скорость лыжника в начале и в конце уклона?

3.3.72. Поезд, двигаясь под уклон, прошел за 20 с путь 340 м и развил скорость 19 м/с. С каким ускорением двигался поезд и какой была скорость в начале уклона?

3.3.73. Ускорение, которое может иметь во время движения троллейбус, не должно превышать 1,8 м/с². Определить, было ли нарушение правил, если водитель за 8 с увеличил скорость с 18 км/ч до 54 км/ч.

3.3.74. Автобус, имея скорость 6 м/с, продолжал двигаться равноускоренно с ускорением 1 м/с. На каком отрезке пути он увеличит скорость до 72 км/ч и за какое время?

3.3.75. Автобус, имея скорость 28,8 км/ч, начал двигаться равноускоренно и через 5,0 с приобрел скорость 57,6 км/ч. Определить путь, пройденный автобусом за это время.

3.3.76. Мотоциклист, двигаясь равноускоренно из состояния покоя, за пятую секунду проехал путь 18 м. Чему равно ускорение мотоцикла и какой путь он проехал за 5 с?

3.3.77. За пятую секунду равнозамедленного движения точка проходит 5 см и останавливается. Какой путь проходит точка за третью секунду этого движения?

3.3.78. Конькобежец, двигаясь равноускоренно, пробегает два одинаковых отрезка пути по 15 м соответственно в течение 2 с и 1 с. Определить ускорение и скорость его в начале первого отрезка пути.

3.3.79. Расстояние между двумя станциями поезд прошел со средней скоростью =72 км/ч за t=20 мин. Разгон и торможение вместе длились t₁ = 4 мин, а остальное время поезд двигался равномерно. Какой была скорость υ поезда при равномерном движении?

3.3.80. Зависимость скорости от времени при разгоне автомобиля задана формулой . Постройте график скорости и найти скорость в конце пятой секунды.

3.3.81. Скорость поезда за 20 с уменьшилась с 72 до 54 км/ч. Напишите формулу зависимости скорости от времени υ(t) и постройте график этой зависимости.

3.3.82. Пользуясь графиком скорости (см. рис. 40), найдите начальную скорость, скорости в начале четвертой и в конце шестой секунд. Вычислите ускорение и напишите уравнение .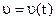

3.3.83. По заданным на рисунке 41 графикам напишите графикам запишите уравнения .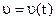

3.3.84. Зависимость скорости материальной точки от времени задана формулой υ=6t. Напишите уравнение s = s(t), если в начальный момент (t = 0) движущаяся точка находилась в начале координат (s₀=0). Вычислите путь, пройденный материальной точкой за 10 с.

3.3.85. Уравнение движения материальной точки, имеет вид s=25+0,4t². Напишите формулу зависимости υ(t)и постройте ее график. Покажите на графике штриховкой площадь, численно равную пути, пройденному точкой за 4 с, и вычислите этот путь.

3.3.86. Уравнение скорости движущегося тела υ = 5+4t (в СИ). а) Определите ускорение. б) Напишите соответствующее уравнение пути. в) Начертите график скорости. г) Начертите график зависимости координаты от времени при s₀ = 3 м.

3.3.87. Постройте графики зависимости скорости от времени, если: а) υ₀ = 5 см/с, а = 0; б) υ₀= 5 см/с, а = 1см/с²; в) υ₀= 0, а=1 см/с²; г) υ₀ = 10см/с, а = 2,5 см/с². Напишите соответствующие уравнения скорости.

3.3.88. Скорость поезда за 20 с уменьшилась с 72 км/ч до 54 км/ч. а) Определите ускорение. б) Напишите соответствующие уравнения зависимости скорости и пути от времени. в) Постройте график скорости и график пути в зависимости от времени.

3.3.89. Уравнение пути (в СИ) для движущейся точки имеет вид s = 3t-2t². а) Определите ускорение. б) Напишите соответствующее уравнение скорости движущейся точки. в) Постройте график скорости. г) Постройте график пути.

3.3.90. Изменение координаты со временем (в СИ) для движущейся точки имеет вид: Δs= 5t-2t². а) Определите ускорение. б) Напишите соответствующее уравнение скорости движущейся точки. в) Постройте график скорости. г) Постройте график пути.

3.3.91. Движение материальной точки задано следующим уравнением s = 5+10t+0,4t². Напишите зависимость υ(t); постройте график этой зависимости; определите вид движения.

3.3.92. Напишите уравнение s=s(t)для движений, графики скоростей которых даны на рисунке 41. Считайте, что в начальный момент (t = 0) тело находится в начале координат (s₀=0).

3.3.93. В таблице приведены значения мгновенной скорости автомобиля, относящиеся к моментам времени, отсчитываемым через 1 с. Постройте по этим данным график зависимости скорости от времени и используйте его для ответа на следующие вопросы:

а) является ли данное движение равноускоренным? Почему?

б) С какой скоростью двигался автомобиль в моменты времени 2,6 с; 4,8 с?

в) Чему равно ускорение?

3.3.94. Тело, двигаясь прямолинейно из состояния покоя с ускорением 5 м/с², достигло скорости 30 м/с, а затем, двигаясь равнозамедленно, остановилось через 10 с. Определите путь, пройденный телом за все время движения. Решите задачу графически.

3.3.95. Мальчик съехал на санках с горы длиной 40 м за 10 с, а затем проехал по горизонтальному участку еще 20 м до остановки. Найдите скорость в конце горы, ускорения на каждом из участков, общее время движения и среднюю скорость на всем пути. Начертите график скорости.

3.3.96. Велосипедист начал свое движение из состояния покоя и в течение первых 4 с двигался с ускорением 1 м/с²; затем в течение 0,1 мин он двигался равномерно и последние 20 м — равнозамедленно до остановки. Найдите среднюю скорость за все время движения. Постройте график υ(t).

3.3.97. Используя правило размерности, найдите ошибку в формуле: .

3.3.98. На поверхность Марса тело падает с высоты 100 м в течение примерно 7 с. С какой скоростью тело коснется поверхности Марса, падая с такой высоты?

1) 14,3 м/с. 2) 28,6 м/с.

3) 44,7 м/с. 4) 816 м/с.

3.3.99. Дано уравнение движения тела х = 5 + t + 1,5t². Чему равно ускорение? Запишите уравнение скорости для этого движения.

3.3.100. Движение тела описывается уравнением х = 12 + 6,2t – 0,75t². Определите скорость тела через 2 с после начала движения.

1) 0,4 м/с. 2) 3 м/с.

3) 3,2 м/с. 2) 3 м/с.

3.3.101. На рисунке 42 изображены графики зависимости ускорения от времени для разных движений. Какой из графиков соответствует равномерному движению?

1) График А. 2) График Б.

3) График В. 4) График Г.

3.3.102. Координаты пузырька воздуха, который всплывает в жидкости, были измерены в различные моменты времени и отмечены точками на каждом из четырех графиков (см. рис. 43). Погрешность измерения координаты равна 0,5 см, а времени — 0,5 с. Какой из графиков построен правильно с учетом всех результатов измерений и их погрешностей?

1) График А. 2) График Б. 3) График В. 4) График Г.

3.3.103. На рисунке 44 изображены графики зависимости модуля ускорения от времени движения. Какой из графиков соответствует равноускоренному прямолинейному движению?

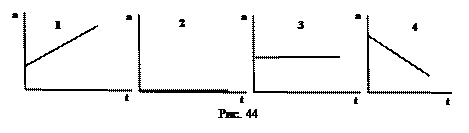
Динамика

Date: 2016-05-17; view: 2557; Нарушение авторских прав