Розв’язок кінетичного рівняння

Цей розв’язок розпадається на частини. Перша – розв’язок інтеграла зіткнень, друге – розв’язок векторного рівняння (1) відносно .

Введемо позначення

Тоді (1) матиме вигляд

τ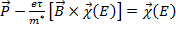

Помножимо скалярно на В і одержимо

τ

Помножимо векторно на В

τ

В результаті сумісного розв’язку останніх двох рівнянь знаходимо

Останній вираз для електронів (від’ємний заряд, другий член в чисельнику зі знаком +) всі константи потрібно взяти з індексом n. Для дірок (заряд позитивний) форма запису незмінна, але потрібно вставити індекси р.

Будемо вважати, що вектор магнітної індукції направлений вздовж осі z. В такому разі можна знайти компоненті вектора для електронів і дірок.

Знаючи компоненти , можна знайти густину електричного струму і потоку енергії, який переноситься вільними носіями заряду.

Густина струму електронів

,

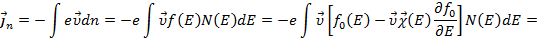
оскільки для рівноважних електронів

Аналогічно для густини потоку енергії , що переноситься електронами

Для слабких електричних полів виконується рівність для середніх значень

Тоді для і -ої компоненти (i = x, y, z) отримаємо

(2)

(3)

З розгляду отриманих рівнянь випливає, що в напрямі силових ліній індукції магнітного поля всі кінетичні ефекти не залежать від величини магнітного поля, у тому числі відсутній і магнітоопір.

Оскільки 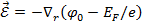, де φ₀ – електростатичний потенціал зовнішнього поля, отримаємо

(4)

(5)

Аналогічно з врахуванням теплопровідності ґратки отримаємо

(6)

(7)

Константи в останніх формулах (4)-(7) – це скорочений запис інтегралів, що входять до (2) і (3), підінтегральні вирази яких не містять електричного поля та температури.

Існують випадки, коли присутні електрони і дірки. В такому разі необхідно скласти компоненти струму для обох типів носіїв заряду.

Date: 2016-05-15; view: 369; Нарушение авторских прав