Модель Дебая твёрдого тела

Эффект Мёссбауэра связан с резонансным взаимодействием γ-кванта с ядром, при котором квантовое состояние решетки не меняется. Поэтому с помощью эффекта Мёссбауэра, казалось бы, нельзя получать информацию о движении атомов в решетке и о фононном спектре твердых тел. Однако имеется возможность изучения фононного спектра атомов в твердых телах посредством эффекта Мёссбауэра [38]. Она заключается в зависимости бесфононной части γ-лучей от колебательных свойств твердых тел.

Действительно,

где – средний квадрат амплитуды колебания атома в направлении испускания γ-кванта, усредненный по интервалу времени, равному времени жизни уровня; λ – длина волны γ-кванта.

Выражение (1) может быть записано в ином виде:

где

– энергия фотона. Для изотропного кристалла;

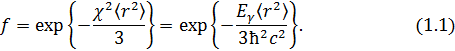
Зависимость безфононной части f от спектра колебания выражается, как видно из формулы (1), через Чтобы выяснить зависимость f от спектра колебания, рассмотрим, как связано со спектром колебания атомов в кристалле.

В теории физики твердого тела кристалл представляется как система 3N осцилляторов с частотой (N–число атомов). Полная средняя энергия, связанная с каждым осциллятором, равна

где – число фононов на уровне

Кинетическая энергия кристалла, приходящаяся на j- й осциллятор (в случае гармонического осциллятора), равна половине полной энергии, т.е.

С другой стороны,

откуда

где – смещение атомов от j-го осциллятора. Разделим обе части уравнения на и просуммируем по всем j:

Далее перейдем от суммирования к интегрированию, вводя плотность распределения частот ρ(ω):

или

Из выражений (2) и (3) следует зависимость от спектра колебания атомов в кристалле. Величины и f имеют интегральную зависимость от спектра колебаний. Поэтому, когда необходимо исследовать зависимость f от , измеряют f при различных температурах, т.е. снимают кривую зависимости и путем сравнения с теоретическими кривыми , вычисленными при различных , выбирают ту или иную модель, описывающую колебательные свойства кристалла.

В дебаевской модели твердого тела спектр частот колебания атомов имеет вид:

ρ(ω)=A ,

где А – нормировочных множитель, который находится из следующего условия:

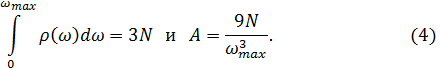
Подставляя выражение (4) в (2), получим:

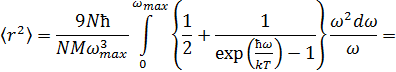
Введем температуру Дебая , равную

и проведем частичное интегрирование:

Обозначим После замены переменных находим, что

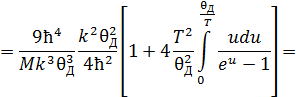
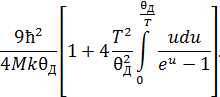
Полученный в последнем выражении интеграл берётся численно и рассматривается как функция двух переменных:

Подставим это выражение в формулу (1.1):

Поскольку в случае наноразмерных объектов температура Дебая может значительно отличатся от аналогичных величин для макроскопических материалов, для данной формулы не может быть использовано низко- и высокотемпературных приближений. Поэтому выражение (6) в случае наноразмерных объектов необходимо использовать в исходном виде как интегральную функцию.

Таким образом, изучая температурную зависимость f -фактора можно определить температуру Дебая, которая является важным динамическим параметром кристаллической решетки. Следующим шагом будет сравнение полученных таким образом данных с другими методами, которые описаны ниже.

Date: 2016-05-13; view: 570; Нарушение авторских прав