Закон Максвелла о распределении молекул по скоростям

Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.

В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией , называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные , то на каждый интервал скорости будет приходиться некоторое число молекул , скорости которых заключены в этом интервале.

Функция определяет относительное число молекул , скорости которых лежат в интервале от до , то есть

, откуда .

Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:

. (13)

Из (13) следует, что конкретное распределение зависит от рода газа (от массы молекулы ) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.

Выражение 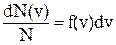представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу . Эта вероятность равна площади заштри-хованной полоски с основанием (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.

Площадь под кривой равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу , то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:

Наиболее вероятная , средняя арифметическая и

среднеквадратичная скорости молекул

Наиболее вероятная скорость соответствует максимуму функции распределения, ведь именно этой скоростью будет обладать наибольшее число молекул. Ее значение найдется из условия экстремума функции :

.

. (14)

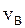Из формулы (14) видно, что при увеличении температуры максимум кривой распределения сместится вправо, так как при увеличении увеличивается , которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы 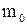будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6.

Выражение для средней скорости определяется по формуле

. (15)

Аналогично найдем выражение для среднеквадратичной скорости:

.

Произведя интегрирование, получим:

.

Из сравнения найденных скоростей вытекает:

.

Соотношения между скоростями:

При комнатной температуре средняя арифметическая скорость молекул кислорода будет равна:

.

Первое экспериментальное определение скоростей молекул было осуществлено Штерном в 1920 г: подтвердилась правильность оценки средней скорости молекул, вытекающей из распределения Максвелла; о характере распределения этот опыт дал лишь приближенные сведения. Более точно закон Максвелла был проверен в опыте Ламмерта (1929 г.).

Из функции распределения молекул по модулям скоростей можно получить функцию распределения молекул по кинетическим энергиям теплового движения:

.

Найдем среднюю кинетическую энергию молекулы идеального газа:

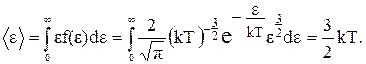
Date: 2016-05-15; view: 953; Нарушение авторских прав