
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Внутренняя энергия системы. Степени свободы молекул
|
|
Важной характеристикой термодинамической системы является ее внутренняя энергия. Как известно, энергия тела состоит из кинетической энергии движения тела со скоростью 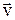 и потенциальной энергии тела во внешних силовых полях (гравитационном, магнитном и т. д.):
и потенциальной энергии тела во внешних силовых полях (гравитационном, магнитном и т. д.):
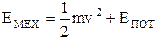 .
.
Согласно МКТ, все тела состоят из молекул, которые находятся в состоянии непрерывного, хаотического движения, то есть обладают кинетической энергией, а вследствие взаимодействия между собой обладают потенциальной энергией взаимодействия.
Внутренняя энергия – суммарная энергия хаотического (теплового) движения микрочастиц системы и энергия взаимодействия этих частиц.
Внутренняя энергия - однозначная функция термодинамического состояния системы (при переходе системы из одного состояния в другое изменение внутренней энергии определяется разностью значений внутренней энергии этих состояний и не зависит от пути перехода).
Как известно из механики, движение тел (или материальных точек) происходит в пространстве и во времени. Любое движение тела можно представить как комбинацию поступательного и вращательного движений. Положение тела в каждый момент времени характеризуется числом степеней свободы.
Число степеней свободы молекулы – число независимых переменных (координат), полностью определяющих положение системы в пространстве.
 Молекулу одноатомного газа (в виду ее малости) можно рассматривать как материальную точку, которой приписывают три степени свободы поступательного движения:
Молекулу одноатомного газа (в виду ее малости) можно рассматривать как материальную точку, которой приписывают три степени свободы поступательного движения:  (рис. 8).
(рис. 8).
Средняя кинетическая энергия поступательного движения одноатомной молекулы идеального газа равна:  .
.
Вращательные степени свободы в данном случае не учитываются, так как момент инерции данной молекулы относительно каждой из осей:  ,
,  ,
,  ,
,
 , следовательно
, следовательно  ,
, 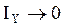 ,
,  , тогда кинетическая энергия вращения для каждой из осей:
, тогда кинетическая энергия вращения для каждой из осей:  .
.
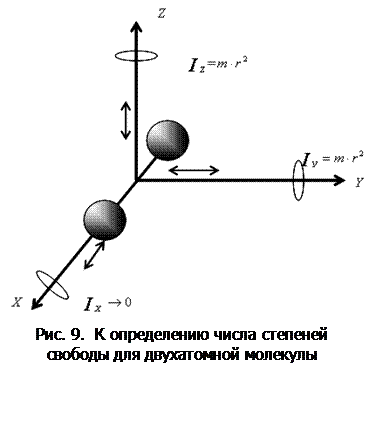 Молекула двухатомного газа рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 9). Кроме трех поступательных степеней свободы, у такой молекулы появляются две вращательные степени свободы относительно осей
Молекула двухатомного газа рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 9). Кроме трех поступательных степеней свободы, у такой молекулы появляются две вращательные степени свободы относительно осей  и
и  :
:
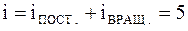 .
. Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (рис.10):
Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (рис.10):

 .
.
На самом деле, жесткой связи между атомами не существует. Атомы в молекуле могут сближаться и расходиться, то есть могут совершать колебания около положения равновесия. Энергия колебательного движения молекулы является суммой кинетической и потенциальной энергий, средние значения которых одинаковы. Таким образом, для реальных молекул необходимо учитывать также степени свободы колебательного движения.
В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная  , а на каждую колебательную степень свободы – в среднем энергия, равная
, а на каждую колебательную степень свободы – в среднем энергия, равная  . Средняя энергия молекулы равна:
. Средняя энергия молекулы равна:
 ,
,
где  .
.
Экспериментально установлено, что для молекулярного водорода при низкой температуре (≈50К) проявляются только поступательные степени свободы, при комнатной температуре (≈300К) добавляются вращательные, и лишь при высоких температурах (более 3000К) проявляются колебательные степени свободы.
Внутренняя энергия идеального газа складывается только из кинетических энергий всех молекул в данном объеме, так как потенциальной энергией взаимодействия молекул, согласно допущениям модели идеального газа (п. 1.3), можно пренебречь.
Для одного моля идеального газа:

Внутренняя энергия для произвольной массы идеального газа:

Date: 2016-05-15; view: 878; Нарушение авторских прав