Уравнение состояния идеального газа

Состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением , объемом 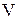и температурой . Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде задается выражением , где каждая переменная является функцией двух других.

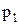Французский физик и инженер Б. Клапейрон объединил законы Бойля-Мариотта, Гей-Люссака и Шарля, и вывел уравнение состояния идеального газа. Пусть некоторая масса газа занимает объем , имеет давление и находится при температуре . Эта же масса газа в другом состоянии характеризуется параметрами 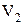, , 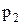(рис. 4).

Переход из состояния 1 в состояние 2 происходит в виде двух процессов: 1) изотермического (изотерма ), 2) изохорного (изохора ).

Согласно законам Бойля- Мариотта и Шарля:

, (3)

. (4)

Исключив из уравнений (3) - (4) 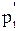, получим

.

Так как состояния 1 и 2 выбраны произвольно, то для данной массы газа величина остается постоянной, то есть

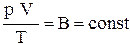. (5)

Выражение (5) является уравнением Клапейрона. Здесь – газовая постоянная, различная для разных газов.

Русский ученый Д.И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (5) к одному молю, используя молярный объем . Согласно закону Авогадро, при одинаковых 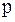и моли всех газов занимают одинаковый молярный объем , поэтому газовая постоянная будет одинаковой для всех газов. Эта постоянная обозначается и называется молярной газовой постоянной, она равна

.

Уравнению

(6)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, или уравнением Клапейрона- Менделеева.

От уравнения (6) для моля газа можно перейти куравнению Клапейрона – Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем , то при тех же условиях масса газа займет объем , где – молярная масса газа. Уравнение Клапейрона – Менделеева для массы газа

. (7)

Часто используют другую форму уравнения состояния идеального газа, вводя постоянную Больцмана:

.

Используя , запишем уравнение состояния идеального газа (7) в виде

Таким образом, из уравнения

(8)

следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа).

Date: 2016-05-15; view: 502; Нарушение авторских прав