Теорема Кели-Гамильтона и ее применение

Эта теорема имеет важное теоретическое значение и широко применяется в прикладных методах теории управления.

Теорема Кели - Гамильтона утверждает, что каждая матрица тождественно удовлетворяет своему характеристическому уравнению. Пусть характеристическое уравнение матрицы А имеет вид

. (4.17)

Тогда, по определению, справедливо тождество

, (4.18)

где О - нулевая матрица.

Соотношения (4.17) и (4.18) имеют простой смысл; любая квадратная матрица А, подставленная вместо собственных чисел в (4.17) «аннулирует» свое характеристическое уравнение , т. е. тождественно его удовлетворяет, аналогично тому, как каждый корень удовлетворяет уравнению (4.17). В этом смысле можно сказать, что каждая матрица является корнем своего характеристического уравнения.

В более полных руководствах приводятся раз­личные варианты доказательств этого принципиального результата. Следует отметить, что теорема Кели-Гамильтона распространяется на любые квадратные матрицы и не накладывает никаких ограничений на природу собственных чисел. Следовательно, теорема справедлива и для матриц с кратными собственными числами.

Можно показать, что полином, который «аннулируется» подстановкой матрицы А, не единственный, ибо если обладает этим свойством, то им обладает и всякий полином, делящийся на . Полином наименьшей степени, обладающий тем свойством, что матрица А является его «корнем», называется минимальным полиномом матрицы.

Можно установить, что характеристический полином всегда делится на минимальный полином. Более того, любой полином, обладающий «аннулирующим» свойством, т. е. удовлетворяющий требованию =О, делится на минимальный.

Кратное собственное число соответствует вырожденной матрице и ее характеристический полином является минимальным полиномом. Для любой матрицы ее минимальный многочлен единственен. Если все собственные числа матрицы А различны, то ее характеристический и минимальный многочлены совпадают.

Рассмотрим пример.

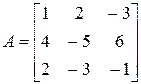
Характеристическое уравнение матрицы А имеет вид

Согласно теореме Кели - Гамильтона

Подставив в матричное уравнение квадрат и куб матрицы, получим

Отметим некоторые полезные применения тождества Кели - Гамильтона:

1) Вычисление целых положительных степеней матрицы.

Из равенства следуют равенства , и . Это дает возможность любую положительную степень матрицы А размерности линейно выразить через степеней и матрицу Е.

Пример 4.6 Матрица

имеет характеристическое уравнение .

В силу соотношения Кели - Гамильтона

,

откуда

,

,

2) Вычисление отрицательных степеней матрицы.

Если матрица А неособенная, то аналогично вышеизложенному можно получить отрицательные степени матрицы А и, в частности, построить обратную матрицу А^-1

Пример 4.7 Рассмотрим матрицу

В силу соотношения Кели - Гамильтона имеем:

,

,

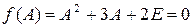Из последнего уравнения можно написать

,

откуда следует

Пример 4.8. Рассмотрим матрицу

Характеристическое уравнение ее имеет вид .

В силу тождества Кели - Гамильтона можно написать

Из этого соотношения легко получить отрицательные степени:

,

,

3) Любой матричный полином n-го порядка можно выра­зить через n-1 степеней матрицы А и единичную матрицу Е. Это означает, что любой полином или сходящийся степенной ряд от матрицы А может быть представлен в виде линейной комбинации , , ,..., . Например, если А - квадратная матрица размерности 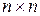, то

, (4.19)

где , - скалярные числа.

Заметим, что любые полиномы от одной и той же матрицы перестановочны между собой и коммутируют по отношению не только к операции сложения, но и умножения. Поэтому над матричными многочленами от одной и той же матрицы можно осуществлять алгебраические операции подобно тому, как это выполняется над скалярными многочленами.

Date: 2016-02-19; view: 479; Нарушение авторских прав