П1.2. Произведение множеств, проекции, диаграммы Эйлера-Венна

В результате прямого произведения множеств получится множество различных кортежей длиной равной n (упорядоченных n-нок), вида:

Проекция такого множества представляет собой множество проекций кортежей данного множества. Пусть V –множество кортежей v, тогда множество проекций кортежей будет следующего вида Рассмотрим практические задачи на прямое произведение множеств. Пусть заданы следующие множества , жјне . Необходимо выполнить операцию прямого произведения множеств . Для этого необходимо сперва перемножить множества А и В, В результате получится множество кортежей длиной равной двум:

.

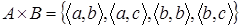Далее полученный результат умножим на множество С, в результате получится множество кортежей длиной равной трем:

.

После этого можно выполнить операцию прямого произведения результирующего множества на множество D, получим множество кортежей длиной равной четырем:

.

Далее определим различные проекции полученного множества кортежей:

,

,

,

.

По заданной диаграмме Эйлера-Венна необходимо определить выражение описывающее заштрихованную область (рисунок 1.1). Для этого разобъем исходную область на две части. Первая часть представляет собой множество находящееся внутри множеств А и В и снаружи множества С, поэтому результирующее множество можно описать в виде следующего выражения:

.

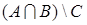Далее опишем вторую часть являющуюся внутренней частью множеств А и С и наружней часть множества В, которая описывается выражением вида:

.

Далее объединим полученные множества и опишем заштрихованную область в виде:

.

Пусть заданы следующие множества , и .

Докажем на примере этих множеств правильность законов теории множеств. Сперва рассмотрим сочетательный закон:

.

, ,

.

,

.

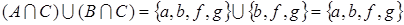Последнее выражение доказывает правильность сочетательного закона.

Теперь докажем законы де Моргана используя вышеприведенные множества. Первый закон имеет следующий вид:

Вычислим левую часть данного выражения, для этого необходимо в начале определить универсальное множество І:

отсюда

.

Вычислим правую часть выражения:

,

Полученные результаты совпали, что говорит о правильности первого закона де Моргана.

Докажем следующий закон де Моргана:

.

Вычислим правую часть этого выражения:

.

Вычислим левую часть исходного выражения:

.

Последнее выражение подтверждает правильность закона де Моргана.

Date: 2016-02-19; view: 675; Нарушение авторских прав