Уточнення коренів

До найбільш поширених методів уточнення коренів алгебричних і трансцендентних рівнянь відносять методи:

– половинного ділення (інші назви: бісекції, дихотомії);

– хорд (помилкового положення);

– дотичних (Ньютона);

2.4.1 Метод половинного ділення

Суть методу, в тому, що відрізок ізоляції кореня [а, b] ділять навпіл точкою х₁ = 0,5(а+b) і обчислюють f(x₁). Якщо f(x₁) = 0, то х₁ є точне значення кореня. Якщо f(x₁) ¹ 0, але (b-a) £ 2ε (ε – задана точність визначення кореня), то х₁ – є наближене значення кореня що знайдено із заданою точністю. Якщо f(x₁) ¹ 0 і

(b-a) > 2ε, тоді розглядають той з двох відрізків [a, x₁] і [x₁, b], на кінцях якого функція f(x₁) набуває значень протилежних знаків (рис. 2.1). Цей відрізок знов ділять навпіл точкою х₂ (друге наближення кореня) і так само визначають, чи не перевищує абсолютна похибка наближення кореня х₂ величини ε. Очевидно, що знаходження чергового наближення кореня після n ітерацій здійснюється за виразом

x_n+1 = 0,5(a_n + b_n). (2.5)

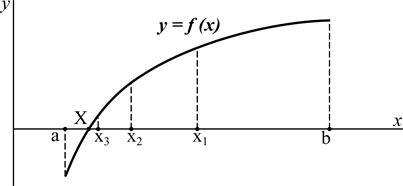
Рисунок 2.1 – Графічне зображення суті методу половинного ділення

Алгоритм методу половинного ділення можна зобразити таким чином:

Завдання a, b, ε;

R = f(a);

► x = 0,5(a + b);

f(x);

якщо то х – корінь;

да, то ►

інакше R·f(x) < 0?

ні, то 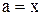, R = f(x) ►.

2.4.2 Метод хорд

В цьому методі відрізок С ділять не навпіл, а у відношенні f(a) / f(b). Суть методу полягає в тому, що за наближення до кореня приймаються значення x₁, x₂, x₃, …, x_n точок перетину хорди з віссю абсцис (рис. 2.2).

Рисунок 2.2 – Графічне зображення ідеї методу хорд

Наступне наближення кореня визначається за формулою

(2.6)

де с – так звана нерухома точка, за яку приймається той з кінців відрізка [а, b], для котрого знак функції збігається зі знаком другої похідної (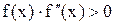). На рис. 2.2 с = а. Другий кінець відрізка [а, b] приймається за початкове наближення х₀, що використовується формулою (2.6).

Ітераційний процес закінчується при виконанні умови

,

де – найменше значення модуля першої похідної на відрізку [а, b].

Для використання методу хорд необхідно для інтервалу [a, b] обчислити

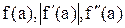і . За допомогою одержаних значень визначити величини m, c, x₀ таким чином: ; якщо f(a) і мають однаковий знак, то с = а і х₀ = b (відповідно, якщо однаковий знак мають f(b) і , то с = b і х₀ = а).

Далі алгоритм методу хорд виглядає так:

Завдання ε, m, c, x₀;

f(c);

R = f(x₀);

► x = ;

f(x);

якщо 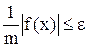, то х – корінь;

інакше: R = f(x), x₀ = x ►.

2.4.3 Метод дотичних

Метод полягає в побудові ітераційної послідовності

, (2.7)

що збігається до кореня рівняння f(x) = 0.

Достатні умови збіжності метода: послідовність (2.7) збігається до дійсного значення кореня рівняння f(x) = 0, якщо початкове наближення кореня (х₀) належить інтервалу [а, b], на котрому 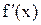і зберігають свій знак і задовольняється умова .

За х₀ приймають той з кінців відрізка [а, b], для якого (в методі хорд це нерухома точка).Метод допускає просту геометричну інтерпретацію, а саме: якщо через точку з координатами провести дотичну, то абсциса точки перетину цієї дотичної з віссю х і є чергове наближення кореня рівняння f(x) = 0 (рис. 2.3).

Ітерації продовжуються до виконання умови

,

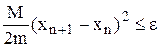Де М – найбільше значення модуля другої похідної на відрізку [а, b],

.

Рисунок 2.3 – Графічне подавання ідеї методу дотичних

Для використання методу дотичних необхідно для інтервалу [a, b] обчислити 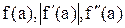і . За допомогою одержаних значень визначити величини m, М, x₀ таким чином: ; , якщо f(a) і мають однаковий знак, то х₀ = а.

Далі алгоритм методу дотичних може виглядати так:

Завдання ε, m, М, x₀;

► х = х₀;

f(x);

;

якщо , то х – корінь;

інакше: x₀ = x ►.

Метод дотичних має високу швидкість збіжності, однак недоліком його є необхідність обчислення похідної 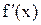на кожній ітерації. Якщо 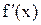мало змінюється на відрізку [а, b], то можна значно зменшити обсяг обчислень, якщо скористуватися модифікованим методом Ньютона з використанням формули

.

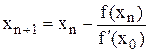2.4.4 Комбінований метод хорд і дотичних

Методи хорд і дотичних дають наближення кореня з різних боків. Тому їх часто поєднують і уточнення кореня відбувається скоріше.

На кожній ітерації використовується спочатку формула (2.7), потім – формула (2.6), в якій за с приймають значення x, що розраховано на даному кроці за формулою(2.7). Процес закінчується, коли Остаточне значення кореня визначається формулою

, (2.8)

де і – наближення кореня, які розраховані відповідно за формулами (2.6) і (2.7).

2.4.5 Метод ітерацій

Для знаходження кореня методом ітерацій (простих) рівняння f(x) = 0 приводять до вигляду так, щоб виконувалось співвідношення 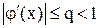, яке є достатньою умовою збіжності ітераційного процесу.

На інтервалі [а, b] обирають початкове наближення х₀ (бажано в середині інтервалу, щоб похибка заокруглення не вивела за межі [а, b], де виконуються умови збіжності); наступні наближення визначаються за формулою

(2.9)

доти, поки не буде виконано умову

(2.10)

(можна прийняти ).

З геометричної точки зору коренем рівняння є абсциса точки перетину кривої і прямої

Характер зміни в процесі обчислень за формулою (2.9), а також вид умови закінчення ітерацій залежать від знака і абсолютної величини на інтервалі [а, b].

– Якщо , то послідовні наближення сходяться до кореня монотонно. При цьому, якщо q £ 0,5 за умову закінчення ітерацій можна прийняти

. (2.11)

– Якщо , то послідовні наближення коливаються навколо дійсного значення кореня і при цьому також можна користуватися умовою (2.11). Таким чином, умову (2.10) необхідно використовувати тільки в тих випадках, коли і .

Не завжди легко обрати функцію , що задовольняє умові збіжності.

Розглянемо один з алгоритмів переходу від рівняння до рівняння Помножимо ліву і праву частини рівняння на довільну константу h і додамо до обох частин невідоме х

при цьому корені вихідного рівняння не зміняться.

Позначимо і одержимо

Очевидно, що при будь-яких рівняння і рівносильні. Константу бажано обрати такою, щоб , тоді буде забезпечена збіжність ітераційного процесу.

Похідна . Найбільша швидкість збіжності має місце при , тоді і ітераційна формула (2.9) переходить у формулу Ньютона (метода дотичних)

.

Date: 2016-02-19; view: 461; Нарушение авторских прав