
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Условие постоянства функции на промежутке
|
|
Т: пусть ф-ция y=¦(x) определена на промежутке X=[a, b] и внутри него имеет конечную производную ¦ ¢ (x), если в каждой точке этого промежутка ¦ ¢ (x)=0, то f(x)ºc - const.
Док-тво:
|
Это условие достаточно и необходимо (условие: ¦ ¢ (x)=0), т.к. если f(x) - const, то f ´ (c)=0.
Следствие: рассмотрим 2 ф-ии f(x) и g(x), определенные в некотором промежутке Х и имеющие внутри него конечные производные f ´ (x) и g ´ (x). Если для всех хÎХ, f ´ (x)=g ´ (x), то на всем промежутке Х эти функции отличаются др. от др. лишь на постоянную, т.е. f(x)=g(x)+с, c-const.
Обратная: если f ´ (x)=0 и ф-ция дифференцируемая, то по Т. Лагранжа Dy=f ´ (x)*Dx=0, т.е. приращение ф-ции =0 при " Dx => Dy=0 при " Dx => ф-ция м.б. только const.
Возрастание и убывание ф-ии на пром-тке (монотонность):
Возрастание: y=f(x); x1<x2;f(x1)<f(x2); Ккас>0; f ´ (x0)= Ккас>0.
Убывание: y=f(x); x1<x2;f(x1)>f(x2); Ккас<0; f ´ (x0)= Ккас<0.
Опр: y=f(x) наз-ся ↑- щей { ↓ -щей} на [a, b], если "x1, x2 Î [a, b], таких, что х1 < x2 соответствующие значения ф-ции удовлетворяют неравенству f(x1)<f(x2) {f(x1)>f(x2)}.
Необход-мое условие: T1 и Т1 ´: если ф-ия y=f(x), имеющая производную на [a, b], возрастает {убывает} на этом отрезке, то ее произв-ная на [a, b] f ´ (x)³0 { f ´ (x)£0}
Док-тво: y=f(x)- возрастает. Док-жем, что f ´ (x)³0.

(a) при ∆x>0; x<x+∆x => f(x+∆x)-f(x)>0 б) при ∆x<0; x>x+∆x => f(x+∆x)-f(x)<0 ) =>  , т.е.
, т.е.
" ∆x:  в силу соотв-вий Т о пределах. Т - док-на.
в силу соотв-вий Т о пределах. Т - док-на.
Аналогично док-тся Т1 ´.
Достаточное условие: Т2 и Т2 ´: если ф-ия y=f(x) непрерывна [a, b] и дифференцируема в промежутке (a, b), причем f ´ (x)>0 {f ´ (x)<0} для всех хÎ(a, b), то эта ф-я возрастает {убывает} на [a, b].
y=f(x) - определена и возрастает на [a, b], диф-маркетинг в (a, b); f ´ (x)>0. Док-ем, что f(x) - возрастает на [a, b].
x1, x2Î[a, b]; x1<x2; док-ем, что f(x1)<f(x2); f(x1)-f(x2)=f ´ (c)*(x1-x2), где с - м/у х1 и х2, т.е. x1<c<x2 => cÎ[a, b], т.е. f ´ (c)>0 (по усл). Так как х1<x2, то х1-x2<0 => f ´ (c)*(x1-x2)<0; f(x1)-f(x2)<0, т.е. f(x1)<f(x2) => y=f(x) - возрастает.
Экстремум:f(x) на [a,b] имеет в x0 Î [a,b] max {min}, если $ такая окрестность т. х0 (х0-d, х0+d), что для всех х из этой окрестности (кроме х0) справ нер – во f(x)<f(x0) {f(x)>f(x0)}. Необх-мое усл-ие экстремума (Т Ферма) Пусть f(x) опред-на на нек-ром промеж-ке, и во внутр-ей т-ке х0 этого пром-ка имеет наиб-шее и наим-шее значение. Тогда если в т х0 $ конечная произв-ная то она = 0, т. е. f/(х0) = 0, то точка х0 - точка экстремума.
Дано: y=f(x); xÎD(f); f ´ (x) $ для хÎD(f); x0-точка max (min).
Док-ем, что f ´ (x)=0.
Т.к. х0 - точка экстемума, то $ некоторая d - окрестность в точке х0: (х0-d, х0+d)ÎD(f), относительно, которой f(x0) является наибольшим (наименьшим) значением ф-ции, т.е. на интервале (х0-d, х0+d) для ф-ции y=f(x) выполняется условие теоремы Ферма => f ´ (x)=0.
Но это необх-мое, но не дост-ное усл –е, м. оказаться, что в т-ке х0 произв = 0, но экстремума в ней нет. Примером такой f=x3 в т х0= 0.
Достаточное условие экстремума: пусть ф-я y=f(x) непрерывна в некотором интервале, содержащем критическую точку х1 и дифф-ма во всех точках этого интервала (кроме б. может самой точки х1), если при переходе слева направо ч/з точку х1 производная меняет знак с "+" на "-", то при х=х1 ф-я имеет максимум. Если при переходе слева направо ч/з т. х1, производная меняет знак с "-" на "+", то ф-я имеет в этой точке минимум.
Док-тво: пусть х1 - критическая точка, f ´ (x)>0 при x<x1 и f ´ (x)<0 при x>x1. Докажем, что х1- точка max, другими словами f(x)<f(x1) для некоторой окрестности точки х1.
х1-d,х,c,х1,c,x,х1+d
пусть x<x1, тогда на [x, x1] ф-я y=f(x) удовлетворяет теореме Лагранжа, f(x1)-f(x)= f ´ (c)*(x1-x)>0 => f(x)<f(x1).
пусть x>x1, тогда на [x1, x] ф-я y=f(x) удовлетворяет теореме Лагранжа, f(x)-f(x1)= f ´ (c)*(x-x1)<0 => f(x)<f(x1). Т.е. для "хÎ(х1-d, х1+d); f(x)<f(x1) => точка х1 - точка max.
Т: достаточное условие $ экстремума в терминах 2-ой производной: пусть в точке х1 из D(f), f ´ (x)=0 и f ´´ (x) $ и непрерывна в некоторой окрестности точки х1. Тогда при х=х1 ф-я имеет максимум, если f ´´ (x)<0 и минимум, если f ´´ (x)>0. Алгоритм нахождения наибольшего и наименьшего значения ф-и на [a,b]: 1. найти критические точки.(f ´ (x)=0) 2. Из найденных критических точек выбрать те которые Î[a, b]. 3. Вычисляются значения ф-ии в критических точках, Î[a, b] и на концах отрезка. 4. Из полученных значений выбир-тся наибольшее и принимается за набольшее значение ф-ии и наименьшее, которое принимается за наименьшее значение ф-ии на этом отрезке.
Т. Ферма: пусть ф-ия y=f(x) определена в некотором промежутке X=[a,b] и во внутренней точке с, (т.е. a<c<b) этого промежутка принимает наибольшее (наименьшее) значение, если в этой точке $ конечная производная f ´ (c), то необходимо f ´ (с)=0.
Точки в которых произв = 0, не $,¥ называются стационарными или подозр-ми на экстремум. Пусть т х0 – одна из подозр точек, предположим в некоторой окрестн-ти (х0-d, х0+d) за исключ х0 $ конечн произв имеющая н (х0-d, х0) и (х0, х0+d) постоян знаки. В зависим от распред знаков слева и справа от х0 возм случаи: 1) f/(x)>0 при х < х0 и f/(x)<0 при х > х0, т. е. в т х0 – max; 2) f/(x)<0 при х < х0 и f/(x)>0 при х > х0, т. е. в т х0 – min;3) f/(x)>0 при х < х0 и f/(x)>0 при х > х0 или f/(x)<0 при х < х0 и f/(x)<0 при х > х0 в т х0 ни max, ни min. Итак, если ф – ция меняет знак при переходе ч – з т х0, то в этой точке ф – ция имеет экстремум. Это дост усл – е экстремума. Пример: у = 1/3х3-5/2х2+6х, у/ = х2 - 5х + 6, у/=0, х2 - 5х + 6=0, х1= 2, х2 = 3 – эти точки подозр на экстр, других точек подозр на экстр нет. Имеем, у/<0 при 2<x<3 и у/>0 при х>3, т. е. х2 – min. Выпукл и вогн Кривая в т М вогнута вниз (вверх), если в некоторой ее окрестности она лежит ниже (выше) касат-ной. М – т перегиба, если кривая переходит в М с одной стороны касат на другую.
Кривая на [a,b] называется выпуклой вверх {выпуклой вниз} если все точки кривой лежат ниже {выше} любой ее касательной на этом отрезке.
Т и Т ´: если во всех точках отрезка [a,b] вторая производная ф-и f(x) отрицательна {положительна}, т.е. f ´´ (x)<0 { f ´´ (x)>0}, то кривая y=f(x) на этом промежутке выпукла вверх {выпукла вниз}.
Док-тво: y=f(x); xÎ[a,b]; f ´´ (x)<0; xÎ(a,b). Докажем, что y=f(x) выпукла вверх.
x0Î[a,b].  - ординаты точек касательной.
- ординаты точек касательной. 
 -y0= f ´ (x0)*(x-x0) или
-y0= f ´ (x0)*(x-x0) или  =f(x0)+f ´ (x0)*(x-x0).
=f(x0)+f ´ (x0)*(x-x0).
1. пусть x<x0. Оценим разность.  - y= f(x0)+f ´ (x0)*(x-x0)-f(x)=(f(x0)-f(x))+f ´ (x0)*(x-x0)= f ´ (c1)*(x0-x)+ f ´ (x0)*(x-x0)= f ´ (c1)*(x0-x)-f ´ (x0)*(x0-x)=[ f ´ (c1)-f ´ (x0)]*(x0-x)= f ´´ (c2)*(c1-x0)*(x0-x)>0, т.е.
- y= f(x0)+f ´ (x0)*(x-x0)-f(x)=(f(x0)-f(x))+f ´ (x0)*(x-x0)= f ´ (c1)*(x0-x)+ f ´ (x0)*(x-x0)= f ´ (c1)*(x0-x)-f ´ (x0)*(x0-x)=[ f ´ (c1)-f ´ (x0)]*(x0-x)= f ´´ (c2)*(c1-x0)*(x0-x)>0, т.е.  =>
=>  >y для x<x0.
>y для x<x0.
2. Пусть x>x0.  - y= f(x0)+f ´ (x0)*(x-x0)-f(x)=(f(x0)-f(x))+f ´ (x0)*(x-x0)= [ f ´ (c1)-f ´ (x0)]*(x0-x)= f ´´ (c2)*(c1-x0)*(x0-x)>0, т.е.
- y= f(x0)+f ´ (x0)*(x-x0)-f(x)=(f(x0)-f(x))+f ´ (x0)*(x-x0)= [ f ´ (c1)-f ´ (x0)]*(x0-x)= f ´´ (c2)*(c1-x0)*(x0-x)>0, т.е.  =>
=>  >y для x<x0
>y для x<x0
y=f(x) выпукла вверх на [a,b].
Т. Лагранжа: пусть 1. Ф-я y=f(x) определена и непрерывна в [a,b]. 2. $ конечная производная f ´ (х) по крайней мере в открытом промежутке (a,b), тогда м/у a и b найдется такая точка с, a<c<b, что выполняется равенство:
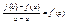
Опр: точка, отделяющая выпуклую вверх часть непрерывной кривой от выпуклой вниз называется точкой перегиба кривой.
Опр: точки, в которых вторая производная =0, или не $ (при существовании самой функции) называются критическими точками второго рода.
Т (достаточное условие существования точки перегиба): пусть кривая определяется уравнением y=f(x), если f ´´ (х0)=0 или f ´´ (х0) не $ и при переходе ч/з эту точку х0, производная f ´´ меняет знак, то точка х0 - точка перегиба.
Признаки: выпукл кривой f//<0, вогн-ть кривой f//>0, необх-мый признак перегиба f//=0.
Асимптоты. Прямая х = а явл – ся вертикальной асимптотой графика у = f(x), если хотя бы одно из предельных зн-йlim f(x) = ±¥при х®а+0 или х®а – 0.
Опр: прямая линия называется асимптотой для кривой y=f(x), если расстояние от т. М Î кривой до прямой ®0 при движении точки М вдоль какой - нибудь части кривой в ¥.
Вертикальная асимптота: х=а - вертикальная асимптота к графику ф-ии y=f(x), если

если  , то х=а -вертик-я асимптота, если В(а)¹0, А(а)=0.
, то х=а -вертик-я асимптота, если В(а)¹0, А(а)=0.
Наклонные асимптоты: y=f(x); y=kx+b;

Опр: прямая y=k1x+b1 называется левосторонней наклонной асимптотой (или асимптотой при х®-¥) к графику ф-ции y=f(x), если

Опр: прямая y=k2x+b2 называется правосторонней наклонной асимптотой (или асимптотой при х®+¥) к графику ф-ции y=f(x), если
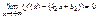
Если k=k1=k2; b=b1=b2, то прямая y=kx+b называется наклонной асимптотой при х®¥.
Для того, чтобы прямая была левосторонней (правосторонней) наклонной асимптотой для графика ф-ии y=f(x) необходимо и достаточно, чтобы существовали конечные пределы:


Т. Лагранжа. y=f(x) определена и непр. на [a,b], и на [a,b] $ конечная f ¢(x), тогда внутри найдется какая т. с, что
 .
.
Пр-ло Лопиталя: пусть: ф-ции f(x) и g(x): 1. Б/М (или Б/Б) при х®а; 2. Дифференцируема в окрестности точки х=а, т.е. (а-d, а+d); 3. g ´ (x)¹0 в указанной окрестности за исключением быть может х=а; 4. $ конечный или бесконечный предел
 , тогда $ и предел
, тогда $ и предел 
На основе этой теоремы фор-ся правило Лопиталя для раскрытия неопределенности:
Правило: предел отношения ф-ций = пределу отношения их производных.
Date: 2016-02-19; view: 817; Нарушение авторских прав