В тетрадке

Вопрос 17. Все свойства определителей (с док-вами, где были).

1) | A^T | = | A |, т.е. определитель не меняется, если заменить его строки столбцами и обратно: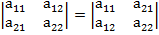

2) Перестановка двух строк(столбцов)определителя меняет его знак на противоположный.: = -

3) Определитель, у которого элементы одной строки(столбца) пропорциональны (или равны) соответствующим элементам другой строки(столбца), равен 0.

Например: =0

4) Если все элементы какой-нибудь строки(столбца) равны 0, то определитель равен 0

5) При умножении определителя на какое-либо число, то на это число умножаются элементы какой-нибудь одной строки(столбца). Либо из элементов какой-либо строки можно вынести общий множитель

6) Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали

7) Если к строке (столбцу) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число, то определитель не изменит своей величины

8) Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например

Вопрос 18. Обратная матрица. Теорема о существовании и единственности обратной матрицы. Способ вычисления обратной матрицы.

Определение: Матрица 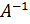называется обратной квадратной матрице А, есть А=А 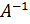=I, где I-единичная матрица

Определение: Квадратная матрица называется неособенной, если |А|≠0

Теорема: Для того, чтобы у матрицы А существовала обратная, необходимо и достаточно, чтобы матрица А была неособенной. Если 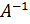существует, то она единственна.

Способы вычисления обратной матрицы:

Первый способ (через союзную матрицу): 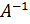= A^*, где A^*- союзная матрица, составленная из алгебраического дополнения и транспонирования.

Второй способ (через единичную): Нужно построить матрицу (А|E), где E – единична матрица того же размера, что и матрица A. Выполняя элементарные преобразования со строками матрицы (А|E), нужно привести эту матрицу к виду (B|E), тогда B=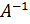

Вопрос 19. Определение ранга матрицы. Базисный минор. Вычисление ранга матрицы с помощью элементарных преобразований.

Определение: Рангом r(A) матрицы A называется наибольший из порядков ее не равных 0 миноров. Ранг нулевой матрицы принимается равным 0.

Ранг прямоугольной матрицы удовлетворяет неравенству 0≤r(A)≤min{m;n}. Если матрица квадратная 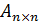, то 0≤r(A)≤ n. Если матрица 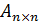- неособенная, |A|≠0, то ее ранг равен n

Определение: Не равный 0 минор, порядок которого равен рангу матрицы, называется базисным. Матрица может иметь несколько базисных миноров.

Чтобы вычислить ранг произвольной матрицы и найти ее базисный минор, удобно привести ее с помощью элементарных преобразований к трапецеидальному виду. Если в результате преобразований возникла матрицы, содержащая несколько пропорциональных(равных) строк, то надо оставить одну из них без изменений, обратив остальные строки в нулевые

Элементарными преобразованиями матрицы называются следующие:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответсвующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Вопрос 20. Системы линейных уравнений и ее решение. Теорема Кронекера-Капелли (док-во)

· Система m линейных уравнения с n неизвестными называется выражение вида:

где x_1,x₂,…x_m – неизвестные, a_ij – коэффициенты при неизвестных, b_i – свободные члены.

· Систему можно записать в матричной форме: Ax=B, где

, ,

А – матрица системы, X - столбец неизвестных, B – столбец свободных членов.

· Система, записанная в векторной форме имеет вид:

, где A_j – столбец коэффициентов при неизвестной x_j

Cистема может быть: несовместной (нет решений) и совсестной (хотя бы одно решение), совместная(определенная) – если имеет единственное решение, совместная(неопределенная) – если имеет бесконечное множество решений

Решение систем:

· Ax=B; x= B

· Решение системы методом Крамера (если ∆ ≠ 0): сначала находим определитель ∆, затем эл-ты определителя заменяем столбцом свободных членов, считаем новый определитель ∆n, таким образом

· Если ( ∆=0) нужно использовать метод Гаусса: метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

Теорема Кронекера-Капелли - критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство: Необходимость Пусть система совместна. Тогда существуют числа x₁,…..x_n, Є R такие, что b=x₁a₁+….+x_na_n. Следовательно, столбец b является линейной комбинацией столбцов a₁,…,a_n матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что rang(A)=rang(B).

Достаточноть Пусть rang(A)=rang(B)=r. Возьмем в матрице A какой-нибудь базисный минор. Так как rang(B)=r, то он же и будет базисным минором и матрицы B. Тогда, согласно теореме о базисном миноре, последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Вопос 21. Теорема Крамера.

Теорема: Если главный определитель системы линейных уравнений с квадратной матрицей отличен от 0(∆ ≠ 0), то система имеет единственное решение, которое можно найти по формулам

, где n=1,2,...n.

Доказательство:

Предположим, что |A|≠0. Тогда существует обратная матрица. Умножив слева обе части равенства на , получим

Таким образом, система уравнений имеет единственное решение и оно в матричной форме может быть записано в виде (1)

обратная матрица находится по формуле 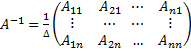, где Aij -алгебраические дополнения. Тогда из (1) следует, что

X= =

разложение определителя по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя по второму столбцу дает второй элемент матрицы-столбца и т.д

Поэтому x= , откуда и следует утверждение теоремы.

Вопрс 22. Теорема: необходимое и достаточное условие определенности системы уравнений.

Кронекера–Капелли: Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы: rang(A)=rang()

Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.

Теорема 1 Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой

Теорема 2 Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.

Тогда:

1) при r ≠ система несовместна (нет решений)

2) при r = система совместна, причём, если r = = n, система определённая; если же r = < n, система неопределённая.

! Для того, чтобы система была определенной необходимо и достаточно, чтобы ранг совместной системы был равен числу неизвестных r = = n.

Впорос 23. Теорема: необходимое и достаточное условие неопределенности системы уравнений. Базисное решение.

Кронекера–Капелли: Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы: rang(A)=rang()

Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.

Теорема 1 Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой

Теорема 2 Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.

Тогда:

1) при r ≠ система несовместна;

2) при r = система совместна, причём, если r = = n, система определённая; если же r = < n, система неопределённая.

! Для того, чтобы система была неопределенной необходимо и достаточно, чтобы ранг совместной системы был меньше числа неизвестных. r = < n

Базисное решение: Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.

Вопрос 24. Пространство решений однородной системы линейных уравнений.

Однородной системой линейных уравнений называется система вида: т.е система, в которой все свободные члены = 0.

Теорема: Любая однородная система совместна, т.к имеет хотя бы одно(нулевое) решение.

Теорема: Однородная система имеет только нулевое решение тогда и только тогда, когда ранг матрицы системы равен числу неизвестных (r(A)=n)

Теорема: если r(A)<n - однородная система имеет ненулевые решения

Теорема: если однородная система n – уравнений с n – неизвестными имеет только нулевое решение, когда матрица системы – неособенная(|A|≠0)

Теорема: однородная система n – уравнений с n – неизвестными имеет ненулевые решения, когда – особенная (|A|=0)

1. Совокупность всех решений однородной системы линейных уравнений образует линейное пространство. Множество решений однородной системы линейных уравнений является векторным пространством

Доказательство. Пусть – однородная система m линейных уравнений с n неизвестными. Тогда решением системы является столбец неизвестных X, который мы рассматриваем как вектор из пространства столбцов высоты n: , где K– поле коэффициентов системы.

Таким образом, множество решений системы есть множество столбцов из пространства столбцов , для которых верно матричное равенство .

2. Размерность пространства решений системы линейных однородных уравнений равна n – r, где n – число неизвестных, r – ранг матрицы системы.