Вопрос 13. Уравнение и свойства гиперболы. Свойства фокальных радиусов с доказательством

Гиперболой называется множество всех точек плоскости, для который модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

В специально подобранной системе координат каноническое уравнение гиперболы имеет вид: ,

где |OA₁|=|OA₂|=a – действительная полуось

|OB₁|=|OB₂|=b – мнимая полуось, F₁(-c;0) и F₂(c;0) – фокусы гиперболы

фокусное расстояние 2с связано с полуосями соотношением: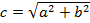

E (эксцентреситет) = . Т.к с>1, то E>1

Расстояние от точки M(x;y), кот принадлежит гиперболе, до фокуса называется фокальным радиусом r₁=Ex-a, r₂=a-Ex.|r2-r1|=2a, разность расстояний постоянна. Асимптоты гиперболы описываются уравнением: y=± x

Отметим следующие свойства гиперболы.

· Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (– a; 0), которые называются вершинами гиперболы.

· Гипербола имеет две взаимно перпендикулярные оси симметрии.

· Гипербола имеет центр симметрии.

· Гипербола пересекается с прямой y = kx при |k|< в двух точках. Если |k|≥ то общих точек у прямой и гиперболы нет.

Date: 2016-02-19; view: 520; Нарушение авторских прав