Переход от одной системы координат в другую

Декартова (прямоугольная) и полярная системы координат на плоскости.

Две взаимно перпендикулярные оси Ox и Oy, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости. Ось Ох называется осью абсцисс, Оу - ординат, а обе оси осями координат. Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называется координатной плоскостью и обозначается Оху

Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и углов

Переход от одной системы координат в другую

Каждой полядной системе координат соответствует вполне определенная прямоугольная система и обратно

Посмотрим как связаны между собой координаты x,y и z какой-нибудь точки M плоскости в обеих системах

Имеем очевидные формулы:

Они позволяют перейти от полярных координат точки M к прямоугольным. Но они же позволяют произвести и обратный переход по формуле:

Из последний 2х равенст вытекает:

3 Ур-е окружности в полярной системе координат:

Пусть требуется найти ур-е окружности, проходящей через полюс, цент кот лежит на полярной оси, а радиус =а. OD- диаметр. Соединим произвольную точку M с O и D. M имеет координаты M(фи;r). Треуг OMD- прямоуг, так как окружность есть геометрическое место вершин прямых углов, опирающихся на ее диаметр. Следовательно r=2a*cos(фи). *Если бы мы выбрали полюс в центре окрудности, r=a, то для всех точек окружности полярный r=а, это равенство и было бы уравнением окружности радиусом a с центром в полясе. Угол фи в это уравнение не входит, оставаясь произвольным

Вопрос 2 Понятие геометрического вектора. Операции с векторами (сумма, умножение на число). Нуль в-р и радиус-вектор, коллинеарные и компланарные вектора. Разложение вектора по базису.

· Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому.

· Суммой двух векторов и называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правильно треугольника).

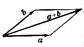· правилом параллелограма: если и приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала и .Отсюда сразу следует, что .

· Правило многоугольника Суммой векторов является большая диагональ, а разностью - малая

· Вектор нулевой длины называется нулевым и обозначается символом

· Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.

· Компланарные вектора - вектор навправления кот параллельны одной и той же плоскости. Копланарны, т.е лежат на одной плоскости перпендикулярно.

· Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены

· Разложением вектора а по базису (e1,e2,e3) называется его запись в виде
a=a1*e1+a2*e2+a3*e3, коэффициенты a1,a2,a3 - коэффициенты разложения вектора a в базисе e1,e2,e

Вопрос 3 Скалярное произведение. Угол между векторами. Признак перпендикулярности и коллинеарности в-в. Длина в-ра.

· Скалярным произведением двух векторов и называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:

· Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

· Условие перпендикулярности векторов

Date: 2016-02-19; view: 1201; Нарушение авторских прав