Формула Тейлора. Разложение элементарных функций по формуле Тейлора

Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении.

Формула Тейлора в общем виде выглядит вот так:

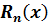– остаточный член формулы Тейлора. Для функций, которые имеют вид многочлена справедливо Для остальных функций существуют некоторые формулы, например:

В форме Лагранжа:

В форме Коши:

Разложение функций по формуле Тейлора:

1)Разложение экспоненциальной функции при a = 0:

2)Разложение функции , при a = 0:

25.Сформулировать свойства функций, имеющих производную в [a;b].Доказать одну из соответствующих теорем, провести её анализ

1.Теорема Дарбу (Вопрос №9). Если функция f(x) определена и непрерывна в [a;b], и если существует конечная производная "x є [a;b], и если f’(a) = A и f’(b) = B, причём A ¹ B, то значение f’(x) сплошь заполняет промежуток между А и В, то есть "С є (A;B) $ c є (a;b): f’(c) = C.

2. Теорема Ролля (Вопрос №4). Пусть функция определена и непрерывна в [a;b], пусть существует конечная производная "x є [a;b], пусть f(a) = f(b). Тогда $ c є [a;b]: f’(c) = 0.

3.Теорема Лагранжа (Вопрос №7). Если функция f(x) определенна и непрерывна в [a;b], и если "x є (a;b) существует конечная производная f’(x), то $ с є (a;b): .

4.Теорема Коши (Вопрос №8) Пусть даны 2 функции, f(x) и g(x), которые:

1)Определены и непрерывны в [a;b].

2)Существует конечные производные f’(x) и g’(x), x є (a;b).

3) g’(x) ¹ 0, x є (a; b).

Тогда, .

Доказательства и анализ всех этих теорем приведены выше в соответствующих вопросах.

26.Сформулировать свойства функций, непрерывных в [a;b].Доказать одну из соответствующих теорем, провести её анализ

1.Первая теорема Вейерштрасса (Вопрос №5). Если функция определенна и непрерывна в [a;b], то она ограничена. (На этом промежутке)

2.Вторая теорема Вейерштрасса (Вопрос №6). Если функция определенна и непрерывна в [a;b], то она достигает своего наибольшего и наименьшего значений. (На этом промежутке)

3.Первая теорема Больцано-Коши (Вопрос №10). Если функция f(x) определена и непрерывна в [a;b], и f(a) * f(b) < 0 (a и b имеют разные знаки), то $ с є (a;b): f(c) = 0.

4.Вторая теорема Больцано-Коши (Вопрос №11). Если функция определена и непрерывна в [a;b] и если f(a) = A и f(b) = B, причём A ¹ B, то "C є (A;B) $ c є (a;b): f(c) = C.

Доказательства и анализ всех этих теорем приведены выше в соответствующих вопросах.

27.Сформулировать свойства числовых последовательностей. Доказать одну из соответствующих теорем, провести её анализ

Последовательность называется возрастающей, если для любого n ∈ N выполняется неравенство a_n < a_n+1.

Последовательность называется убывающей, если для любого n ∈ N выполняется неравенство a_n > a_n+1.

Возрастающие и убывающей последовательности называются монотонными.

Последовательность называется ограниченной сверху, если существует такое число M ∈ R, что a_n≤ M. При этом число M называется верхней границей последовательности.

Последовательность называется ограниченной снизу, если существует такое число m ∈ R, что a_n≥m. Число m называется нижней границей последовательности.

Последовательность называется ограниченной, если она одновременно ограничена и сверху, и снизу.

Остальные свойства сформулированы и доказаны в вопросе №2 (От теоремы 7).