Сформулируйте основные теоремы теории чисел. Докажите одну из них

1.Теорема о существовании иррациональных чисел. Существуют числа, не являющиеся рациональными.

Доказательство:

Не существует рационального числа, квадрат которого равен 2, и, так как число , существует, то из этого вытекает, что существует множество чисел, которое не является рациональным. Для того, чтобы доказать это, нужно доказать, что - число не является рациональным. Предположим обратное: пусть существует такая дробь , такая, что - число целое, q – натуральное (из определения рационального числа, причём p и q – не имеют общих множителей, следовательно, данная дробь - несократимая) и . Из того, что

, тогда p = 2r (r - целое), p – число четное, а q – нечетное (так как общие множители отсутствуют). Теперь подставим значение p в составленное ранее равенство. Получаем: , из чего следует, что q – также четное, что вызывает противоречие в изначальном предположении. Теорема доказана.

2.Теорема о счётности множества рациональных чисел. Множество всех рациональных чисел счетно.

Доказательство: Рассмотрим сначала положительные рациональные числа . Назовем натуральное число p + q высотой рационального числа . Пусть A - множество всех рациональных чисел с высотой, равной n. Множества состоят из конечного числа элементов (рациональных чисел), например

.

Легко видеть, что

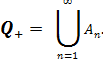
Перенумеруем числа, записанные в фигурных скобках слева направо, выпуская, впрочем, на каждом этапе нумерации те, которые были уже занумерованы на более раннем этапе. В результате получим последовательность

.

Так как рациональных положительных чисел бесконечно много, то мы используем все натуральные числа. Значит, счетно. Далее, очевидно, что счетно. Поэтому все множество рациональных чисел также счетно.

3.Теорема. Открытый отрезок любой длины имеет столько же точек, сколько бесконечная прямая.

4.Лемма о плотности действительных чисел. Каковы бы ни были два вещественных числа a и b, причём a > b, всегда найдется такое вещественное – и, даже, рациональное число r, которое содержится между ними: a > r > b (а, следовательно, и бесчисленное множество таких рациональных чисел)

Доказательство:

Так как a > b, то нижний класс А сечения, определяющего число a, целиком содержит в себе нижний класс В для числа b, не совпадая с В. Поэтому в А найдется такое рациональное число r, которое не содержится в В и, следовательно, принадлежит ; для него: a > r ≥ b

(равенство имело бы место, если бы b было рациональным), но так как в A нет наибольшего числа, то, в случае надобности увеличив r, можно исключить равенство.

5.Лемма о равенстве двух вещественных чисел. Пусть даны два вещественных числа a и b. Если какое бы ни взять рациональное число е > 0,и числа a и b могут быть заключены между одними и теми же рациональными границами:

разность которых меньше e: s’ – s < e, то эти числа a и b - равны.

Доказательство:

Пойдём от противного: пусть, например a > b. По лемме о плотности, между a и b можно вставить два рациональных числа r и r’ > r: a > r’ > r > b. Тогда, для любых двух чисел s и s’, между которыми содержатся a и b, будут выполняться неравенства:

s’> r’ > r > s, откуда s’ – s > r’ - r > 0. В таком случае, разность s’ – s, не может быть меньше числа e, что противоречит условию леммы. Следовательно, предположение неверно и лемма доказана.

6.Теорема Дедекинда. Для всякого сечения в области вещественных чисел существует вещественное число которое производит это сечение. Это число будет либо наибольшим в нижнем классе , либо наименьшим в верхнем классе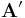

Доказательство: Обозначим через множество всех рациональных чисел содержащихся в , через множество всех рациональных чисел содержащихся в 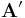. Легко убедится что множества и образуют сечение. Это сечение определяет некоторое вещественное число , которое должно принадлежать одному из множеств или 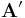. Допустим, оно прирнадлежит , тогда покажем что в этом множестве оно будет наибольшим. Пойдем от противного, допустим это не так, значит в множестве существует число тогда по лемме 1 найдется рациональное число такое что . также принадлежит нижнему классу , а значит принадлежит нижнему классу . Мы пришли к противоречию: рациональное число принадлежащее нижнему классу сечения, определяющего число больше этого числа. Аналогично доказывается, что если попадает в верхний класс 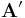, то оно будет там наименьшим. Замечание: Одновременное существование в нижнем классе наибольшего числа, а в верхнем классе 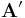наименьшего числа невозможно, что доказывается аналогично как для сечений в множестве рациональных чисел.

7. Теорема о точной верхней и точной нижней гранях числового множества. Непустое множество, ограниченное сверху, имеет точную верхнюю грань, ограниченное снизу — точную нижнюю грань. То есть существуют и такие, что

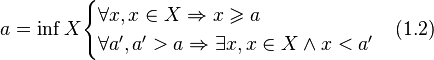
Доказательство:

Доказательство проведём для числового множества .

Для множества ограниченного сверху. Пусть — мажоранта множества , представленная в виде бесконечной десятичной дроби. Множество непусто. Запишем все числа из в виде нормальных десятичных дробей,

.

Множество непусто и ограниченно сверху числом , поэтому существует .

Множество десятичных чисел вида таких, что среди элементов есть число, представление которого в виде бесконечной десятичной дроби начинается с выражения , непусто и состоит не более чем из десяти элементов, поэтому существует .

Допустим, что для некоторого номера построено десятичное число такое, что

1. существует элемент , представление которого в виде бесконечной десятичной дроби начинается с выражения

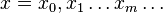2. если x — элемент с представлением , то

.

Обозначим множество десятичных чисел вида , которые служат начальными выражениями для элементов множества . По определению числа на основании свойства 1 множество непусто. Оно конечно, поэтому существует число , обладающее свойствами 1-2 с заменой на , причем появление -ого знака после запятой не влияет на величины предшествующих знаков.

На основании принципа индукции для любого оказывается определенной цифра 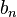и поэтому однозначно определяется бесконечная десятичная дробь

Возьмем произвольное число . По построению числа для любого номера выполняется и поэтому . Следовательно, выполнена верхняя строчка в правой части соотношения 1.1 (смотри формулировку). Следовательно, .

Для множества , ограниченного снизу, рассуждения проводятся аналогично.

Date: 2016-02-19; view: 2055; Нарушение авторских прав