Нагрузки на дисковые шарошки проходческих комбайнов

Дисковой шарошкой называется свободно вращающийся на оси диск с непрерывным клиновым лезвием, который при работе перекатывается по поверхности забоя и внедряется в нее под воздействием усилия подачи.

Дисковые шарошки подразделяются на лобовые и тангенциальные. Основными параметрами, характеризующими схему расположения, принимаются: шаг разрушения H, мм; длина уступа L, мм; глубина борозды или подача шарошки за один оборот исполнительного органа h, мм.

В зависимости от величины отношения L/ H различают три схемы расположения (рис. 3.7): лобовую (рис. 3.7, а) при L/H= 0; тангенциальную (рис. 3.7, в) при L/H ≥2; уступную (рис. 3.7,б) при 0< L/H <2.

Рисунок 3.7 Схемы расположения шарошек относительно забоя

В современных комбайнах значения основных параметров находятся в пределах: h = 2÷30 мм; H =20÷120 мм; L/H 0÷0,5

Рисунок 3.8 Углы, характеризующие установку шарошек на исполнительном органе

Конструкции дисковых шарошек характеризуются следующими параметрами (см. рис. 2.10): диаметром d (мм) и радиусом r (мм) шарошки; углом заострения лезвия σ (градус); радиусом закругления лезвия ρ (мм).

Лобовыешарошки имеют, как правило, симметричное двустороннеелезвие, тангенциальные — несимметричное, обычно одностороннее лезвие.

В современныхпроходческих комбайнах параметры дисковых шарошекимеют следующие значения: диаметр d=150 ÷ 800 мм, чаще всего 250÷350 мм; угол заострения δ = 40 ÷ 90°, по условию прочности лезвия целесообразно выбирать 60—75°; радиус закругления лезвия ρ = 1 ÷5 мм.

Установка тангенциальных шарошек на исполнительных органах комбайнов характеризуется: углом наклона — угол между нормалью к плоскости разрушения и проекцией оси шарошки на плоскость, нормальную к вектору скорости перекатывания; углом разворота шарошки Ψ — угол между нормалью к плоскости разрушения и проекцией оси шарошки на плоскость, нормальную к вектору скорости подачи (рис. 3.8).

Практический интерес представляет разворот, при котором набегающая часть лезвия шарошки ближе к стенке уступа. Разворот в обратную сторону приводит к ухудшению силовых и энергетических показателей процесса разрушения.

Наблюдения за работой лобовых шарошек по песчанику и глинистому сланцу показали, что диск, внедряясь в породу, уплотняет ее поверхностный слой и перемещает его на некоторую глубину без хрупкого разрушения. При увеличении глубины вдавливания образуется уплотненное пылевидное ядро, которое, погружаясь на заданную глубину и одновременно увеличиваясь в размерах, давит во все стороны, что приводит к сколу частиц породы по сторонам диска. Образуется «развал», на дне которого остается нарост — остаток пылевидного ядра.

При увеличении глубины вдавливания щечки диска начинают входить в контакт с породой, причем величина контакта возрастает с глубиной. Сколы породы по длине борозды происходят неравномерно, поэтому щечки находятся в контакте с породой то одной, то другой стороной.

При последовательном виде форма поверхности забоя и характер контакта диска с породой в основном зависели от соотношения шага Н и глубины h вдавливания. При соотношениях H/h ≤5 развал борозды происходил преимущественно в сторону обнаженной' поверхности, на поверхности забоя не образовывались гребешки или они возникали лишь в отдельных местах высотой (0,5—0,8) h.

При H/h> 5—7 после разрушения первого слоя сколы не перекрывали всей поверхности породы. Это происходило только после разрушения последующих слоев. Высота гребешков достигала (3—4) h и более. Например, при шаге 80 мм и глубине вдавливания 2 мм высота целиков составляла 28—30 мм.

Механизм разрушения породы тангенциальной шарошкой во многом аналогичен описанному. Также образуется уплотненное ядро, которое, увеличиваясь в размерах, давит во все стороны с одинаковой силой. При этом происходят сколы частиц уступа. Наличие дополнительной обнаженной поверхности облегчает процесс разрушения, снижает нагрузки и способствует сколу крупных элементов уступа.

Рисунок 3.9 Схема к определению пути скольжения диска шарошки относительно породы

При отношении H/h≤ 7÷8 скалывание уступа на всю величину шага Н происходит, как правило, за один проход шарошки. При больших отношениях H/h могут потребоваться несколько проходов.

Длина уступа L влияет на процесс разрушения при отношении L/H≤ (2÷2,5). При большем соотношении длина уступа перестает влиять на процесс разрушения, усилия стабилизируютсяи разрушение становится таким же, как при тангенциальной схеме.

Во время работы лобовой шарошки ее диск своей передней частью по дуге ОВ вдавливается в породу на некоторую глубину h (рис. 3.9). При движении диска по прямой каждая точка вершины его лезвия описывает относительно породы циклоиды, аточки, расположенные выше вершины, — укороченные циклоиды. При движении по кругу эти циклоиды будут расположенына сферической поверхности.

Путь каждой точки вершины лезвия в контакте с породой за один оборот диска

где dL — дифференциал дуги кривой.

Интеграл этого выражения при прямолинейной траектории

(3.77)

при движении по кругу

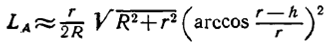(3.78)

где r — радиус диска; R — радиус кривизны траектории.

Угол входа в контакт с породой при движении по прямой (точка В)

(3.79)

Очевидно, что в точке А этот угол равен 90°.

Имея уравнение циклоиды на сфере, не трудно определить углы входа и при движении диска по кругу. Расчеты показали, что в этом случае при R>200 мм и обычно применяемых диаметрах дисков углы входа мало отличаются от вычисленных по формуле (3.79). При r= 100÷300 мм и h = 5÷10 мм угол входа Ө=73÷82°. При таких углах скольжение вершины лезвия относительно породы отсутствует. Скольжение наблюдалось на боковых поверхностях лезвия и нижней части щечек. Эти поверхности изнашиваются, чем и объясняется самозатачиваемость дисков.

Вычисления по формулам (3.77) и (3.78) показывают, что при применяемых размерах дисков и глубине вдавливания h до 15 мм путь каждой точки вершины лезвия в контакте с породой за один оборот диска

(3.80)

Вследствие хрупкости горных пород путь скольжения точек диска по породе будет еще меньше:

(3.81)

где K_т<1 — коэффициент, определяемый из опыта.

Путь скольжения L_T (%), приходящийся на единицу пути диска по забою:

(3.82)

Вычисления по последней формуле показали, что L_T< 1÷2%.

Следовательно, путь скольжения дисковой шарошки в десятки раз меньше, чем у резцов, и уменьшается с увеличением диаметра диска.

Скорости точек вершины лезвия относительно породы наибольшее значение имеют в точке В: при движении диска по прямой

при движении диска по кругу

где v — окружная скорость диска.

При перемещении точки В в положение А ее скорость снижается до нуля. Подсчет показывает, что скорость ν_Р в несколько раз меньше скорости диска v. Скорости точек, расположенных на диске выше линии В — В' еще меньше. Это обстоятельство благоприятно сказывается на тепловом режиме шарошек и выгодно отличает их от резцов.

При движении по кругу точки вершины лезвия внедряются в породу на глубину h и одновременно перемещаются к центру кривизны траектории на величину (см. рис. 3.9)

(3.83)

которую называют радиальным путем скольжения диска за один его оборот. Путь любой другой точки диска меньше L_r. Применительно к рассматриваемым условиям L_r на один-два порядка меньше L_А; его следует учитывать при траекториях с радиусом кривизны R<300 мм.

Расчет нагрузок на дисковые шарошки излагается авторами по методике Донгипроуглемаша с учетом результатов последующих исследований, выполненных в ИГД им. А. А. Скочинского.

На лезвие шарошки при ее перекатывании по забою действует реакция забоя, распределенная по параболической кривой (рис. 3.10). Равнодействующая распределенных сил Р расположена под углом φ к оси у и может быть разложена на три составляющие: Z — усилие перекатывания, У — усилие подачи и X — боковое усилие.

Площадь контакта шарошки с породой ограничивается длиной дуги ОА или ее проекции l на ось OZ и средней высотой контакта h_к, которая принимается по аналогии с разрушением углей,

(3.84)

Общий вид формулы для определения равнодействующей Р (Н) без учета сил трения

где Р_к — контактная прочность породы, МПа, принятая в качестве критерия сопротивляемости породы разрушению; F_K — условная площадь контакта шарошки с разрушаемой породой, мм²,

(3.86)

Рисунок 3.10 - Схема сил на лобовой дисковой шарошке

Расчетная ширина площади контакта шарошки с породой b зависит от формы диска и величины подачи за оборот исполнительного органа. Для неизношенной шарошки:

(3.87)

Для среднезатупленной шарошки величина параметра износа принимается в зависимости от вида шарошки: лобовая — b = 10÷11 мм, тангенциальная — b = 15÷18 мм.

Коэффициент А представляет собой соотношение среднего значения сопротивления породы вдавливанию шарошки и контактной прочности породы. Его величина была определена из экспериментов согласно соотношению

Здесь Р_э, Z_э и Y_э — экспериментальное значение силы соответственно реакции забоя, перекатывания и подачи; К_Hh — коэффициентобнажения забоя, учитывающий влияние соседних шарошек иповторность разрушения,

где H и h — в миллиметрах; K_LH — коэффициент вида разрушения;учитывает, при какой схеме расположения — лобовой, тангенциальной или ступенчатой — работает шарошка,

(3.89)

При тангенциальной схеме, когда L/H >2, следует принимать K_LH для значения L/Н= 2.

Средняя сила перекатывания, Н,

Угол, определяющий положение равнодействующей силы реакции забоя,

Коэффициент, учитывающий положение равнодействующей cилы реакции забоя,

При Н/ h <3 следует принимать Кj для Н/ h =3; при L/H >2 следуетпринимать Кj для L/H = 2.

В формуле (3.89) и далее Н, h и L — в миллиметрах.

Угол контакта ф⁰_m шарошки с породой

(3.93)

Значения сил перекатывания Z, подачи Y и боковой X определяются в соответствии со схемой, представленной на рис. 3.10:

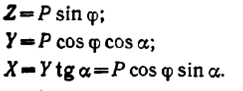
Значения угла положения сил реакции породы X получены на основании анализа экспериментальных данных.

В общем случае угол a определяется по формуле

При тангенциальной схеме (L/H ³2) и уступной (0 < L/H <2), когда величина Н/ h достигает значительных величин, угол a соответствует сколу на свободную поверхность и определяется по формуле

Date: 2016-02-19; view: 2213; Нарушение авторских прав