Методы определения нагрузок на режущих инструментах

Основа современных методов - отыскание экспериментальным путем инвариантных корреляционных соотношений между показателями какого-либо из горнотехнологических критериев свойств породы и процесса разрушения. При этом важно выбрать такой критерий, который обеспечивал бы по возможности большую тесноту корреляционной связи. Отыскание корреляционных соотношений не исключает аналитического описания отдельных сторон процесса резания. Это тем более необходимо, что факторы, характеризующие геометрические параметры инструментов (точнее, те из них, которые при своем изменении не вызывают качественных изменений процесса разрушения), могут находиться с действующими на инструмент усилиями в функциональной связи, обусловленной известными законами механики.

Имея в виду сказанное выше, схему взаимодействия резца с породой можно представить следующим образом.

В рабочем состоянии на резце образуются две площадки: передняя F_п, которой он снимает слой породы, и торцевая F_зат, которой он давит на забой реза (рис. 3.2).

Рисунок 3.2 – Схема определения рабочих площадей резца.

Передняя площадка резца (3.2)

где — высота контакта резца с породой по передней поверхности; b_p — ширина режущей кромки, измеряемая на высоте ; — коэффициент формы, учитывающий влияние формы режущей кромки и передней поверхности на величину передней площадки.

В процессе резания высота контакта циклически изменяется от нуля до некоторого максимального значения. Максимальная высота контакта 0а= соответствует моменту скалывания крупного элемента стружки в случае, если усилие скалывания становится равным усилию дробления, Р_cк = Р_Д. Этому условию соответствует равенство средних удельных сопротивлений на единицу ширины режущей кромки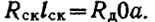

где R_ск и R_д — сопротивление породы соответственно скалыванию и дроблению; τ — угол скалывания.

Принимая и приближенно считая, что высота контакта изменяется по линейному закону, получаем

(3.3)

Подставляя полученные значения в формулу (3.2), получаем

(3.4)

Торцовую площадку принимают равной проекции площадки износа на плоскость резания и определяют измерением. Она пропорциональна проекции ее длины на плоскость резания:

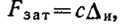(3.5)

где с — коэффициент пропорциональности, определяемый экспериментально; — проекция длины торцовой площадки на плоскость резания, измеряемая обычно по оси резца. Она называется линейным износом по задней грани.

Схема сил на резце (рис. 3.3) составлена, исходя из следующих допущений: распределенные силы на рабочих площадках заменены их результирующими; силы сопротивления приложены нормально к рабочим площадкам; площадка износа совпадает с траекторией ее движения. Линия WW представляет касательную к траектории движения точки А режущей кромки резца.

Рисунок 3.3 – Схема сил на резце

Со стороны породы на резец действуют нормальные силы: на передней и торцовой площадках соответственно N _п и N₃ на боковых гранях N_бл и N _бп. Нормальным силам соответствуют вызванные ими силы трения . Для преодоления этих сил к резцу приложены со стороны машины усилия: резания Z, подачи Y и боковое X.

Проектируя данную систему сил на ось z, получаем выражение для определения усилия резания:

(3.6)

Суммируяпроекции сил на ось y, находим усилие подачи

(3.7)

Боковая сила

(3,7)

Экспериментальное определение боковых сил затруднительно, поэтому обычно вводят соотношение

,

где — коэффициент сопротивления резанию.

Усилие подачи на боковых кромках незначительно, и в первом приближении им можно пренебречь

Нормальные усилия на площадках резца

Подставляя в формулы (3.6) и (3.7) приведенные выше соотношения, а также значения нормальных сил, выраженные через рабочие площадки и действующие на них давления, получаем после преобразований:

(3,8-3,9)

Нагрузка dN, приложенная нормально к элементарной площадке контакта инструмента с породой dτ (рис. 3.4),

где Р_уд — средняя удельная нагрузка на поверхности контакта инструмента с породой.

Рисунок 3.4 – Схема определения проекции элементарной нагрузки на оси координат

Если плоскость тп касательна к площадке dτ и составляет угол р с координатной плоскостью, то элементарную площадку можно выразить через ее проекцию на эту плоскость. Тогда

Проекция элементарной нагрузки на какую-либо ось координат, например у,

Соответственно

(3.10)

Очевидно, что

(3.10)

и т.д.

Таким образом, результирующая составляющая элементарных нормальных сил, действующих на данную поверхность, равна произведению средней удельной нагрузки на площадь проекции этой поверхности на координатную плоскость, нормальную к этой составляющей.

Применение этого правила значительно облегчает задачу получения расчетных формул: контактные площадки можно определять вычислением или измерением плоских фигур; удельные нагрузки — поиском корреляционных соотношений их с горно-технологическими свойствами породы.

В соответствии с этим правилом в формуле (3.2) ширина режущей кромки b равна проекции на плоскость ху линии, проведенной на передней грани на высоте контакта h_k; в формулах (3.8) и (3.9) F_зат=S_XZ, R_Д,=R _уд, R _ск=Я'_уд.

Характер изменения нагрузок на инструменты зависит от свойств горных пород (рис. 3.5).

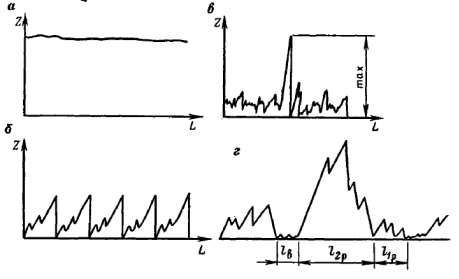
Рисунок 3.5 - Осциллограммы усилий резания: а – идеально пластичная горная порода; б – идеально хрупкая горная порода; в – реальная неоднородная горная порода; г - типичная осциллограмма процесса резания угля

К идеально пластичным горным породам близки пластичные глины и мягкие грунты; близкие по характеру к идеально хрупким породам осциллограммы наблюдались при резании каменной соли. На осциллограмме процесса резания угля различаются: участки резания угля , прорезания твердых включений передового выкола lв.

Процесс разрушения реальной горной породы — стохастический, поэтому для получения достоверных данных о закономерностях изменения нагрузок пользуются методами теории вероятностей и математической статистики. При этом нагрузка характеризуется совокупностью характеристик: видом закона распределения, средней величиной, показателем изменчивости (дисперсией, средним квадратическим отклонением), числом циклов нагружения и максимальной величиной.

Значение первых четырех характеристик позволяет определять эквивалентные нагрузки, по которым рассчитывают инструменты на усталостную прочность (долговечность). Максимальные нагрузки нужны для расчетов на статическую или ударную прочность.

Экспериментально установлено, что закономерности изменения нагрузок для различных процессов разрушения горных пород характеризуются каким-либо из следующих законов распределения: нормальным; усеченным нормальным; Вейбулла и гамма-распределением.

Плотность распределения при нормальном законе

(3.11)

Нормальный закон справедлив для распределения исследуемого признака в границах ± . Поскольку нагрузка Р есть величина положительная, рекомендуется применять усеченное нормальное распределение

(3.12)

при а<р<b. В этом выражении параметр

При Р>2σ параметр С практически не отличается от единицы и замена усеченного распределения обычным нормальным правомерна.

Закономерности измерения нагрузок на инструменты при резании угля согласуются с законом гамма-распределения:

(3.13)

где — параметры распределения,

В некоторых случаях при разрушении горных пород распределение усилий подчиняется закону Вейбулла:

(3.14)

где параметр определяет масштаб, а параметр k — асимметрию и эксцесс распределения.

В формулах (3.11) — (3.14): Р — нагрузка (текущая); — среднее квадратическое отклонение; — математическое ожидание, которое принимают равным средней (из опыта) нагрузке — интеграл вероятностей; D — дисперсия.

Максимальная нагрузка

(3.15)

где k_M.П — коэффициент максимальной перегрузки.

Пропорциональность максимальных и средних нагрузок установлена экспериментальными исследованиями.

Перегрузки, при которых нарушается прочность инструмента, возникают довольно редко. Поэтому при грубом определении под максимальной понимают обычно максимальную пиковую нагрузку, выявленную при обработке осциллограмм процесса резания (см. рис. 3.5). Отсутствие более точных заний компенсируют при расчетах увеличением коэффициента запаса прочности.

Частота колебаний нагрузки Р _пик оценивается частотой возникновения пиковых нагрузок на 1 м пути резания или в единицу времени и определяется из осциллограмм.

Среднее поперечное сечение стружки

(3.16)

где F _cp— сечение стружки, см²; G — масса породы, отделенной резцом на пути l, кг; — плотность породы в плотном теле, кг/см³.

Условное напряжение разрушения

Условное напряжение разрушения (кПа) численно равно удельной энергии резания (Дж/см³) и связано с удельной энергоемкостью (кВт*ч/м³) коэффициентом α _w :Дж/см³ = α _w (кВт*ч/м³), откуда a_w = 0,00272.

Тогда удельная энергоемкость W (Дж/м³) процесса разрушения:

W=0,00272Z_cp/F_cp. (3.17)

Методы получения формул для расчета средних нагрузок. Формулы (3.8) и (3.9) дают представление о влиянии на нагрузку резца некоторых факторов только с качественной стороны. Они не учитывают влияния схемы резания, масштабного фактора, развала реза, горно-геологических условий и др. Свойства породы представлены в этих формулах в неявном виде и требуется установить корреляционные соотношения R_Д, R_ск и горнотехнологических критериев. Величины F _зат, h и могут быть измерены или вычислены с достаточной точностью. В целом формулы представляют собой сложные многофакторные выражения, в которых одна группа факторов связана с нагрузкой корреляционными соотношениями, а другая группа факторов — функциональными связями. При экспериментальном отыскании таких соотношений и связей применяют известное правило, согласно которому многофакторная функция может быть представлена как произведение частных функций:

f (х, у, z) = f₁ (х) f₂ (у) f ₃ (z)... (3.18)

При отыскании каждой частной функции это правило может быть использовано при условии сохранения остальных факторов в процессе опыта постоянными величинами. Обстоятельства каждого опыта должны быть тщательно проанализированы с целью выявления и устранения возможного скрытого влияния какого-либо фактора. Например, скорость резания может влиять на результаты опыта как непосредственно, так и через сопутствующие ей высокие температуры. Следовательно, скорость резания должна быть выбрана в таких пределах, чтобы влияние теплового фактора было устранено или применено эффективное охлаждение.

Представим выражения (3.8) и (3.9) в виде:

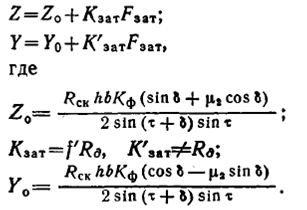(3.19-3.22)

Силы Z₀ и Y₀, представляющие нагрузки соответственно на передней и торцовой площадках, иногда называют нагрузками на остром резце. Для определения этих нагрузок опыты ставят на технически острых резцах, толщина режущих кромок которых составляет по замерам 0,05—0,10 мм. Влияние затупления может быть установлено замерами нагрузок на резцах с различными F _зат и последующими вычислениями по схеме: K_зат = Z-Z₀/F _зат; К' _зат = Y — Y_o/F _зат; f ' = К_зат/К'_зат.

Необходимое число опытов следует устанавливать статически, исходя из значения характерного для исследуемого фактора коэффициента вариации K _вар и требуемой степени точности результата K_доп. Зная значение коэффициента вариации для исследуемого фактора и задаваясь значением надежности, можно определить требуемое число опытов по соотношению K_доп / K _вар.

Примем в выражении (3.8)

(3.23)

Коэффициент К_У отражает влияние угла резания на нагрузку резца. Это влияние тесно связано с влиянием трения по передней грани и угла скалывания породы.

При экспериментальных исследованиях влияния угла резания определяют не абсолютные, а относительные значения коэффициента К_у. При этом за эталонные принимают значения при каком-то выбранном значении угла резания.

На рис. 3.6 приведены две зависимости коэффициента

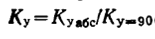(3.24)

от угла резания, где К_У = 90 — значение коэффициента К_{У абс} при угле резания 90°. Экспериментальные данные, полученные в результате обобщения многих исследований А. И. Бероном, А. С. Казанским и Л. И. Бароном и Л. Б. Глатманом, нанесенные на график, весьма близки к расчетным кривым, построенным при усредненных значениях . Расчеты показали, что при других значениях , имеющих место на практике, «ножницы» между кривыми 1 и 2 раскрываются или сужаются, включая в себя соответствующие значения коэффициентов К_у.

Date: 2016-02-19; view: 1563; Нарушение авторских прав