Динамика процессов при вращательном бурении шпуров

Как известно, математические модели динамики машин базируются на преобразованиях уравнения Лагранжа. Применительно к бурильной установке БУЭ-1М принятые эквивалентные схемы систем подачи и вращателя согласно ранее выполненным исследованиям можно представить двухмассовыми системами (рис. 7.1), которые без учета диссипативных потерь описываются следующими уравнениями:

(7.1)

где T, П — кинетическая и потенциальная энергия системы;; Уб.м, У* фш, фи — обобщенные координаты линейных и угловых: перемещений масс; Рп — усилие подачи; RH — усилие сопротивления резца внедрению; Мш — момент, развиваемый двигателем вращателя, приведенный к шпинделю; Ми — момент сопротивления на резце.

Составим выражения для определения кинетической (Т) к потенциальной (П) энергий системы:

Таблица 7,1

где тб.м, Шн, /ш, /и—приведенные к шпинделю и к инструменту массы и моменты инерции; Сп, С к—приведенные к штанге продольная и крутильная жесткость.

Подставив выражения (7.2) и (7.3) в систему уравнений <(7.1) и произведя дифференцирование, получим систему уравнений, описывающих движение инструмента и вращателя бурильной установки:

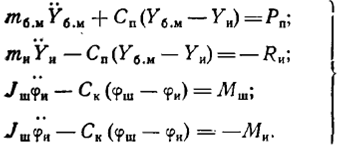(7.4)

Колебания усилия подачи и крутящего момента на резце при вращательном бурении, как показывают осциллограммы, не являются гармоническими. Поэтому решение системы (7.4) возможно методами численного интегрирования на ЭВМ.

Значения параметров, входящих в уравнения (7.4), приведены в табл. 7.1 для бурильной установки БУЭ-1М.

Момент, развиваемый электродвигателем вращателя:

Где — критический момент, Н*м.

Критическое скольжение

где S_ном =0,02662 — номинальное скольжение; α=1—для двигателей нормального исполнения.

Таблица 7.2

Значения рассчитанных параметров буровых штанг приведены в табл. 7.2.

Остальные значения параметров: согласно методу Рэлея,

позволяющего массу штанги представить как распределенную, к массе (моменту инерции) шпинделя и к массе (моменту инерции) инструмента необходимо прибавить 1/з массы (момента ■инерции) штанги. Тогда,.при Lm=3,5 м, / = 1,271 кг-м2; /и = =9,5-10~4 КГ'М2; /Иб.м = 216,8 кг; ти=6,8 кг.

На основании анализа кинограмм при строгании и бурении •с различной толщиной стружки и элементов сколов была предложена расчетная схема к математическому описанию процесса резания резцом единичной ширины. В отличие от предшествующих, рассматривающих резание как циклический двухстадийный процесс, характеризующийся дроблением и последующим сколом только крупных элементов, предложенная расчетная схема предусматривает один, два и более промежуточных мелких сколов к вновь образованной поверхности. Угол скола любого элемента к ближайшей поверхности обнажения незначительно отличается от угла скола породы т, а отношение высоты контакта стружки к длине линии скола: hCr/l=K есть величина постоянная. При этом скалывание элементов происходит циклически по концентрическим траекториям с шириной полосы, равной (0,7—0,8) длины скола крупного элемента. Недостаток такой схемы состоит в том, что она не отражает процесс формирования нагрузок при продольных колебаниях штанги. В НПИ предложена более совершенная расчетная схема резания горной породы резцом единичной ширины, в которой толщина стружки вычисляется как разность между координатами предыдущего и текущего положений забоя (рис. 7.2). Ориентация действующих на переднюю грань и площадку затупления сил (dN „, dTn, dN3, dT3) определяется с помощью кинематических параметров (см. 2.3). Полученные значения элементарных сил затем интегрируются по всем режущим кромкам, выдавая в результате мгновенные значения усилия Rn й моменты Ми сопротивлений на резце.

Использование этого метода весьма трудоемко, так как связано с разработкой сложных алгоритмов и большими затратами машинного времени. Кроме того, аналитические описания последовательности формирования сколов на забое и миграции мгновенной оси вращения резца пока еще не обладают достаточной для адекватного воспроизведения точностью.

Поэтому в расчетной схеме авторами был принят другой подход, основанный на установлении закономерностей процесса формирования нагрузок в целом на резце без влияния на него динамики системы. Суть подхода заключается в том, что для заданной конструкции бурового резца находят зависимости усилия R„ и момента сопротивления Мя от угла поворота <ри и описывают их посредством средних, вычисленных по формулам

(3.140) и (3.144), и коэффициентов, учитывающих только динамику процесса разрушения пород буровым резцом:

Date: 2016-02-19; view: 587; Нарушение авторских прав