Методические указания к решению задач

1. Задача 1.

В задачах №1 и №2 требуется найти положение главных центральных осей и вычислить значения главных центральных моментов инерции.

Главными центральными называются оси, проходящие через центр тяжести, относительно которых осевые моменты инерции имеют экстремальные значения, а центробежный момент инерции обращается в ноль. Моменты инерции относительно главных осей называются главными моментами инерции и обозначаются J₁=J_max, J₂=J_min.

Ось симметрии и любая ось, ей перпендикулярная, составляют пару главных осей.

В Задаче № 1 необходимо найти положение центра тяжести сечения и провести через центр тяжести главные центральные оси Оx и Оy. Далее с помощью зависимостей между моментами инерции относительно параллельных осей необходимо найти осевые моменты инерции J_x, J_y и по их значениям определить, какая из осей является осью максимального момента инерции, а какая осью минимального момента инерции, например J_x=J_1, , J_y=J₂.

2. Задача 2.

В Задаче №2 сечение не имеет осей симметрии. Поэтому величины главных моментов инерции и положение главных центральных осей определяются по формулам:

где α₁, α₂ - углы, определяющие положение главных осей; J_x, J_y, J_xy - осевые и центробежный моменты инерции относительно произвольных осей, проходящих через центр тяжести.

Решение задачи №2 проводится в следующем порядке:

а. Сечение разбивается на элементы, для которых вычисляются необходимые геометрические характеристики - площади и моменты инерции относительно осей, проходящих через центры тяжести элементов;

б. Находится положение центра тяжести сечения.

в. Через центр тяжести проводятся произвольные оси Оx,Оy и при помощи зависимостей между моментами инерции относительно параллельных осей находятся осевые J_x, J_y и центробежный J_xy моменты инерции.

г. По формулам (1) вычисляются величины главных моментов инерции и находится положение главных осей сечения.

В графической части работы необходимо начертить в масштабе сечение и указать основные размеры. Представить разбиение сечения на простые элементы, через центры тяжести которых провести оси O_ix_i , O_iy_i и показать главные центральные оси Ox,Oy. При решении следует отдельно начертить элементы, входящие в состав сечения, для которых необходимо записать геометрические характеристики с учетом положения в сечении и принятой системы координат.

3. Задача 3. При решении задачи № 3 расчет стержня ступенчато постоянного сечения следует начинать с определения опорной реакции с использованием уравнения равновесия:

,

а начало координат расположить в опорном сечении.

Эпюра продольных сил N строится при помощи метода сечений, для чего необходимо показать характерные сечения по длине стержня. В отсеченной части стержня должна быть показана положительная (растягивающая) продольная сила. Контроль правильности построенной эпюры N следует проводить с использованием дифференциальной зависимости:

.

На участках, где q(x) =0, продольная сила N должна быть постоянной, а на участках, где q(x) = const, продольная сила изменяется по линейному закону.

Эпюра нормальных напряжений строится с использованием формулы:

.

Значения N и σ, полученные в начале и конце характерных сечений, откладываются от оси стержня с указанием знака; производится штриховка эпюр.

Эпюра осевых перемещений u(x) строится с использованием формулы:

Для определения осевого перемещения в сечении с координатой «х» необходимо вычислить площадь эпюры нормальных напряжений между опорным сечением и рассматриваемым сечением. Для определения абсолютного удлинения стержня необходимо вычислить всю площадь эпюры нормальных напряжений:

При оформлении графической части работы на листе формата А4 необходимо изобразить стержень с геометрическими размерами и нагрузками, указать характерные сечения и в выбранном масштабе построить эпюры продольных сил N, нормальных напряжений σ и осевых перемещений u(x).

4. Задача 4. В задаче № 4 необходимо определить усилия N₁ и N₂ в стержнях 1 и 2 по методу предельных состояний от действия расчетной нагрузки:

,

где Р_н - нормативная нагрузка, γ_f - коэффициент надежности по нагрузке.

Так как задача является статически неопределимой и уравнений равновесия недостаточно для определения неизвестных усилий, то для решения задачи необходимо рассмотреть геометрическую схему деформаций и получить зависимость между абсолютными удлинениями Δl₁, Δl₂: Δl₁ = k₁ Δl₂.

Абсолютные удлинения стержней Δl₁, Δl₂ нужно выразить через усилия в стержнях N₁, N₂ и получить дополнительное уравнение, связывающее между собой усилия в стержнях N₁ = k₂N₂, где k₂ - коэффициент, зависящий от геометрических параметров системы и соотношения площадей стержней F₂ / F₁.

Для определения усилий в стержнях 1 и 2 следует воспользоваться уравнением равновесия ΣМ_А = 0 и уравнением N₁ = k₂N₂ .

Подбор сечений стержней 1 и 2 производится по формулам:

После определения площадей сечений необходимо проверить заданное отношение площадей стержней F₂/F₁. Изменив площади поперечных сечений при невыполнении заданного отношения F₂/F₁, подбираем по сортаменту сечения стержней 1 и 2 в виде двух равнобоких уголков.

Проверка выполнения условий прочности производится по формулам:

Абсолютные удлинения определяются по формулам:

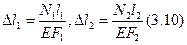
При выполнении задачи принимается упрощенная диаграмма зависимости между напряжениями σ и деформациями ε (диаграмма Прандтля). Согласно диаграмме Прандтля при напряжениях в стержнях, равных пределу текучести σ_т деформации неограниченно возрастают.

Для определения нагрузки Р_т, при которой в системе возникают первые пластические деформации, необходимо согласно проведенному расчету установить наиболее напряженный стержень, в котором при возрастании нагрузки возникнут напряжения, равные пределу текучести, и соответствующее усилие N = σ_тF. Тогда усилие во втором стержне определится из равенства N₁ = k₂N₂, а нагрузка Р_т - из уравнения равновесия системы ΣМ_А = 0.

Для определения разрушающей нагрузки Р_разр необходимо рассмотреть предельное состояние системы, при котором в обоих стержнях возникают напряжения, равные пределу текучести σ₁ = σ_т, σ₂ = σ_т и соответствующие усилия N₁^т = σ_тF₁, N₂^т = σ_тF₂ .Разрушающая нагрузка определяется из уравнения равновесия системы в предельном состоянии ΣМ_А = 0.

В графической части работы необходимо на листе формата А4 изобразить схему статически неопределимой системы с необходимыми геометрическими размерами, показать нагрузку Р, горизонтальную и вертикальную составляющие опорной реакции в шарнире А и усилия в стержнях N₁, N₂; показать геометрическую схему деформации; начертить диаграмму Прандтля; изобразить схему стержневой системы с необходимыми геометрическими размерами, показать нагрузку Р_разр, усилия в стержнях N₁^т и N₂^т, действующие в предельном состоянии.

5. Задачи 5, 6. Расчет статически определимых стержней на изгиб следует начинать с определения опорных реакций из уравнений статики, которые нужно составлять таким образом, чтобы в каждое из них входила бы одна опорная реакция. Расчетную схему балок с промежуточными шарнирами по схемам

следует представить в виде поэтажной схемы и определить опорные реакции для несомой и несущей балок.

Эпюры внутренних усилий - изгибающих моментов М, поперечных Q и продольных сил N строятся с использованием метода сечений устанавливая их законы изменения в пределах рассматриваемых участков стержня, или вычисляя значения М, Q, N на границах участков и следуя следующим правилам:

1.На участках, где q = 0, поперечная сила Q = const, а изгибающий момент M изменяется по линейному закону.

2.На участках, где q = const, поперечная сила Q изменяется по линейному закону, а изгибающий момент М - по квадратной параболе, обращенной выпуклостью в сторону действия нагрузки q.

3.В сечениях, где Q = 0, изгибающий момент М может иметь экстремум.

4.В точке приложения сосредоточенной силы эпюра Q имеет скачок,

равный по величине приложенной в этой точке силе, а эпюра моментов М имеет излом.

5.В точке приложения сосредоточенного момента эпюра М имеет скачок, равный по величине приложенному моменту.

В графической части задания необходимо на отдельном листе формата А4 изобразить схему стержня с геометрическими размерами и приложенными нагрузками, а также определенные из уравнений статики опорные реакции. Для горизонтальных балок под схемой стержня в масштабе вычерчиваются эпюры изгибающих моментов М и поперечных сил Q. Для составных балок следует показать также поэтажную схему.

Для консольного ломаного стержня и рамы вычерчиваются геометрические схемы с указанием размеров и нагрузок и показываются оси стержня, на которых строятся эпюры изгибающих моментов М, поперечных сил Q и продольных сил N.

Эпюры зашриховываются прямыми линиями, перпендикулярными к оси стержня и указываются знаки внутренних усилий. Также приводятся необходимые расчеты по определению опорных реакций и вычислению значений внутренних усилий в рассматриваемых сечениях стержней.

При решении задачи № 2 следует показать однопролетную двухконсольную балку и соответствующие эпюры поперечных сил Q и изгибающих моментов M.

Сечение балки в виде стального прокатного двутавра подбирается по требуемому из условия прочности моменту сопротивления:

W_z > M_расч/γ_cR( 11), где M_расч = М_нормγ_f( 12)

расчетное значение наибольшего изгибающего момента, γ_f - коэффициент надежности по нагрузке, γ_c - коэффициент условий работы, R - расчетное сопротивление по пределу текучести. По величине требуемого момента сопротивления по сортаменту прокатных профилей подбирается номер двутавра, для которого выписываются необходимые геометрические характеристики: h - высота двутавра, b - ширина полки, d - толщина стенки, t - толщина полки, J_z - момент инерции, W_z - момент сопротивления сечения и статический момент S_z половины сечения. Двутавровое сечение с указанными размерами следует начертить в масштабе и и построить рядом с сечением эпюры нормальных σ и касательных τ напряжений по формулам для сечений с наибольшим изгибающим моментом и с наибольшей поперечной силой. Нормальные и касательные напряжения определяются по формулам

,

где М и Q - расчетные значения изгибающего момента и поперечной силы в рассматриваемых сечениях.

Проверка условий прочности по нормальным и касательным напряжениям производится по формулам:

,

где W_z - момент сопротивления сечения, S_z - статический момент половины сечения относительно нейтральной оси.

4. Основные законы и формулы

Date: 2016-02-19; view: 655; Нарушение авторских прав