
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Моменты инерции простых сечений
|
|
Прямоугольник.
Моменты инерции относительно осей Оx, Оx1, Оy, Оy1:
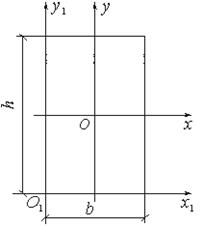
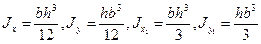
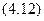 .
.
Произвольный треугольник.
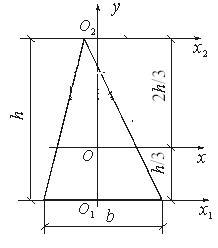
моменты инерции относительно осей Оx, О1x1 и О2x2,:
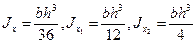
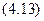
Прямоугольный и равнобедренный треугольники.
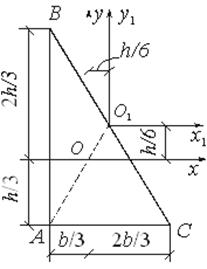
Для прямоугольного треугольника определим центробежный момент инерции Jxy относительно центральных осей Ox и Oy, параллельных катетам:
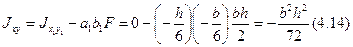
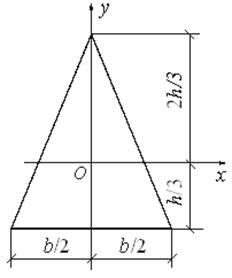
Момент инерции равнобедренного треугольника относительно оси
симметрии Оy:
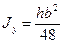
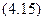
Круг. Полярный момент инерции круга:
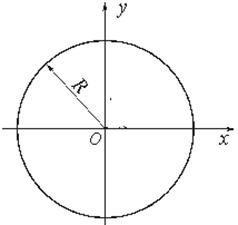
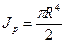
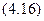
Учитывая, что для круга Jx = Jy и полярный момент согласно равен сумме двух осевых моментов, получим:
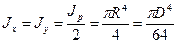
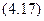
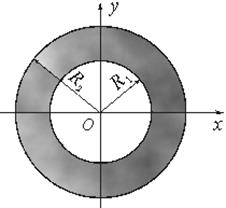
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R2 и R1:
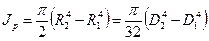
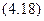
Полукруг.
Относительно осей O1x1 и O1y1, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:
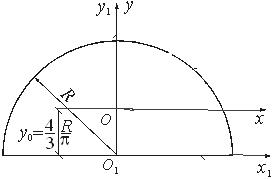
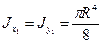
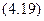
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:
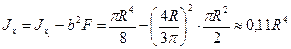
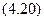
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.
Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).
Далее рассмотрены примеры задач.
5. Примеры решения задач
Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах. 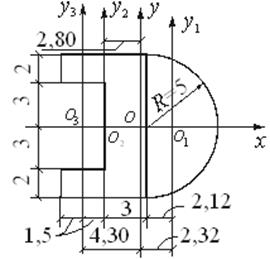
Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6x10 см, прямоугольный вырез с размерами 3x6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.
Для полукруга по формулам (2.21) и (2.22) имеем:
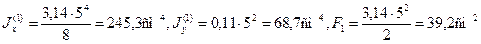
Положение центра тяжести О1 полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).
Для прямоугольника и прямоугольного выреза по формулам (2.13) получим
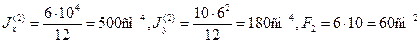
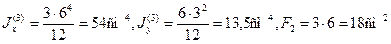
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см2.
Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O2y2. Тогда получим
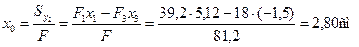 .
.
Отложим эту величину от оси О2y2 вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а1 = 2,32 см, а2 = – 2,80 см, а3 = – 4,30 см.
По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:
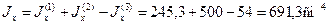
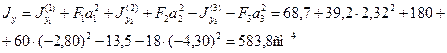
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.
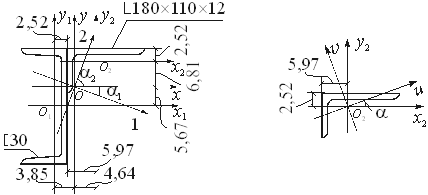
Выпишем геометрические характеристики сечения швеллера:
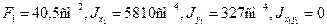
Геометрические характеристики сечения неравнобокого уголка:
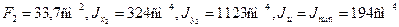
Величину центробежного момента инерции уголка 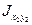 (в сортаменте она не приведена) определим по второй из формул (2.11):
(в сортаменте она не приведена) определим по второй из формул (2.11):
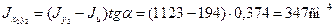 ,
,
где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох2, величина которого приведена в сортаменте.
Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см2.
Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О1x1 и О1y1. Тогда по формулам (2.5) получим
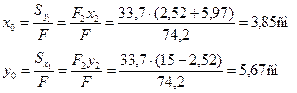
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:
a1= – 3,85 см, b1 = – 5,67 см, а2 = 4,64 см, b2 = 6,81 см.
Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.
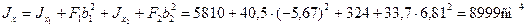
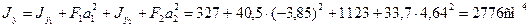
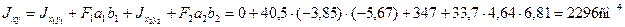
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох:
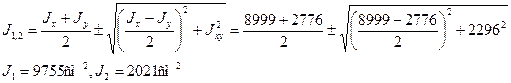
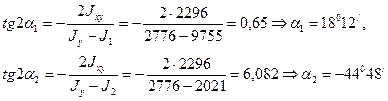
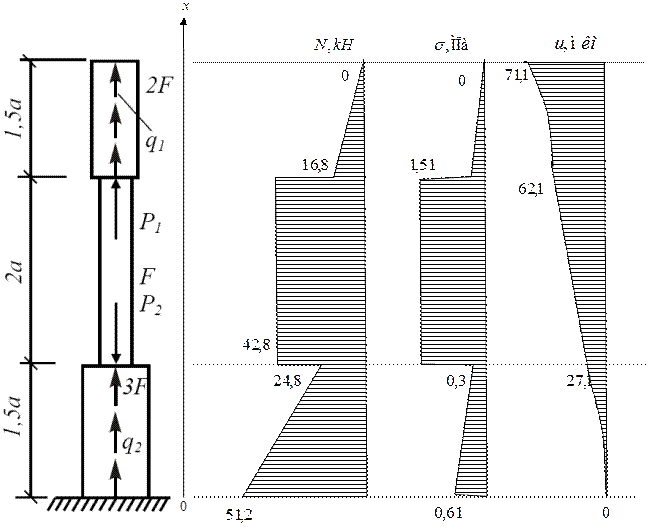
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:
1.Определить опорную реакцию в месте закрепления стержня.
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
| a, м | F, см2 | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | Е, МПа |
| 0,8 | 2,0·105 |
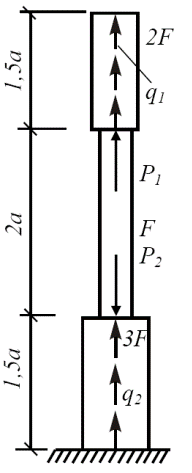
1. Составим уравнение равновесия: 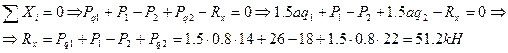
2. Вычислим значения продольных сил:
Участок 1: 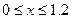
При 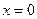 ;
; 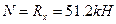
При  ;
; 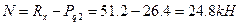
Значение продольной силы линейно уменьшается
Участок 2: 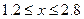
При  ;
; 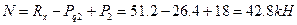
При 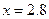 ;
; 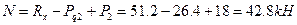
Значение продольной силы не изменяется
Участок 3: 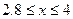
При 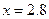 ;
; 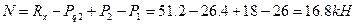
При 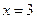 ;
; 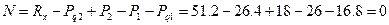
Значение продольной силы линейно уменьшается.
Найдем величины нормальных напряжений в характерных сечениях:
Участок 1: 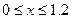
При 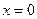 ;
; 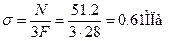
При  ;
; 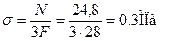
Участок 2: 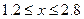
При  ;
; 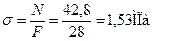
Участок 3: 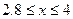
При 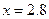 ;
; 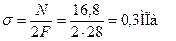
При 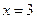 ;
; 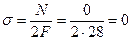
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:
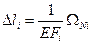 , где
, где 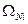 - площадь под эпюрой продольных сил на каждом участке.
- площадь под эпюрой продольных сил на каждом участке.
Тогда получаем:
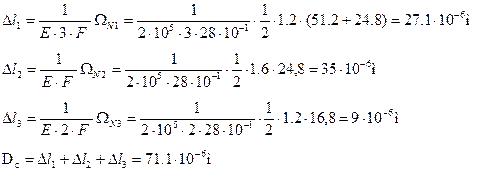
Стержень удлиняется.
Определим величины осевых перемещений характерных сечений.
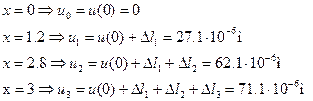
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.
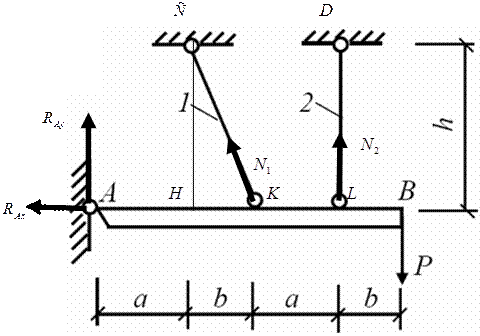
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F2/F1 и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:
1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γf = 1,2.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F2/F1. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γс = 0,9.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней, приняв Е=2,1·105 МПа.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
Таблица 2
| a, м | b, м | h, м | F2/F1 | Р, кН |
| 1,4 | 0,8 | 1,3 | 1,3 |
 1. Определим расчетные значения нагрузки:
1. Определим расчетные значения нагрузки:

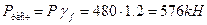
2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:
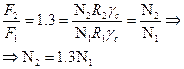
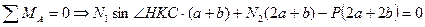 , где
, где
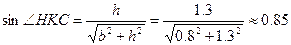
Тогда получаем:
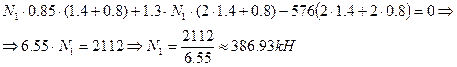
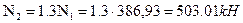
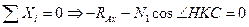 , где
, где 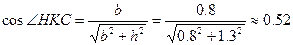
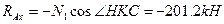
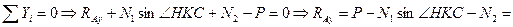 -256kH
-256kH
Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.
Вычисляем напряжения в стержнях 1 и 2
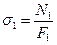 ,
, 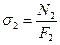
Определяем требуемые по условию прочности площади поперечных сечений
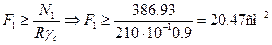
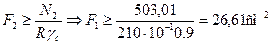
Проверим соотношение 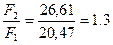 , условие выполняется.
, условие выполняется.
Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.
Стержень 1: профиль №7, 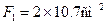 ,
, 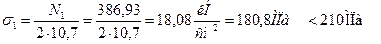
Стержень 2: профиль №10, 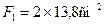 ,
, 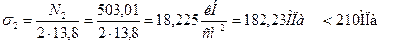
Определим удлинения стержней при 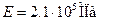
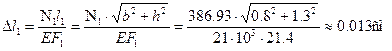
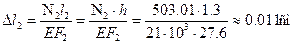
Определим нагрузку 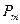
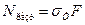 , σт = 240 МПа
, σт = 240 МПа
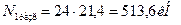
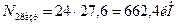
Находим из уравнения равновесия величину Рразр:
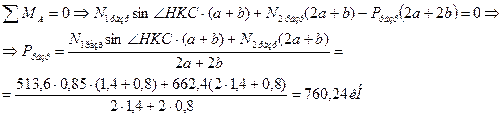
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.
Определяем величины опорных реакций.
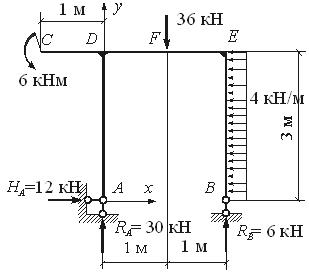
| SX = 0, | – 4·3 + HА = 0, | HА = 12 кН; | |
| SMА = 0 | 6 – 36·1 + 4·3·1,5 + 2RВ = 0, | RВ = 6 кН; | |
| SMВ = 0, | 6 + 36 + 4·3·1,5 – 2RА = 0, | RА = 30 кН; | |
| SU = 0 (проверка), | – 36 + 30 + 6= – 36 + 36 = 0. | ||
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
| Участок АD | ||
| Сечение А: | N = – RА = – 30 кН (сжатие), | Q = – HА= – 12 кН, M = 0 |
| Сечение D: | N = – 30 кН, Q = – 12 кН, | M = – 12*3 = – 36 кНм |
| (растянуты левые волокна). | ||
| Участок ВЕ | ||
| Сечение В: | N = – RА = – 6 кН, | Q = 0, M = 0, |
| Сечение E: | N = – 6 кН, Q = 4·3 = 12 кН, | M = – 4·3·1,5 = – 18 кНм |
| (растянуты правые волокна). | ||
| Участок CE | ||
| Сечение C: | N = 0, Q = 0, | M = – 6 кНм |
| (растянуты верхние волокна). | ||
| Сечение D (слева): | N = 0, Q = 0, | M = – 6 кНм. |
| Сечение D (справа): | N = – HА = – 12 кН, Q = RА = 30 кН, | M = – 6 – 12·3= – 42 кНм |
| Сечение F (слева): | N = – 12 кН, Q = 30 кН, | M= –42+30·1= – 12 кНм. |
| Сечение F (справа): | N = – 12 кН, Q = 30 – 36 = – 6 кН, | M = – 12 кНм. |
| Сечение Е: | N = – 12 кН, Q = – RВ = – 6 кН, | M = – 18 кНм. |
Построим эпюры N, Q, и M:
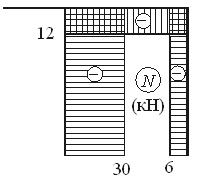
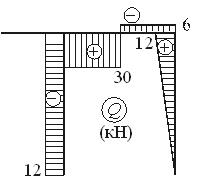
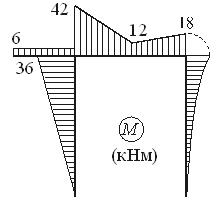
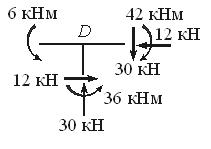
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:
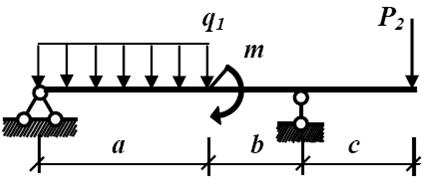
Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.
Материал балки сталь ВСт 3. Предел текучести σт = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге Rs = 130 МПа. Коэффициент условий работы γс = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γf = 1,2.
1.Определить опорные реакции;
2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.
3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.
Решение.
1. Определим опорные реакции.
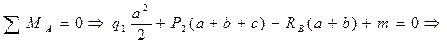
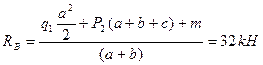
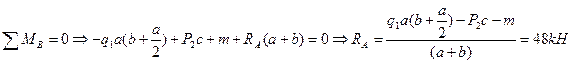
2. Проверка: 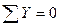 , получаем
, получаем
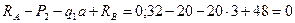
Реакции найдены правильно.
3. Построим эпюры Q и M.
Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.
Для эпюры Q:
I участок: 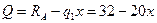
II участок: 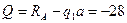
III участок: 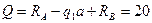 ,
,
В конце балки 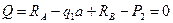
Для эпюры M:
I участок: 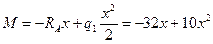 ; где
; где 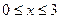
II участок: 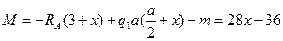 , где
, где 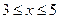 ;
;
III участок: 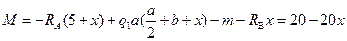 , где
, где 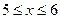 ;
;
На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.
Построим схему конструкции и эпюры Q и M:
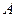
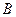
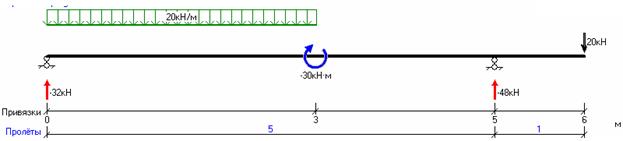
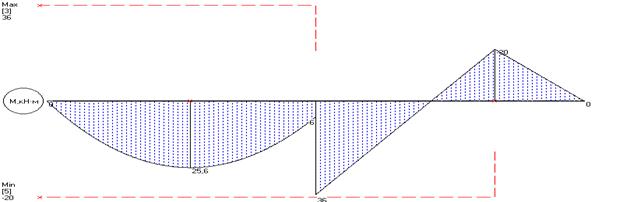
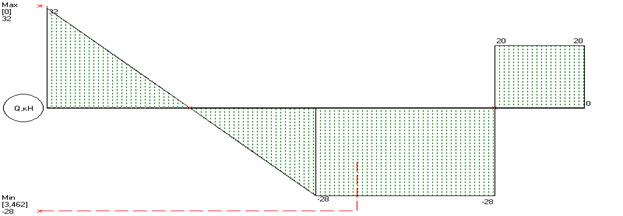
Значения М и Q в характерных сечениях балки указаны на эпюрах.
Опасным является сечение в точке с координатой 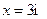 , где
, где 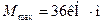 . Расчетное значение
. Расчетное значение 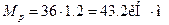
Требуемый момент сопротивления равен
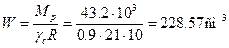
По сортаменту прокатной стали принимаем двутавровый профиль № 22
h=220мм, b=110мм, d=5.4мм, t=8.7мм, Jx=2550см4, W=232см3, Sx=131см3
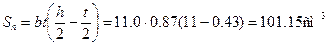
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:
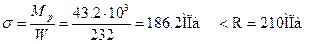
Прочность балки обеспечена.
6. Задания для контрольной работы
ЗАДАЧА № 1
Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:
1) положение центра тяжести;
2) положение главных центральных осей инерции и величины главных моментов инерции.
Таблица 2
| Первая буква фамилии студента | а, см | |
| А | П | |
| Б | Р | |
| В | С | |
| Г | Т | |
| Д | У | |
| Е | Ф | |
| Ж | Х | |
| З | Ц | |
| И | Ч | |
| К | Ш | |
| Л | Щ | |
| М | Э | |
| Н | Ю | |
| О | Я |
Схемы сечений стержней:
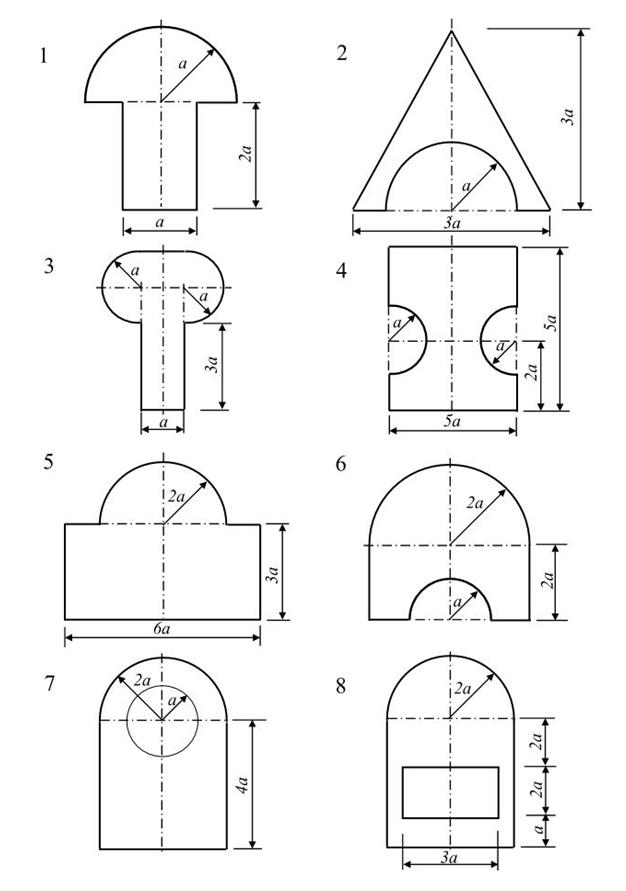
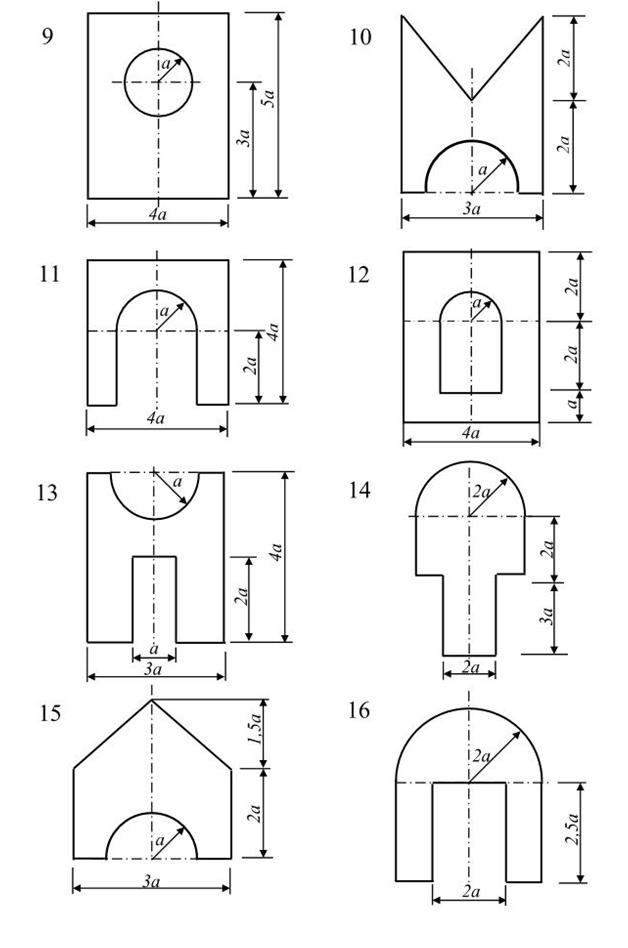
ЗАДАЧА № 2
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:
1) определить положение центра тяжести;
2) вычислить осевые и центробежные моменты инерции относительно центральных осей;
3) определить положение главных центральных осей инерции и величины главных моментов инерции;
4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;
5) сравнить результаты аналитического и графического расчетов.
Таблица 3
| Первая буква фамилии студента | Номер двутавра | Номер швеллера | Равнобокий уголок, мм | Неравнобокий уголок, мм | Лист, мм | |
| А | П | 80х80х6 | 100х63х8 | 160х10 | ||
| Б | Р | 90х90х6 | 110х70х8 | 160х12 | ||
| В | С | 90х90х8 | 125х80х7 | 180х10 | ||
| Г | Т | 100х100х8 | 125х80х8 | 180х12 | ||
| Д | У | 100х100х12 | 125х80х10 | 200х10 | ||
| Е | Ф | 110х110х7 | 140х90х8 | 200х12 | ||
| Ж | Х | 110х110х8 | 140х90х10 | 200х16 | ||
| З | Ц | 125х125х8 | 160х100х10 | 220х12 | ||
| И | Ч | 125х125х10 | 180х110х10 | 220х14 | ||
| К | Ш | 140х140х12 | 180х110х12 | 240х16 | ||
| Л | Щ | 160х160х12 | 200х125х14 | 240х20 | ||
| М | Э | 160х160х16 | 200х125х16 | 300х16 | ||
| Н | Ю | 200х200х16 | 250х160х12 | 350х16 | ||
| О | Я | 220х220х16 | 250х160х16 | 400х20 |
Схемы сечений стержней:


Date: 2016-02-19; view: 3963; Нарушение авторских прав