Критерії оптимальності та обмеження в задачах оптимального керування об’єктами

Реалізація оптимального керування об’єктами передбачає пошук та підтримання найкращого (оптимального) в певному смислі режиму функціонування. Задача оптимізації доповнює традиційні контури стабілізації, програмного та логіко-програмного керування.Для оцінки ефективності функціонування об’єкта використовують узагальнену кількісну оцінку, яка характеризує якість, ефективність керування, що дає можливість не лише виконати порівняльну оцінку різних режимів роботи об’кта, а й обрати найкращу. Така оцінка називається критерієм оптимальності, в загальному випадку - це функціонал, який дає можливість отримати інтегральну оцінку на певному інтервалі роботи (4.1).

Глобальний критерій оптимальності має природу прибутку:

(4.5)

де: – випуск певного виду продукції та її ціна; - сумарні затрати на виробництво продукції, які включають вартість сировини, енергії, матеріалів та ін. Кількісна оцінка, яку отримують з виразу (4.5), залежить від технологічного режиму і відповідності його розрахунковому, оптимальному, що забезпечується відповідною системою автоматизації. Критерій оптимальності (4.5) характеризує виробництво в цілому, в якому можна виділити стадії (підсистеми), на яких формується ціна продукції. Розв’язком задачі оптимізації за критерієм (4.5) є вектор технологічних змінних, які характеризують технологічний режим. Ці значення можуть бути завданням для локальних контурів регулювання технологічних змінних.

В загальній постановці задачі синтезу оптимального керування необхідно знайти мінімум функціоналу:

- для детермінованих систем:

(4.6)

- для стохастичних систем

(4,7)

де - функція, яка характеризує якість в кінцевий момент часу ; - сереждє значення функціоналу. М – оператор математичного сподівання.

Отже, критеріями оптимальності можуть бути як технічні, так і економічні узагальнені показники функціонування об’єкта або системи в цілому. При цьому одні показники повинні сягати максимуму (наприклад, продуктивність), інші – мінімуму (наприклад, витрати енергії).

Вибір критерія оптимальності - складна науково-технічна задача. Від вибору критерія залежать кінцеві результати функціонування об’єкта і системи, а сам процес вибору не піддається формалізації.

В задачах синтезу та аналізу АСР використовуються такі критерії оптимальності:

- мінімальної тривалості перехідного процесу (максимальної швидкодії):

­­­­­­­­­­­­ (4.8)

- мінімального відхилення регульованої координати:

(4.9)

(4.10)

Для обєкта з регульваними координатами

(4.11)

де: 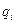- вагові коефіцієнти;

- мінімум витрати енергії

(4.12)

де: - вагові коефіцієнти; - керування;

- мінімум витрати матеріальних ресурсів – палива, сировини, каталізатора

(4.13)

або:

(4.14)

- досягнення кінцевого стану координати Х або об’єкта в цілому (термінальна задача)

(4.15)

Якщо об’єкт функціонує в умовах випадкових збурень, то якість окремого процесу буде гіршою, ніж в середньому за множиною процесів. В таких випадках використовуються середні значення показників:

- мінімізація похибки керування

(4.16)

- ймовірність помилки спостерігача (задача ідеального спостерігача)

(4.17)

де: - відповідно ймовірність помилкового виявлення сигналу, та його витрати;

- середнього ризику:

(4.18)

де: А - оператор системи, який зв’язує та ; - функція витрат (час процесу, витрати палива, та ін.);

- мінімальний критерій, який характеризує найкращий результат в найгірших можливих умовах:

(4.19)

В цьому випадку необхідно знайти максимальну оцінку з усіх можливих значень, для , що відповідає умовному ризику. , а мінімізується його максимальне значення. Для іншого завдання, яке характеризується вектором , будуть більші витрати, але у самому несприятливому випадку функція витрат буде меншою, ніж при мінімізації середнього ризику.

Для складних систем керування достатньо повно охарактеризувати процес функціонування за допомогою одного критерія оптимальності неможливо. Для цього випадку формується вектор критеріїв

(4.20)

що відповідає задачі векторної (багатокритеріальної) оптимізації. Такі задачі складні, розв’язуються як правило, шляхом багатоетапних оцінок, які мають суб’єктивний та еврістичний характер. Розв’язання задач векторної оптимізації можливе двома шляхами:

- зведення до задачі скалярної (однокритеріальної) оптимізації, коли обирається один головний критерій, а решта розглядається як обмеження, наприклад мінімізується критерій середньоквадратичного відхилення при обмеженнях на витрату енергії;

- формується згортка критеріїв за певними правилами (їх агрегування).

На перший погляд можливість оцінки рішень за кількома різними критеріями здається нереальною, однак на практиці саме такі задачі виникають найбільш часто, коли необхідно враховувати різні сторони функціонування об’єктів або систем, наприклад:

- робота кількох взаємозв’язаних апаратів, ефективність функціонування кожного з них оцінюється своїм критерієм;

- робота окремого апарата в різних умовах, наприклад при різній сировині, коли кожний режим оцінюється своїм критерієм.

Якщо визначено вектор координат задачі оптимізації Х, який належить множині (Х є ), а векторні критерії залежать від цього вектора, то необхідно знайти правило порівняння критеріїв. Це може бути саме згортка критеріїв, тобто скалярна функція від вектора , яка дає можливість визначити оптимальне значення Х. З множини допустимих розв’язків Д виділяють робочу підмножину , яка об’єднує розв’язки, отримані з розумного способу згортки критеріїв. Розумним способом згортки критеріїв називають такий, коли вектор , вважають кращим, ніж вектор , якщо всі компоненти цих векторів, крім і-го співпадають, а . Змінювання однієї складової робочої підмножини обов’язково приводить до певного погіршення інших, тому підмножина називається областю компромісів. 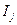Таким чином, множині компромісних рішень відповідає частина простору критеріїв, для якої неможливо покращити , не погіршуючи і навпаки. Такі задачі утворюють окремий клас Паретооптимальних задач (вперше в кінці ХІХ століття такі задачі сформулював італійський вчений – економіст В.Парето).Ідеальним буде той випадок, коли в результаті розв’язання задачі оптимізації можна отримати такі оптимальні керування, за яких кожний частинний критерій має мінімум (максимум). В той же час кожний частинний критерій віділяє „свою” множину оптимальних керувань, тому необхідно враховувати важливість кожного з критеріїв.В деяких задачах векторної оптимізації частинні критерії можна впорядкувати (ранжувати) за значимістю так, що необхідно добиватись приросту найбільш важливого критерія за рахунок втрат по інших критеріях.

В багатокритеріальних задачах оптимізації можна отримати кілька векторів керувань , і тоді виникає проблема порівняння їх ефективності. В детермінованих задачах приймається, що вектор керування , не гірший вектора в смислі векторного критерія, тобто , якщо виконуються нерівності

(4.21)

Якщо в (4.21) мають місце лише рівності, або керування і еквівалентні () щодо векторного критерія. Керування явно краще, має перевагу перед ,тобто , якщо мають місце нерівності (4.21), при чому хоча б одна з них виконується строго.

Нарешті, керування називають ефективним, якщо не існує кращого , тобто ефективними називають керування, які не можна покращити за векторним критерієм. Тоді оптимальним за векторним критерієм будуть ефективні керування .

Всі точки множини Парето можна отримати, розв’язуючи сімейство додаткових оптимізаційних задач:

(4.21)

де: - вектор пріоритетів.

Важливість частичних критеріїв визначають за допоміжними схемами:

- справедливий компроміс. За рахунок прийняття значень згортка (4.21) має чітко фіксовані пріоритети. При цьому відносне зниження одного або кількох критеріїв не перевищує відносного підвищення інших критеріїв.

В точці оптимума сумма відносних змін всіх критеріїв дорівнює нулю:

(4.22)

Цій умові відповідає згортка критеріїв

(4.23)

або

(4.24)

Одиниці вимірювань критеріїв не впливають на результат, тому що розраховуються відносні величини;

- послідовні поступки, без жорсткого пріоритету.

При такій схемі всі частинні критерії розташовуються та нумеруються в порядку їх відносної значущості. Забезпечується екстремум (мінімум або максимум) найбільш важливого критерія . Далі призначається величина зниження першого критерія і знаходять екстремум другого по значущості критерія за умови, що для значення першого критерія не повинно відрізнятись більше, ніж встановлена похибка:

(4.25)

Далі призначають поступку для другого критерія та знаходять екстремум третього кретерія з урахуванням поступок для першого та другого і т.д. Оптимальним є таке керування , яке забезпечує екстремум останнього за значущістю частинного критерія з урахуванням поступок для всіх інших критеріїв

(4.25)

- жорсткий пріоритет (ранжування частинних критеріїв) спочатку розв’язують однокритеріальну задачу з найбільш важливим критерієм . Якщо розв’язок не єдиний, то це значення фіксується як умова, за яким розв’язують задачу для другого критерія і т.д. Кількість умов в кожній наступній задачі оптимізації зростає, звужуючи множину її допустимих розв’язків. Якщо розв’язок для даного критерія єдиний, то розв’язки для інших задач втрачають смисл.

В реальних задачах математичні моделі задачі оптимізації та її умови визначені наближено, тому немає сенсу добиватись точного оптимуму 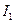та можна вважати допустимими задачі про оптимум всі ті значення Х, для яких зменшення 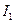в порівнянні з його граничним значенням не перевищує деякої величини , яка тим більша,чим більша похибка вихідних даних, тобто при розв’язанні задачі на оптимум до її умов додають обмеження

(4.26)

- метод „ідеалу”.

Рис.4.2. Площина критеріїв оптимальності

В просторі критеріїв або на площині (рис.4.2.) можна виділити т.А координати якої визначаються граничним значенням кожного з критеріїв , знайдених без урахування інших. Оптимальним вважається такий розв’язок, який знаходиться найближче до „ідеалу” по відстані, яка вимірюється в просторі критеріїв і є допустимим.

В наведених схемах компромісу розв’язок багатокритеріальної задачі зводиться до однокритеріальної або до багаторазового розв’язання задачі з одним критерієм.

Як вже зазначалось, задачі оптимізації розв’язуються в умовах обмежень та кординати стану, вихідні змінні та ресурси Обмеження в задачах оптимізації можуть бути природніми (об’єктивно існуючими) та штучними, які вводяться спеціально для конкретної задачі. До природніх обмежень відносяться такі, які існують у відповідності до фізичних законів, які визначають природу та закономірність функціонування об’єктів та системи в цілому. При формалізації задачі оптимізації, тобто подання її в математичний формі, обмеження визначаються математичними моделями об’єктів, якими і визначаються реальні значення змінних 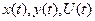. Зокрема до природніх обмежень відносяться: кількість обертів асинхронного двигуна, яка не може перевищувати синхронної; витрата речовини, яка визначається конструктивними розмірами трубопроводів і швидкістю течії та ін. До умовних обмежень відносяться штучно встановлювані допустимі значення, наприклад, координат стану (рис 4.3.)

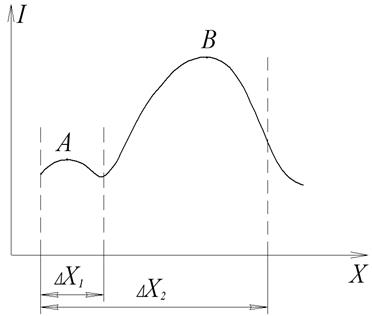
Рис 4.3. Залежність значення критерія від обмежень

Ці значення визначаються різними причинами: запобігання аварійних ситуацій, необхідність точного підтримання бажаного технологічного режима і т.д. Обмеження в задачах оптимізації відіграють важливу роль і визначають можливість досягнення бажаного результату. На рис 4.3. показана залежність критерія від координати Х, а також екстремальних значень від діапазонів обмежень та . Видно, що в умовах жорстких обмежень можливе досягнення лише локального екстремуму (т.А), а при збільшенні діапазона обмежень до можна отримати глобальний екстремум (т.В).

Таким чином, формалізація задачі оптимізації передбачає запис в математичній формі таких складових:

- критерій:

- математичні моделі, обмеження:

(4.27)

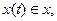
або

або або

В залежності від типу задачі оптимазації її розв’язком може бути вектор змінних оптимального технологічного режиму або вектор оптимальних керувань , або значення параметрів окремих елементів (наприклад, параметрів настройок автоматичних регуляторів) та ін.

Date: 2016-02-19; view: 1094; Нарушение авторских прав