Стійкість та якість імпульсних систем

За динамічними властивостями імпульсні системи з АІМ багато в чому аналогічні неперервним системам, що дає можливість застосовувати аналоги методів дослідження неперервних систем. Імпульсна система буде стійкою, коли вільна складова перехідного процесу Х_В(іТ_п) з часом затухає, тобто:

(3.32)

Ця складова є розв’язком однорідного різницевого рівняння:

(3.33)

Якщо однакових коренів z немає, то розв’язок рівняння (3.33) буде сумою:

(3.34)

При 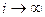розв’язок Х_В(іТ_п) прямує до нуля лише тоді, коли всі корені Z_k за модулем менші одиниці

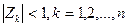(3.35)

Таким чином, загальною умовою стійкості імпульсних систем буде вимога знаходження коренів характеристичного рівняння всередині кола одиничного радіуса з центром в початку координат (рис.3.9,а).

Рис.3.9. Області стійкості імпульсних систем

При розташуванні хоча б одного кореня на самому колі система знаходиться на межі стійкості, при система нестійка. Отже, одиничне коло відіграє таку ж роль, як уявна вісь для неперервних систем (рис.3.9,б).

Для дослідження стійкості імпульсних систем можна використовувати алгебраїчні та частотні критерії стійкості. Для застосування критерія Рауса – Гурвиця в характеристичному рівнянні замінюють змінну Z на змінну підстановкою:

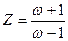(3.36)

і отримують перетворене характеристичне рівняння:

(3.37)

Кореням рівняння (3.33), розташованим в одиничному колі, будуть відповідати корені рівняння (3.37) (рис.3.9,в), які знаходяться зліва від уявної осі. Це можливо, коли 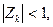тобто вектор знаходиться в лівій на півплощині.

При використанні критерія Михайлова в характеристичний поліном підставляють і при змінюванні частоти від 0 до будують годограф вектора (рис.3.10,а). Імпульсна система буде стійкою, коли годограф повернеться проти годинникової стрілки на кут . На рис.3.10,а: 1 – стійка система; 2 – нестійка; 3 – на межі стійкості. Необхідно врахувати, що імпульсні системи другого і навіть першого порядків на відміну від неперервних можуть бути нестійкими при додатніх коефіцієнтах характеристичного рівняння. Це пояснюється тим, що фіксатор вносить додаткове запізнювання.

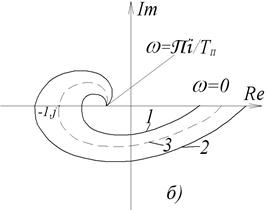
Рис.3.10. Визначення стійкості імпульсної системи

Критерій Найквіста для імпульсних систем формулюється так же, як і для неперервних: система стійка, якщо годограф 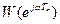стійкого розімкненого контура не охоплює точку (-1; j₀). Стійкість розімкненого контура визначається стійкістю неперервної частини: якщо вона стійка, то буде стійкою і замкнена система з імпульсним елементом. На рис.3.10,б: 1 – стійка система; 2 – нестійка; 3 – на межі стійкості.

Імпульсний елемент не впливає на стійкість розімкненого контуру, але для замкненої системи необхідно врахувати таке:

- при малих періодах повторення T_n частотна характеристика розімкненого контура співпадає з частотною характеристикою неперервної частини, яка визначає стійкість імпульсної системи;

- при збільшенні періоду повторення в більшості систем зменшується граничний передаточний коефіцієнт, погіршуються динамічні властивості;

- в окремих випадках (структурно-нестійкі неперервні системи, системи із запізнюванням) імпульсний елемент справляє стабілізуючу дію. Для таких систем рекомендується обирати період повторення T_n з умови:

(3.38)

де: - частота, при якій АФХ неперервної частини перетинає додатну уявну вісь.

Для оцінки якості імпульсних систем використовуються такі ж показники, як і для неперервних: точність в усталених режимах, тривалість перехідного процесу і інш.

Тривалість і перерегулювання оцінюють безпосередньо за перехідною характеристикою. Для її отримання записують Z – зображення вихідної величини при одиничному ступінчастому сигналі:

(3.39)

і за зображенням знаходять оригінал – решітчасту функцію 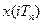. В простих випадках для цього достатньо таблиць оберненого Z – перетворення, розклавши попередньо зображення X(Z) на прості дроби.

В більш складних випадках розкладають функцію X(Z) в степеневий ряд за від’ємними степенями Z (діленням чисельника на знаменник):

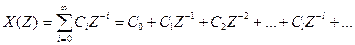(3.40)

З визначення Z – перетворення випливає, що коефіцієнти цього степеневого ряду є значеннями перехідної характеристики h(t) в дискретні моменти часу t=iT_n (I=0,1,2…), тобто:

С₀=Х(0); С₁=Х(Т_п); С₂=Х(2Е_п);... С_l=X( T_n) (3.41)

В імпульсних системах перехідні процеси можуть закінчуватись за кінцеве число періодів T_n, яке дорівнює порядку системи n. Умовою отримання кінцевої тривалості перехідного процесу є рівність всіх (крім першого) коефіцієнтів характеристичного рівняння нулю:

a_n-1 = a_n-2 =…= a₀ =0 (3.42)

Тоді характеристичний поліном має вид:

F(z)= a_nzⁿ, (3.43)

а зображення вихідної величини буде кінцевим рядом:

(3.44)

що відповідає перехідному процесу кінцевої тривалості t_n = nT_n. При іншому співвідношенні коефіцієнтів тривалість перехідного процесу більше nT_n. Саме процес кінцевої тривалості буде оптимальним за швидкодією. Для цього в реальні системи вводяться неперервні та імпульсні ланки корекції.

Точність імпульсної системи оцінюють за усталеним значенням сигналу похибки:

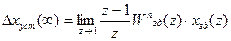(3.45)

При ступінчастому сигналі х_зд(t) = a1(t) усталена похибка буде:

(3.46)

Видно, що при ступінчастому сигналі похибка дорівнює нулю, якщо передаточна функція W_роз(z) має хоча б один полюс, який дорівнює одиниці. При лінійному сигналі для цього потрібно не менше 2-х полюсів.

Приклад. Побудувати перехідну характеристику системи, яка складається з “ключа”, фіксатора (3.6) та ідеальної інтегрувальної ланки.

Передаточна функція розімкненого контура:

(3.47)

Передаточна функція замкненої системи:

(3.48)

Вихідний сигнал при ступінчастій дії буде:

(3.49)

або, розклавши на два дроби:

(3.50)

За таблицями зворотного перетворення находимо:

(3.51)

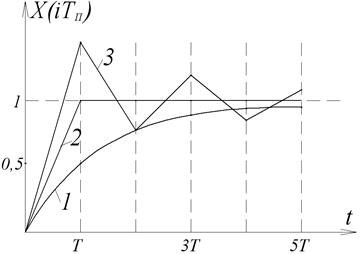
Рис.3.11. Перехідні процеси в імпульсній системі

На рис.3.11 показані перехідні процеси при kT_n = 0,5 (крива 1); kT_n = =1 (2); kT_n = 1,5 (3). Оптимальним буде перехідний процес 2.

Date: 2016-02-19; view: 488; Нарушение авторских прав