Синтез оптимальних систем

Для технологічних об’єктів найбільш важливими є системи, оптимальні за швидкодією та квадратичними критеріями. Задача розробки систем, оптимальних за швидкодією, виникає коли необхідно мінімізувати час перехідного процесу в таких режимах: пуск, зупинка, перехід з одного режиму на інший. Тоді критерій оптимальності записується так:

(4.54)

В лінійних системах швидкодія може бути як завгодно великою, що забезпечується введенням необхідних ланок та ланцюгів корекції. Наприклад, якщо перед аперіодичною ланкою включити ПД – ланку корекції, то можна компенсувати її інерційність і отримати нескінченно велику швидкодію, коли час перехідного процесу . Для системи -го порядку для отримання такого ж результату необхідно включити ланки корекції з похідними.

Для реальних нелінійних систем завжди існують обмеження на змінні та їх похідні, що обмежує швидкодію, повна компенсація інерційності за рахунок похідних не реалізується, тому при стрибкоподібному змінюванні вхідного сигналу похідна буде нескінченно великою, що не пропускається ланкою внаслідок обмеження статичної характеристики. Наприклад, для електричного двигуна постійного струму вихідною змінною є кількість обертів, вхідною напруга якоря. В зв’язку з обмеження цієї напруги за умови електричної міцності та механічної цілісності якоря при дії центробіжних сил час перехідного процесу (зміни кількості обертів від одного значення до іншого) буде мати кінцеве значення.

Для системи першого порядку, яка подана у вигляді аперіодичної ланки (рис.4.7, а), необхідно забезпечити можливу швидкодію в умовах обмеження вхідного сигналу при змінюванні від 0 до (статичного значення). Очевидно, спочатку сигнал необхідно змінити від 0 до максимального значення 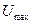і утримувати його таким до того часу, поки не досягн значення .

Рис.4.7. Перехідні процеси в системі 1-го порядку

Після цього значення необхідно миттєво змінити до величини:

(4.55)

де: - коефіцієнт передачі, який відповідає статичній характеристиці.

Тривалість перехідного процесу (рис.4.7,б) визначається інерційною ланкою (постійною часу Т, величиною 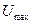та значенням на початку та в кінці перехідного процесу). Якщо ,то , що відповідає випадку компенсації інерційності лінійної ланки за допомогою додаткового діяння за похідною.

Рис.4.8. Перехідні процеси в системі 2-го порядку

Для систем 2-го порядку (рис.4.8) необхідно враховувати обмежене значення при обмеженому :

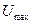(4.56)

На початку сигнал необхідно стрибкоподібно змінювати так, як це розглядалось в попередньому випадку для системи першого порядку (ділянка 1 на рис.4.8). коли змінна досягне максимального значення , необхідно миттєво змінити керування з до 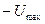і підтримувати його до моменту часу, коли не досягне значення (ділянка 2):

(4.57)

Таким чином, для системи 2-го порядка процес керування в задачі максимальної швидкодії включає два інтервали з граничними значеннями і .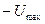

Для систем 3-го порядку оптимальний перехідний процес керування буде складатись з трьох інтервалів, на кожному з яких керування приймає одне з граничних значень із змінюванням знаку на межах інтервалу. При цьому знак на першому інтервалі співпадає зі знаком кінцевого стану , тому що сигнал на вході другої ланки повинен бути близьким до сигналу для системи 1-го порядка. В той же час, з урахуванням інерційності першої ланки сигнал на вході другої буде змінюватись не миттєво, а за експонентою.

В загальному випадку для послідовно з’єднаних лінійних ланок 1-го порядку з дійсними від’ємними коренями характеристичного поліному оптимальне керування при наявності обмежень на складається з інтервалів, на кожному з яких цей сигнал приймає граничне значення, тобто керування є релейним. В кінці кожного інтервалу змінюється знак , а на першому інтервалі знак визначається необхідним напрямком зміни вихідного сигналу . Ці висновки справедливі при нульових початкових умовах. Якщо початкові умови довільні, то кількість інтервалів може бути меншою, аж до одного. Дійсно, якщо в момент розгляду процесу керування стан об’єкта (значення 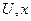та їх похідних) виявляється таким, як в кінці -го інтервалу оптимального керування, при переведенні об’єкта в той же заданий стан за інших початкових умов, то кількість інтервалів буде .

Ці міркування узгоджуються з тим принципом, згідно якого будь-який кінцевий відрізок оптимальної траекторії буде також оптимальним. Ці результати є наслідками теореми про інтервалів Фельдбаума А.А.

Теорема про інтервалів доводиться строго за допомогою принципа максимума Л.С. Понтрягіна.

Об’єкт описується системою рівнянь:

(4.58)

або у векторній формі

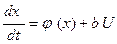(4.59)

Приймається обмеження у формі:

(4.60)

де: - граничне значення керування.

Запишемо для системи гамільтоніан

(4.61)

де: . Від сигналу керування залежить лише другий доданок, тому максимум з урахуваннями (4.61) буде при:

(4.62)

Цей вираз показує, що керування весь час буде мати граничне значення , тобто релейний закон оптимального за швидкодією керування справедливий для нелінійного об’єкта, який описується рівняннями (4.59).

Для лінійного об’єкта рівняння (4.58) набуває виду:

(4.63)

Спряжені рівняння будуть:

(4.64)

а

(4.65)

Якщо характеристичне рівняння об’єкта, який описується диференціальними рівняннми (4.63) при , має всі корені дійсні, то це справедливо і для спряжених рівнянь (4.64). Це значить, що розв’язок цих рівнянь має вид суми експоненційних складових:

(4.66)

де: - дійсні числа; - постійні інтегрування. Тоді у відповідності до (4.62):

(4.67)

де:

Сума експонент в (4.67)може переходити через 0 не більше разів, тобто кількість інтервалі в з постійним знаком буде не більше , що й потрібно було довести.

До викладеного матеріалу необхідно додати таке:

- якщо обмеження накладено не лише на сигнал керування , а й на довільне число проміжних змінних рівняння об’єкта, то кількість інтервалів оптимального керування буде більшою;

- в цьому розділі розглядалась задача оптимальної швидкодії, при зміні завдання. Викладений матеріал справедливий також для перехідних процесів, які викликані збуреннями. В цьому випадку необхідно забезпечити найшвидше повернення об’єкта до початкового стану.

При синтезі замкненої системи керування додатково до принципу максимуму використовують метод фазових траекторій, за допомогою якого визначають рівняння поверхонь перемикання:

(4.65)

а також функції перемикання

(4.66)

які приймають нульові значення на поверхні перемикання.

Поверхня (лінія) перемикання у звязку з неперервною залежністю оптимальної траекторії від початкових умов являє собою неперервну, кусково-гладку поверхню (лінію), яка розділяє простір станів на дві області, які відповідають різним знакам сигналів керування. Форма і положення поверхні перемикання залежать як від виду і параметрів рівняння об’єкта, так і від виду і параметрів зовнішніх сигналів та . Якщо прийняти в якості змінних стану відхилення , то поверхня пермикання обов’язково пройде через початок координат, де закінчується перехідний процес, який починається в будь­-якому початковому стані 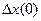. Якщо порядок зовнішнього діяння у вигляді степеневої функції менший порядку астатизму системи, то поверхня перемикання буде кососиметричною відносно початку координат.

Рис 4.9.Лінія перемикання для об’єкта другого порядку

Некососитетрична лінія перемикання АОВ для об’єкта другого порядка (рис 4.9.) розділяє фазову площину на дві області, які відповідають різним знакам сигналів керування . В залежності від початкових умов (початкового стану об’єкта) можуть бути різні варіанти керування, які переводять об’єкт в початок координат.

Якщо точка М₁ знаходиться над лінією перемикання, то керування спочатку бути від’ємним, а в точці М₂ - додатнім. Якщо точка N₁ розташована нижче лінії перемикання, то сигнал керування спочатку додатній, а точці N ₂- від’ємний. В частинному випадку, коли початкова точка знаходиться на лінії перемикання, (точки А або В), змінювати знак керування на протязі перехідного процесу не потрібно.

Знак сигналу керування на першому інтервалі визначається знаком функції перимикання 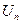в початковій точці. Функцію перемикання доцільно записувати так, щоб її знак з різних сторін лінії перемикання співпадав із знаком сигналу керування:

(4.70)

Таким чином, задача синтезу оптимальної за швидкодією замкненої системи зводиться до пошуку в просторі станів функції перемикання та її реалізації в пристрої керування. Ортимальне керування буде:

(4.71)

Це керування формується двохпозиційним пристроєм, вихідний сигнал якого приймає лише максимальні значення ; .

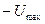Визначення рівнянь для поверхні перемикання і відповідної функції при наявності зовнішніх сигналів - завдання і збурення - є складною задачею. В цьому випадку ці сигнали необхідно враховувати в рівнянні об’єкта або вимірювати і вводити в обчислювальний критерій, який реалізує функцію перимикання, але поверхня перемикання дрейфує в ­просторі станів. Викладений підхід порівняно просто реалізується лише для об’єктів не вище другого порядку, коли зовнішні сигнали є степеневими функціями, порядок яких не перевищує порядок об’єкта.

Синтез замкнених лінійних систем керування розроблено російським вченим О.М.Лєтовим і американцем Р.Калманом. Ці процедури назвали методикою аналітичного конструювання оптимальних регуляторів (АКОР). В цій задачі використовується узагальнений квадратичний критерій якості функціонування:

(4.72)

де: - вектор сигналів похибок;

q - діагональна невід’ємно визначена матриця вагових коефіцієнтів, які оцінюють степінь небажаності відхилень вихідних змінних від заданих значень; r- діагональна позитивно визначена матриця коефіцієнтів, які відповідають вартості енергії окремих керувань.

Якщо розглядається об’єкт, змінні стану якого піддаються повному і точному спостереженню, то для нього записується матричне диференціальне рівняння (за умови стаціонарності):

(4.73)

та алгебраїчне рівняння виходу

(4.74)

Нагадаємо ще раз позначення змінних і констант в рівняннях (4.73) - (4.74):

- вимірний вектор стану з компонентами ;

-вимірний вектор керувань;

- вимірний вектор збурень типу „білий шум” з інтенсивностями ;

- вимірний вектор вихідних змінних,які повинні відповідати певним вимогам;

- постійні матриці, елементи яких є параметрами об’єкта.

В першому наближенні приймається, що керування не обмежені, і щодо розмірностей векторів виконується співвідношення:

(4.75)

В задачах стабілізації вихідних змінних забезпечується мінімум середньоквадратичного відхилення , що відповідає та мінімуму середньоквадратичного відхилення керування . Тоді мінімізується квадратичний функціонал:

(4.76)

Діагональні матриці враховують „штрафи” за відхилення та векторів . Вагові коефіцієнти підбирають експериментально шляхом послідовних ітерацій з визначення результатів на основі моделювання. При цьому головною закономірністю є: чим більше значення коефіцієнтів , тим ширша смуга пропускання замкненої системи,тобто збільшується швидкодія, чим більші значення коефіцієнтів , тим більша інерційність системи.

Задача стабілізації вихідних змінних за критерієм (4.76) еквівалентна задачі стабілізації змінних стану за критерієм (4.77)

де:

Головним висновком, який отримали А.М.Лєтов і Р. Каллман, є:

- для системи керування,яка функціонує в режимі стабілізації оптимальні керування , які відповідають мінімуму функціоналів (4.76) або (4.77), є лінійними функціями змінних стану:

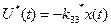(4.78)

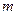де: -матриця коефіцієнтів зворотніх зв’язків між змінними стану та керуваннями,

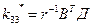(4.79)

Матриця Д є симетричною позитивно-визначеною розміром і знаходиться як розв’язок нелінійного матричного алгебраїчного рівняння Ріккаті.

(4.80)

Оптимальні коефіцієнти зворотніх зв’язків в задачах стабілізації не залежать від параметрів випадкового збурення типу „білий шум”, але від цих параметрів залежить мінімально-досяжне значення критерію (4.77). Так, якщо - векторний „білий шум”, то мінімальне значення критерія буде:

(4.81)

де:

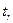- слід матриці (сума діагональних елементів);

-матриця інтенсивностей компонент вектора розміром .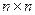

Для системи стабілізації існує оптимальна передаточна функція, яка зв’язує вихід та задане значення :

(4.82)

При керуванні складними об’єктами, математичні моделі яких мають довільний порядок оператор оптимального керування буде також складним з використанням похідної змінної -го порядку.

Це приводить до труднощів реалізації таких систем, тому використовують квазіоптимальні системи (близькі до оптимальних). Такий підхід передбачає два можливих шляхи реалізації:

- спрощення знайденого строго оптимального оператора;

- синтез оптимального оператора для попередньо спрощеного об’єкта.

[1, с.71-96, 2, с.462-498]

Контрольні запитання.

1. Дайте визначення поняття „оптимізація”.

2. Що називають критерієм оптимальності?

3. В якому вигляді отримують оптимальне керування?

4. Наведіть класичну постановку задачі оптимального керування.

5. Наведіть класифікацію задач оптимізації стосовно систем керувань.

6. Які методи оптимізації використовуються при синтезі оптимальних систем керування?

7. Наведіть приклади критеріїв оптимальності для детермінованих та стохастичних систем.

8. Коли виникають задачі векторної оптимізації?

9. Що таке згортка критеріїв та область компромісів?

10. Як оцінюється важливість частинних критеріїв оптимальності?

11. Яка природа обмежень в задачах оптимізації?

12. Як формалізуються задачі оптимізації системи керування?

13. Наведіть суть принципу максимуму Л.С.Понтрягіна.

14. Які процедури використовуються при використанні принципу максимуму?

15. Наведіть геометричну інтерпретацію принципу максимуму.

16. Як формулюється задача оптимізації при використанні методу динамічного програмування?

17. Наведіть приклад застосування методу динамічного програмування для оптимізації багатостадійного процесу.

18. Наведіть приклад функції Беллмана.

19. Наведіть приклад системи, оптимальною за швидкодією 1-го, 2-го та n-го порядків.

20. Як формулюється і які наслідки має теорема про n інтервалів.

21. Як використовується принцип максимуму при розв’язанні задачі на максимальну швидкодію.

22. Як формулюється задача аналітичного конструювання оптимальних регуляторів?

Date: 2016-02-19; view: 472; Нарушение авторских прав