Лінійні диференціальні рівняння АСР

В загальному випадку динамічні властивості одноконтурної АСР описуються диференціальним рівнянням виду:

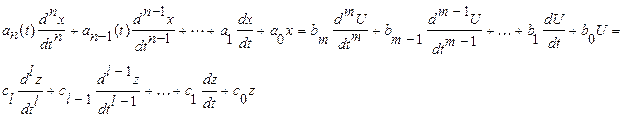
де: X,U,z – координати стану (регульована координата) та вхідні змінні – керуюча дія та збурення, - коефіцієнти;

В рівнянні (2.11) необхідно врахувати фактор часу, тобто фактично всі змінні залежать від часу – x(t),U(t),z(t). Коефіцієнти диференціального рівняння називають параметрами, значення яких визначаються особливостями об’єкта: конструктивними і режимними, наприклад швидкістю протікання процесів, константами тепло- та масообміну, хімічних реакцій. Якщо розглядаються нестаціонарні системи, то коефіцієнти диференціального рівняння залежать від часу -.

Зручною формою запису рівняння (2.11) є операторна, або символічна. Для цього вводиться оператор

. (2.12)

З урахуванням (2.12) диференціальне рівняння (2.11) в операторному вигляді має вид:

(2.13)

або:

, (2.14)

де: - власний оператор; , - оператори діянь.

Лінійні диференціальні рівняння першого, другого, а часом і більш високих порядків записують в стандартній (канонічній) формі, коли вихідна координата та її похідні знаходяться в лівій частині рівняння, вхідні змінні – в правій частині, а коефіцієнт при Х дорівнює одиниці. Наприклад, диференціальне рівняння першого порядку (n=1) має вид:

, (2.15)

Для приведення до стандартної форми поділимо вираз (2.15) на , тоді

, (2.16)

де: - постійна часу; ; - коефіцієнти передачі відповідно за керуючою дією та збуренням.

Стандартна форма диференційного рівняння дозволяє оцінити деякі важливі показники елемента чи системи: постійна часу T завжди має розмірність часу (с, хв) і визначає інерційність системи, наприклад тривалість перехідного процесу t_n=(3 4)T. Коефіцієнти передачі також мають важливий фізичний зміст: вони показують, наскільки змінилась вихідна величина при зміні вхідної на одиницю. Наприклад, оцінюється змінювання температури при зміні подачі пари, тоді розмірність коефіцієнта передачі буде . Часто керуючу дію оцінюють в одиницях переміщення регулюючого органу, його коефіцієнт передачі має розмірність (хРО – хід регулюючого органу).

Диференціальне рівняння (2.11) описує поведінку системи в динаміці, його розв’язком є перехідні процеси при різних вхідних діяннях та заданих початкових умовах:

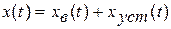, (2.17)

де: - вільна складова, в стійких системах з часом зникає, це перехідна складова;

- змушена, усталена складова, це те значення, до якого прямує x(t) при t→ .

Розв’язок диференціальних рівнянь знаходять, виконуючи такі етапи: знаходження загального розв’язку однорідного рівняння, частинного неоднорідного, загального та власне розв’язку з числовими значеннями постійних коефіцієнтів. Вільна складова – це розв’язок оператора (рівняння 2.13) і він має n складових (n – порядок системи):

, (2.18)

де: - постійні інтегрування; - корені полінома .

З диференціальних рівнянь можна отримати також рівняння статики, прирівнявши похідні нулю (p=0). Для рівняння (2.15) статична характеристика буде

, (2.19)

Передаточні функції. В теорії автоматичного керування зручною і найбільш наочною формою визначення закономірностей перетворення вхідних сигналів є предаточна функція. В операторному вигляді – це відношення оператора дії до власного оператора, причому кількість передаточних функцій дорівнює кількості вхідних сигналів:

, (2.20)

, (2.21)

тобто (2.22)

Передаточні функції мають нулі (корені рівняння R(p)=0) і полюси (корені рівняння D(p)=0). На основі виразів (2.20)-(2.22) визначається фундаментальна залежність:

, (2.23)

Таким чином, передаточні функції мають чіткий фізичний зміст: показують як перетворюється вхідний сигнал (передається з входу на вихід). Передаточні функції зручно отримувати з диференціальних рівняннь в операторному вигляді, наприклад рівняння (2.16) можна записати так:

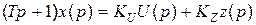, (2.24)

тоді

, (2.25)

Передаточні функції можуть бути також в формі зображень Лапласа:це відношення зображення вихідної величини до зображення вхідної за нульових початкових умов. Формально це можна отримати підстановкою в (2.20)-(2.22) р=s (s-комплексне число), але це справедливо лише для стаціонарних систем, тоді

, (2.26)

Частотні характеристики. При розв’язанні задач аналізу та синтезу необхідно оцінювати також властивості елементів та систем в частотній області, при різних частотах вхідних сигналів. Частотні характеристики – це реакція елемента чи системи на гармонійний сигнал (2.9) при змінюванні частоти від 0 до . Вихідний сигнал відрізняється від вхідного амплітудою та фазою:

, (2.27)

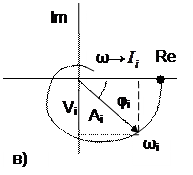
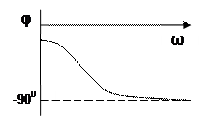
Динамічні властивості досліджуваних елементів чи систем визначаються амплітудно-частотною А(ω), фазо-частотною φ(ω) та амплітудно-фазовою характеристиками (рис.2.4).

		б)

Рис.2.4 Частотні характеристики,а - амплітудно-частотна (АЧХ); б - фазо-частотна (ФЧХ); в - амплітудно-фазова (АФХ)

При збільшенні ω амплітудно-фазова характеристика А(ω)→0, тобто проявляються інерційні властивості елемента та системи. Чим менша інерційність, тим ширша А(ω), тобто більша смуга (діапазон) пропускаємих частот. Часто існує резонансна частота, коли А(ωр) має максимальне значення.

Фазо-частотна характеристика φ(ω) від’ємна, тобто вихідні коливання відстають від вхідних за фазою.

На комплексній площі А(ω) та φ(ω) об’єднуються в одну - амплітудно-фазову характеристику (АФХ) – рис.2.4,в. Це крива (годограф), яку описує кінець вектора А при зміні частоти від 0 до . Проеції вектора на дійсну (Rе) та уявну (Im) осі – дійсна U(ω) та уявна V(ω) частотні характеристики.

Важливою особливістю лінійних систем є те, що частота вхідних та усталених вихідних (після зникнення перехідної складової) сигналів співпадають. Крім того, якщо розглядати відношення амплітуд вихідного та вхідного сигналів, то при ω=0 – це коефіцієнт передачі

(А(0)=К).

Частотну характеристику можна отримати підстановкою р=jω в вираз для передаточної функції, наприклад (2.20), тоді

, (2.28)

Цей вираз називають частотною передаточною функцією, яку можна подати у вигляді:

, (2.29)

де: , (2.30)

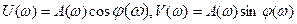(2.31)

В загальному випадку виконують такі перетворення: записують вираз:

, (2.32)

після чого звільняються від уявності в знаменнику:

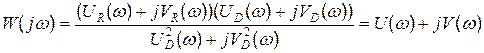, (2.33)

де: (2.34)

, (2.35)

В практичних розрахунках користуються також логарифмічними частотними характеристиками, побудованими в логарифмічних координатах, тому їх можна замінити ломаними лініями, складеними з кількох прямолінійних відрізків. Крім того, в логарифмічних координатах легко знаходити характеристики різних з’єднань елементів: операціям множення і ділення відповідають додавання та віднімання ординат логарифмічних характеристик, наприклад:

; , (2.36)

Амплітудно-фазові характеристики будуються в координатах , фазочастотні - . Одиницею довжини по осі частот є декада – інтервал частот між ω_і та 10ω_і. Ординати логарифмічної амплітудно-частотної характеристики вимірюють в логарифмічних одиницях – белах (Б) або децибелах (дБ), що відповідає відношенню потужностей двох сигналів: якщо потужність одного сигналу більша (або менша) іншого в 10 разів, тоді потужності відрізняються на 1Б (lg10=1). Потужність гармонійного сигналу пропорційна квадрату його амплітуди, тому при вімірюванні відношення амплітуд перед логарифмом необхідно враховувати множник 2. Наприклад, на деякій частоті А(ω) =100, що означає різницю вхідного і вихідного сигналів в 100² разів, тобто 2·lg100=4Б (40 дБ), а L(ω)=20·lgА(ω)=40 дБ.

За видом частотних характеристик всі елементи і системи поділяються на дві групи: мінімально-фазові і немінімально-фазові. Мінімально-фазовими називають такі елементи і системи, для яких всі нулі та полюси передаточної функції W(p) мають від’ємні дійсні частини та фазовий зсув φ(ω) є мінімальним в порівнянні з іншими елементами, які мають таку ж амплітудно-частотну характеристику А(ω), але хоча б один полюс чи нуль у них має додатню частину. Для мінімально-фазових елементів і систем достатньо знати А(ω), U(ω) i V(ω) для повної оцінки їх характерстик.

Часові характеристики. Це реакція елемента чи системи на типові вхідні сигнали – стрибкоподібний чи імпульсний (рис.2.5).

Часові функції є наочними, за їх видом можна оцінити загальні властивості елемента чи системи, які визначають їх динамічні особливості. З математичної точки зору часові характеристики є розв’язком диференціального рівняння, яке описує поведінку елемента чи системи в залежності від виду зовнішнього сигналу (це визначається правою частиною диференціального рівняння) та початкових умов, як правило нульових. Перехідна функція h(t) (рис.2.5,а) – зміна вихідної величини з часом при подачі на вхід одиничного ступінчатого сигналу за нульових початкових умов.

Рис.2.5. Часові характеристики: а) – перехідна функція h(t)

б) – імпульсна перехідна функція w(t)

Імпульна перехідна функція w(t) (рис.2.5,б) – зміна вихідної велечини з часом після подачі на вхід сигнала у вигляді -функції. Цю характеристику називають також ваговою функцією, або функцією ваги.

В задачах аналізу та синтезу використовуються різні динамічні характеристики, тому важливо знати і зв’язок між ними, який є однозначним тому, що фактично – це відображення одних і тих же властивостей елемента чи системи в різній формі. В той же час це дає можливість використовувати в конкретній задачі саме такі характеристики, які є найбільш зручними. Вище вже вказувалось, що перехідна функція h(t) – розв’язок диференціального рівняння. Враховуючи, що -функція і одиничний стрибок зв’язані між собою залежністю

, (2.37)

справедливі також залежності:

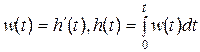, (2.38)

зображення за Лапласом одиничного стрибка

, (2.39)

тому , (2.40)

, (2.41)

де: - символ зворотнього перетворення Лапласа.

Date: 2016-02-19; view: 592; Нарушение авторских прав