Відносна діелектрична проникність

Речовина	Частота, Гц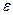
Повітря	0...3∙1010	1,000536
Вода		81,1
Вода	109
Вода	2,4∙1010
Парафін	106 - 109	2,2
Скло свинцеве	103 - 106	6,9
Поліетилен	106 - 109	2,3
Слюда	103 - 108
Титанат барію	106
Лід	І03 - 106

При аналізі виразу (7.10) з використанням даних табл. 7.1 можна зробити висновки про те, що швидкість поширення електромагнітних хвиль у різних середовищах може значно відрізнятись від швидкості світла .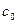

Частота та період хвилі. Ці поняття вводяться для гармонічних елект­ромагнітних хвиль, тобто хвиль, в яких напруженості електричного та магнітного полів змінюються за синусоїдним (косинусоїдним) законом. Нагадаємо, що синусоїда та косинусоїда відрізняються одна від одної тільки початком відліку. Як було зазначено в §7.1, хвиля - це процес, який залежить від двох змінних: координати та часу. Отже, у гармонічній електромагнітній хвилі закон зміни напруженостей електричного та магнітного полів визнача­ється функцією типу , де - кут, значення якого називають фазою.

Розглянемо більш докладно залежність фази гармонічної хвилі від часу 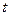та координати, наприклад 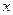. Як відомо, функція є періодичною, тобто з інтервалом для значення повторюються. Отже, у гармонічній електромагнітній хвилі величини напруженостей полів та будуть повто­рюватись через проміжок часу , за який фаза змінюється на . Цей проміжок часу називають періодом хвилі. Чим він менший, тим швидше змінюється фаза. Обернена періоду величина називається циклічною частотою. Вона показує швидкість зміни за часом напруженостей та і вимірюється в герцах (Гц). Якщо Гц, то це означає, що за одну секунду фаза змінюється на . Для довільної частоти /протягом секунди фаза зміни­ться на . Величина називається кутовою частотою, вимірюється вона в радіанах за секунду (рад/с).

Головною особливістю гармонічних функцій (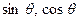) є те, що швидкість їх зміни (похідна) є також гармонічною величиною (). Як зазначено раніше, електричне поле електромагнітної хвилі породжується змінним за часом магнітним, а магнітне - електричним полями. Через згадану вище особливість гармонічних функцій, для гармонічних електромагнітних хвиль "автоматично" виконуються умови однаковості законів зміни електрич­ного та магнітного полів, тобто умова існування електромагнітної хвилі.

Хвильове число. Хвильовий характер електромагнітного поля відо­бражає загальну закономірність, відповідно до якої миттєве передавання взаємодії з однієї точки простору в іншу неможливе. Зміни поля в деякій точці за законом у другій точці на віддалі 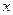від першої відбуваються за законом 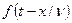, де - швидкість поширення взаємодії.

Якщо зміни електромагнітного поля за часом відбуваються за законом га­рмонічних коливань, наприклад , то зміни електромагнітної хвилі взагалі, при урахуванні зміни процесу не тільки за часом, але і в просторі зі швидкістю будуть проходити за законом 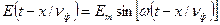. Відзначимо, що знак "мінус" при другій складовій аргументу вказує на відста­вання фази процесу в разі переміщення його із однієї точки в іншу. Величина 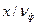має вимір часу, а тому складові та є рівноправними і визначають зміну процесу за часом і в просторі.

Розглянемо детальніше складову . Якщо до неї підставити значення дістанемо . Порівнюючи це співвідношення з , легко помітити, що величина виконує у виразі таку ж саму роль, як і величина у виразі . Оскільки , тобто є оберненою періоду, слід вважати, що - також обернена періоду зміни хвильового процесу, тільки в просторі. Тому називають довжиною хвилі, тобто відстанню, на якій фаза хвильового процесу змінюється в просторі на .

Величина , яка характеризує швидкість зміни процесу в просторі, називається хвильовим числом. Позначається для електромагнітних хвиль, які поширюються у вільному просторі, літерою латинської абетки . При розрахунках поширення електромагнітних хвиль напрямними системами (див. §8.4) хвильове число називають також коефіцієнтом фази і познача­ють . Вимірюється хвильове число в метрах у мінус першій степені (м^-1). З визначення хвильового числа випливає, що фазова швидкість

. (7.11)

Враховуючи введені позначення, хвильовий процес описується функцією

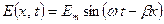. (7.12)

Відзначимо, що у формулі (7.12) записано вираз для модуля вектора електромагнітної хвилі. Якщо врахувати, що напруженість поля - величина векторна, формула (7.12) перепишеться у вигляді

. (7.13)

Як зазначено раніше, існування електромагнітного поля можливе лише тоді, коли та взаємно перпендикулярні. Тому

. (7.14)

Вектор Пойнтинга. Напрямок, в якому переміщується електромагнітна хвиля, залежить від взаємної орієнтації векторів та (див. міркування побудови рис. 7.4) і визначається правилом буравчика. Якщо буравчик розмістити в напрямку, перпендикулярному до векторів та , і крутити його від до найкоротшим шляхом, то напрямок переміщення буравчика покаже напрямок переміщення електромагнітної хвилі. Неважко впевнитись, що за зміни напрямку векторів та на зворотний, напрямок переміщення електромагнітної хвилі не зміниться.

Правило буравчика подає операцію з векторами, яку називають вектор­ним добутком двох векторів. Нагадаємо, що векторний добуток - це третій вектор , який перпендикулярний до векторів-співмножників і направлений у той бік, звідки повертання від першого вектора до другого найкоро­тшим шляхом відбувається за часовою стрілкою. Величина вектора дорів­нює добутку довжин векторів та на синус кута між ними. Таким чином, векторним добутком напруженостей та є третій вектор , який називає­ться вектором Пойнтинга.

. (7.15)

Напрямок , як це було зазначено раніше, показує напрямок поширення енергії, а величина його дорівнює густині потоку потужності. Вектор Пойн­тинга вимірюється у ватах на квадратний метр (Вт/м²).

Поляризація хвилі. Явища на межі розділу середовищ. Напрямки всіх трьох векторів, які характеризують електромагнітну хвилю, жорстко пов'язані між собою. Тому досить задати тільки напрямок двох із них, а для третього напрямок вже буде визначений. Наприклад, на рис. 7.5 вектор лежить у площині, яка проходить через вісь 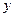, напрямок поширення - 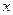. Цей факт прийнято пояснювати словами "хвиля поляризована в площині ". Отже, термін "поляризація хвилі" пов'язаний з орієнтацією вектора .

Особливо важливо визначати поляризацію у випадку падіння хвилі на межу розділу двох середовищ, де має місце відбиття та заломлення хвиль. Коефіцієнти відбиття та заломлення залежать як від кута падіння і парамет­рів середовищ, так і від орієнтації вектора відносно межі розділу середо­вищ (рис. 7.6). Будемо вважати площиною падіння площину, пер­пендикулярну до межі розділу, у цій площині лежить вектор Пойнтинга (напрямок поширення). У такому разі можливі дві принципово різні орієнтації вектора відносно пло­щини падіння; вектор перпендику­лярний до площини падіння та вектор лежить у цій площині. У першому випадку мова йде про поперечну , а в другому - про паралельну поляризації. У випадку довільної орієнтації відносно площини падіння можна розкласти вектор на два ортогональних (під кутом 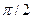) та . Явища на межі розділу середовищ визначаються законами Снелліуса і коефіцієнтами Френеля.

Закони Снелліуса пов'язують між собою кут падіння , кут заломлення та кут відбиття (рис. 7.6). Перший закон Снелліуса зазначає, що кут падіння дорівнює куту відбиття

.

Щоб сформулювати другий закон Снелліуса, нагадаємо, що показником заломлення середовища називають величину , де 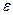, 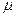- відносні електрична та магнітна проникності середовища. Для більшості середовищ , а тому вважають . Із урахуванням показника заломлення другий закон Снелліуса можна сформулювати так: відношен­ня синуса кута заломлення до синуса кута падіння дорівнює зворотному відношенню показників заломлення цих середовищ:

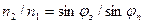, (7.16)

де - показники заломлення першого та другого середовищ.

Коефіцієнти Френеля, які надають співвідношення між амплітудами па­даючої, відбитої та заломленої хвиль, залежать від виду поляризації та хвильового опору середовища. Цей опір визначається для заданого середо­вища як відношення амплітуд напруженостей електричного та 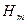магніт­ного 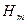полів хвилі.

Згідно з рівняннями Максвелла, хвильовий опір середовища поширення з діелектричною 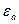та магнітною 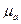проникностями

(7.17)

має активний характер. Наприклад, для вільного простору (вакууму, повітря)

Ом.

Як зазначено раніше, коефіцієнти Френеля залежать від поляризації:

для поперечної

; , (7.18)

для паралельної

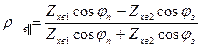; . (7.19)

Тут - коефіцієнт відбиття; 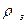- коефіцієнт заломлення; - хвильові опори середовищ; - кут падіння; - кут заломлення. За відо­мими коефіцієнтами Френеля з формул (7.18) та (7.19) амплітуди відбитої та заломленої хвиль обчислюються перемноженням амплітуди падаючої хвилі (електричної чи магнітної) на відповідний коефіцієнт.

Фронт хвилі. Поверхню однакових фаз називають фронтом хвилі. Якщо характер змін, що відбуваються в електромагнітному полі, описується функ­цією , то величина визначає фазу хвилі в просторі. Якщо її зафіксувати, то дістаємо рівняння . У прямокутній системі коорди­нат цьому рівнянню відповідає перпендикулярна до осі 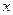площина, тому електромагнітні хвилі такого типу називають плоскими. Можливе існування циліндричних, сферичних та інших типів хвиль. Але, якщо розглядати неве­личку ділянку фронту електромагнітної хвилі будь-якого типу на великій віддалі від джерела, то його завжди можна вважати плоским (також як невелику ділянку Землі).

Date: 2016-02-19; view: 658; Нарушение авторских прав