Приклад 4.4. Знайти відгук НЕ з квадратичною ВАХ на дію

Для заданої дії відгук . Якщо використати тригонометричні формули 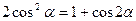та , дістанемо

.

Кількість комбінаційних частот у спектрі відгуку досить велика, у прин­ципі нескінченна. Але для їх простого обчислення використовується така закономірність: комбінаційні частоти можна подати у вигляді

, (4.11)

де - будь-які цілі додатні числа, а також і нуль. Для обчислень комбінаційні частоти зручно групувати, тобто об'єднувати ті частоти, для яких

, (4.12)

де - порядок комбінаційної частоти. Знак модуля у формулі (4.11) указує на той факт, що фізично існують тільки додатні частоти.

Розрахунки комбінаційних частот (їх частоти, амплітуди, фази) найпрос­тіше провадяться, якщо ВАХ нелінійного елемента описано поліномом. При цьому слід ураховувати важливу закономірність: складова полінома зі степе­нем дає змогу обчислити комбінаційні частоти з максимальним порядком . Якщо - парне число, то у відгуку обчислюються постійна складова та комбінаційні частоти парних порядків: . Якщо непарне число, то у спектрі відгуку обчислюються частоти дії та комбінаційні частоти непарних порядків .

Крім того, сума коефіцієнтів при частотах у формулі (4.11) повинна до­рівнювати порядку комбінаційної частоти .

Таким чином, комбінаційні частоти виникають під час одночасної дії на НЕ не менше двох гармонічних коливань із різними частотами.

Примітка При апроксимації ВАХ нелінійного елемента поліномом n-го степеня можна обчислити у відгуку НЕ, як це показано вище, комбінаційні частоти порядку. Але це не означає, що у відгуку НЕ нема комбінаційних частот більш високого порядку. Вони можуть бути, але для їх обчислення необхідно апроксимувати ВАХ нелінійного елемента поліномом більш високого степеня.

Приклад 4.5. ВАХ нелінійного елемента описана поліномом, який має квадратичний та кубічний члени. Вхідна дія складається з трьох гармонічних коливань з частотами. Обчислити частоти спектра відгуку НЕ.

Оскільки в опис ВАХ нелінійного елемента входять другий та третій степені полінома, то у спектрі відгуку будуть постійна складова, гармоніки і комбінаційні частоти як парного, так і непарного порядків з. Обчислення їх провадимо за співвідношенням (4.11). Частоти першого порядку:. Гармоніки та комбінаційні частоти другого порядку:. Гармоніки та комбінаційні частоти третього порядку:.

Якщо користуватись принципом комбінаційних частот, можна досить легко обчислити частоти спектра відгуку НЕ. Але амплітуди складових цього спектра обчислюються відносно просто тільки при невеликій кількості частот у вхідній дії (одна, дві).

Бігармонічна дія. Сигнал, що містить два гармонічних коливання з рі­зними частотами та амплітудами , в радіотехніці прийнято називати б/гармонічнім. Відгук НЕ на дію бігармонічого сигналу містить у собі різноманітні комбінаційні частоти, амплітуди яких можна знайти, якщо скористуватись тригонометричними формулами добутку косинусів. Результати обчислень у разі опису ВАХ нелінійного елемента поліномом до третього степеня включно зведені в табл. 4.2. Значення постійної скла­дової і амплітуд різних частот визначаються як сума елементів відповідних рядків табл. 4.2.

За формулами табл. 4.2 можна визначити і складові відгуку нелінійного кола на гармонічну дію. Для цього потрібно амплітуду коливання з частотою прийняти нульовою, тобто .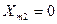

За допомогою аналогічних розрахунків можна знайти і спектральний склад відгуку безінерційного лінійно-параметричного елемента на полігармонічну дію. Слід відзначити, що при цьому спектральний склад відгуку значно простіший, оскільки в ньому відсутні гармоніки частот дії та комбі­наційні частоти біля них. Тому лінійно-параметричні елементи та кола широко використовуються для формування модульованих сигналів, для перетворення частоти тощо.

Date: 2016-02-19; view: 438; Нарушение авторских прав