Частотна залежність параметрів коаксіального кабелю КМ-4

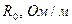
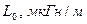
	0,0367 0,0687 0,0899 0,1070 0,1218 0,1349 0,1469 0,1579 0,1682 0,1741	0,257 0,257 0,257 0,257 0,257 0,257 0,257 0,257 0,257 0,257	47,5 47,5 47.5 47.5 47.5 47,5 47,5 47,5 47,5 47,5	0,143 0,0502 0,0860 0,1219 0,1577 0,1936 0,2295 0,2653 0,3012 0,3227

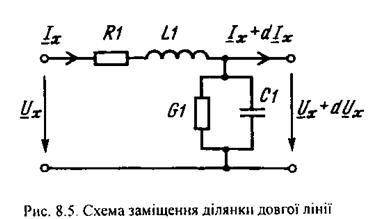
Переходимо тепер без­посередньо до побудови схеми заміщення лінії. Електричну схему лінії з генератором та навантажен­ням надано на рис. 8.4. Умовно поділимо лінію на каскадне сполучення елемен­тарних ділянок завдовжки . На рис. 8.4 виділена одна така ділянка на віддалі 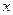від початку лінії. Якщо виходити з фізичних міркувань, малу ділянку лінії можна предста­вити у вигляді Г-подібної ланки, наведеної на рис.8.5. Елемент моделює опір провідників, — індуктив­ність провідників, ємність між провідниками,

- провідність ізоляції. Оскільки довжина ділянки лінії , то значення , , та просто знайти через первинні параметри: , , , .

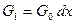Таким чином, схема заміщення лінії являє собою каскадне сполучення Г-подібних чотириполюсників, як це зображено на рис. 8.6.

7.3. ВТОРИННІ ПАРАМЕТРИ ЛІНІЇ

Хвильовий опір лінії. Розглянемо лінію (див. рис. 8.4) і знайдемо вхід­ний опір ділянки лінії завдовжки , якщо опір навантаження дорівнює деякому опору, позначеному як . Вхідний опір можна знайти як відно­шення напруги , до струму . Для цього поділимо почленно рівняння (8.17), тобто

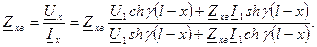(8.18)

Оскільки напруга та струм на навантаженні пов'язані законом Ома , то в рівнянні (8.18) другий співмножник буде дорівнювати одиниці, і тоді дістаємо цікавий результат: , тобто за умови вхідний опір не залежить від місця розміщення перерізу й дорівнює . Цей опір називається хвильовим. До речі, якщо лінію розглядати як чотириполюсник, то хвильовий опір є характеристичним.

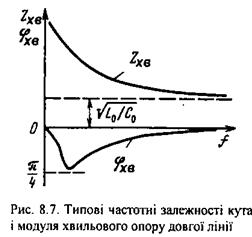Хвильовий опір визначається через первинні параметри за формулою (8.15). Для його розрахунків зручно виділити модуль та кут , типові залежності яких подано на рис. 8.7.

Існують наближені формули для роз­рахунків хвильового опору. Так, в області тональних частот справедливі нерівності та , і тоді

.

В області радіочастот, де 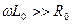та 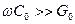, маємо

Коефіцієнт поширення. Для узго­дженого навантаження другі складові в рівняннях (8.14) будуть дорівнювати нулю, а перші набудуть вигляду:

. (8.19)

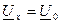Покладемо , тоді , та . В результаті дістаємо рівняння, які пов'язують напругу та струм на вході і виході лінії при узго­дженому навантаженні:

. (8.20)

Якщо формули (8.20) підставити в рівняння (8.19), то дістанемо співвідно­шення, які пов'язують напругу та струм на початку і в будь-якому перерізі лінії:

. (8.21)

Коефіцієнт називається коефіцієнтом поширення. Існують аналогічні рівняння для чотириполюсника:

, (8.22)

де 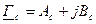- характеристична постійна передачі, - характеристич­не ослаблення (загасання); - характеристична фазова постійна; - напруга на вході та виході чотириполюсника відповідно.

Із порівняння виразів для лінії (8.20) та чотириполюсника (8.22) дістаємо ще один цікавий результат: є характеристичною постійною передачі лінії. Фізичний зміст коефіцієнта поширення є таким: - це характеристична постійна передачі лінії одиничної довжини. Характеристична постійна пере­дачі є комплексним числом і для даного випадку її можна представити як , де 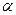- коефіцієнт ослаблення; - коефіцієнт фази, чи хвильове число.

У діапазоні тональних частот 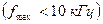, де та

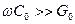
. (8.23)

У системах радіо- та багатоканального зв'язку лінії використовуються на частотах, де 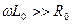та 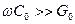. Наближені формули для цього випадку мають вигляд

(8.24)

(8.25)

Ці наближені формули застосовуються для розрахунків вторинних парамет­рів магістральних ліній зв'язку (коаксіальних та симетричних кабельних) і фіде­рів в їх робочій смузі частот. В області радіочастот, де 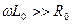та 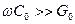, придатні для практики результати розрахунків дістаємо, якщо покласти та . Такі лінії називають лініями без втрат. У цьому випадку 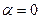, а обчис­люється за формулою (8.25). Якщо зробити числові розрахунки, одержуємо 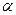в неперах на метр , а - у радіанах на метр . 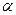Для того, щоб дістати в децибелах на метр , необхідно знайдені за формулами (8.23) чи (8.24) значення помножити на 8,69, оскільки .

Типові залежності коефіцієнта ослаб­лення 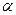та коефіцієнта фази подані на рис. 8.8. Частотна залежність вторин­них параметрів є істотною перешкодою для передачі сигналів, оскільки це призводить до лінійних спотворень - амплітудно-частотних та фазочастотних. Для зменшення лінійних спотворень застосовують спеціальні заходи.

Якщо відомі хвильовий опір та коефіцієнт поширення, за формулами (8.19) чи (8.21) можна знайти напругу та струм у будь-якому перерізі лінії, тобто ці величини повністю характеризують лінію і їх називають вторинни­ми параметрами лінії.

Date: 2016-02-19; view: 442; Нарушение авторских прав