
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

У нелінійних та параметричних колах
|
|
У системах зв'язку деякі корисні перетворення сигналів у процесі їх передавання каналами зв'язку пов'язані зі зміною спектрального складу. До таких перетворень належать випрямлення, модуляція та детектування, резонансне підсилення з великим ККД, множення, ділення та перетворення частоти тощо. Більшість із них здійснюються на передавальній стороні. Детектування, як правило, провадиться на приймальній стороні, де, крім корисного сигналу, завжди присутні завади.
У загальному випадку перетворення спектра сигналу можливе в колі, яке складено з джерела сигналу, нелінійного чи параметричного елемента і частотно-селективного навантаження у вигляді, наприклад, фільтра, який виділяє необхідну частоту чи смугу частот. Така схема перетворення сигналів та їх спектрів і розглядається далі.
5.1. МНОЖЕННЯ ЧАСТОТИ
Множення частоти - це процес підвищення частоти гармонічного коливання в ціле число разів. Необхідність у цьому виникає в тих випадках, коли формування коливань на потрібній частоті за якихось причин незручне. Наприклад, високостабільні кварцові генератори усталено працюють на частотах до ЗО МГц. При використанні множення частоти можна забезпечити кварцову стабілізацію частоти на більш високих частотах. У радіопередавачах каскади подвоєння та потроєння частоти є основними. Крім пониження частоти задавального генератора така побудова помітно зменшує зворотну дію більш потужних каскадів на попередні. Множення частоти з великою кратністю знаходить також широке застосування у фазометричних пристроях, еталонах частоти, генераторах сантиметрового діапазону та ін.
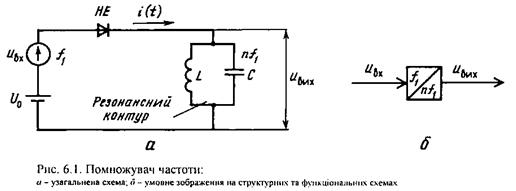 |
Принцип роботи помножувача частоти досить простий і його пояснює схема на рис. 6.1. У нелінійному колі діє гармонічне коливання
 . Форма струму
. Форма струму  через нелінійність діода значно відрізняється від гармонічного. А це означає, що спектр такого струму містить гармоніки з частотами, які кратні основній частоті
через нелінійність діода значно відрізняється від гармонічного. А це означає, що спектр такого струму містить гармоніки з частотами, які кратні основній частоті  . Корисною складовою струму при множенні є n-та гармоніка, на яку і настроюється вихідний LC-контур. Для цієї частоти контур має досить великий вхідний резонансний опір
. Корисною складовою струму при множенні є n-та гармоніка, на яку і настроюється вихідний LC-контур. Для цієї частоти контур має досить великий вхідний резонансний опір  вх0; для інших частот, у тому числі і основної
вх0; для інших частот, у тому числі і основної  , опір контура можна вважати рівним нулю, тому резонансний контур і виділяє необхідну гармоніку. Якщо змінювати частоту настройки контура, можна дістати різну кратність множення частоти. Крім резонансного контура, у помножувачах частоти застосовують інші селективні кола. Наприклад, у діапазоні сантиметрових хвиль застосовуються об'ємні резонатори з великою добротністю.
, опір контура можна вважати рівним нулю, тому резонансний контур і виділяє необхідну гармоніку. Якщо змінювати частоту настройки контура, можна дістати різну кратність множення частоти. Крім резонансного контура, у помножувачах частоти застосовують інші селективні кола. Наприклад, у діапазоні сантиметрових хвиль застосовуються об'ємні резонатори з великою добротністю.Амплітуда вихідної напруги помножувача частоти залежить від ВАХ нелінійного елемента та робочої точки на цій характеристиці
 (6.1)
(6.1)
де  - амплітуда струму n-ї гармоніки в колі.;
- амплітуда струму n-ї гармоніки в колі.;  вх0 - резонансний опір контура для n-ї гармоніки. Розрахункові формули для амплітуди струму гармонік залежать від способу апроксимації ВАХ. Наприклад, для кусково-лінійної апроксимації, згідно з виразами (4.6) та (6.1),
вх0 - резонансний опір контура для n-ї гармоніки. Розрахункові формули для амплітуди струму гармонік залежать від способу апроксимації ВАХ. Наприклад, для кусково-лінійної апроксимації, згідно з виразами (4.6) та (6.1),
 (6.2)
(6.2)
де  - коефіцієнти Берга;
- коефіцієнти Берга;  - кут відсічки;
- кут відсічки;  - крутість характеристики НЕ;
- крутість характеристики НЕ;  вхідний резонансний опір контура. Кут відсічки, для якого n-та гармоніка має максимальну амплітуду,
вхідний резонансний опір контура. Кут відсічки, для якого n-та гармоніка має максимальну амплітуду,  .
.
Але дістати великий коефіцієнт множення частоти одного каскаду з нелінійним елементом неможливо з двох причин: 1) величина струму гармонік різко зменшується з підвищенням їх кратності, крім того, деякі гармоніки взагалі можуть бути відсутні в залежності від виду ВАХ; 2) важко фільтрувати суміжні гармоніки (n - 1)-шу та (n + 1)-шу, які незначно відрізняються за частотою. Наявність цих гармонік призводить до появи паразитної амплітудної модуляції. Практично реалізуються в основному схеми подвоєння та потроєння частоти. Для одержання значного коефіцієнта множення (n = 103-105) застосовують багатокаскадні схеми, кожна з яких має невеликий коефіцієнт множення  . Загальний коефіцієнт множення всіх каскадів
. Загальний коефіцієнт множення всіх каскадів  .
.
Приклад 6.1. У потроювачі частоти (див. рис. 6.1,а) застосовано НЕ, ВАХ якого при  можна апроксимувати прямою з крутістю
можна апроксимувати прямою з крутістю  . Добротність контура
. Добротність контура  . Знайти амплітуду вихідної напруги, якщо до входу підведено напругу з амплітудою
. Знайти амплітуду вихідної напруги, якщо до входу підведено напругу з амплітудою  і частотою
і частотою  .
.
Вибираємо ємність контура за рекомендаціями, які наведено в прикладі 5.1 (2 пФ на метр довжини хвилі). Для частоти з  (довжина хвилі 5 м) С =10 пФ. Характеристичний опір контура
(довжина хвилі 5 м) С =10 пФ. Характеристичний опір контура 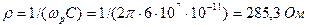 , звідки вхідний резонансний опір
, звідки вхідний резонансний опір  .
.
Для потроювача частоти оптимальний кут відсічки  . Із графіків рис. 4.8 знаходимо
. Із графіків рис. 4.8 знаходимо 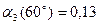 та, згідно з формулою (4.10),
та, згідно з формулою (4.10),  . За формулою (6.2) амплітуда напруги на виході потроювача частоти
. За формулою (6.2) амплітуда напруги на виході потроювача частоти 
5.2. ПЕРЕТВОРЕННЯ ЧАСТОТИ
Принцип перетворення частоти. Перетворенням частоти називають перенесення спектра модульованого сигналу з частоти переносника до деякої другої частоти, яка називається проміжною. При перетворенні частоти зберігаються амплітудні та фазові співвідношення між складовими спектра сигналу, змінюються тільки частоти складових, тобто перенесення спектра здійснюється без зміни закону модуляції.
Як відомо (див. §4.5), при підведенні до нелінійного елемента коливань із двома різними частотами  та
та  на його виході можна одержати комбінаційні складові з частотами суми
на його виході можна одержати комбінаційні складові з частотами суми  та різниці
та різниці  . Якщо селективним колом виділити тільки одну з них, наприклад різницеву, то це і буде коливання проміжної частоти
. Якщо селективним колом виділити тільки одну з них, наприклад різницеву, то це і буде коливання проміжної частоти  . Таким чином, якщо
. Таким чином, якщо  (
( - частота корисного сигналу), то для одержання проміжної частоти необхідне коливання від допоміжного генератора
- частота корисного сигналу), то для одержання проміжної частоти необхідне коливання від допоміжного генератора  . Цей генератор називається гетеродином. Як нелінійний елемент звичайно використовують безінерційний параметричний елемент, який називають змішувачем.
. Цей генератор називається гетеродином. Як нелінійний елемент звичайно використовують безінерційний параметричний елемент, який називають змішувачем.
Як змішувач використовуються різні електронні прилади, в яких напруги сигналу та гетеродина подають на той самий чи на різні електроди: біполярні транзистори, одно- чи багатосіткові лампи, польові транзистори з одним чи двома заслонами, диференціальні підсилювачі, кристалеві діоди (у НВЧ діапазоні) та ін.
Під впливом періодичної напруги гетеродина  значної величини диференціальна крутість ВАХ змішувача періодично змінюється. А періодичну функцію
значної величини диференціальна крутість ВАХ змішувача періодично змінюється. А періодичну функцію  можна розкласти в ряд Фур'є
можна розкласти в ряд Фур'є
 (6.3)
(6.3)
 |
де
 - коефіцієнти розкладання. Для практичних розрахунків у ряді (6.3) можна обмежитись двома складовими.
- коефіцієнти розкладання. Для практичних розрахунків у ряді (6.3) можна обмежитись двома складовими.
При подачі до входу перетворювача (рис. 6.2) модульованого сигналу, наприклад АМ, 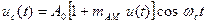 змінна складова вхідного струму згідно з рядом (6.3)
змінна складова вхідного струму згідно з рядом (6.3)

Цей вираз можна представити у вигляді
 (6.4)
(6.4)
Вихідна напруга перетворювача  пропорційна складовій різницевої частоти
пропорційна складовій різницевої частоти  у виразі (6.4), через те що на цю частоту настроєно коливальний контур у колекторному колі транзисторного перетворювача
у виразі (6.4), через те що на цю частоту настроєно коливальний контур у колекторному колі транзисторного перетворювача
 . (6.5)
. (6.5)
З виразу (6.5) випливає, що  є АМ сигналом за тим самим законом модуляції, що і вхідний АМ сигнал, маємо тільки зміщення частоти переносника. Це перетворення подане на рис. 6.3, де зображено спектри вхідного та вихідного сигналів перетворювача. Перенесення спектра вхідного сигналу на проміжну частоту означає, що коливальний контур перетворювача повинен мати смугу пропускання достатньою для неспотвореного передавання модульованого сигналу.
є АМ сигналом за тим самим законом модуляції, що і вхідний АМ сигнал, маємо тільки зміщення частоти переносника. Це перетворення подане на рис. 6.3, де зображено спектри вхідного та вихідного сигналів перетворювача. Перенесення спектра вхідного сигналу на проміжну частоту означає, що коливальний контур перетворювача повинен мати смугу пропускання достатньою для неспотвореного передавання модульованого сигналу.
Крутість перетворення. Ефективність роботи перетворювача прийнято характеризувати особливим параметром - крутістю перетворення  , яка дорівнює відношенню амплітуди струму проміжної частоти на виході перетворювача до амплітуди немодульованого сигналу на його вході
, яка дорівнює відношенню амплітуди струму проміжної частоти на виході перетворювача до амплітуди немодульованого сигналу на його вході


Для знаходження  треба знати залежність диференціальної крутості
треба знати залежність диференціальної крутості  від напруги гетеродина, знайти закон зміни за часом
від напруги гетеродина, знайти закон зміни за часом  під впливом напруги гетеродина, а потім розкласти
під впливом напруги гетеродина, а потім розкласти  у ряд Фур'є і обчислити амплітуду першої гармоніки. Це досить складна процедура. Але для практичних розрахунків можна вважати, що під впливом напруги гетеродина
у ряд Фур'є і обчислити амплітуду першої гармоніки. Це досить складна процедура. Але для практичних розрахунків можна вважати, що під впливом напруги гетеродина  змінюється від 0 до
змінюється від 0 до 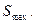 Тоді крутість перетворення
Тоді крутість перетворення  при гармонічній зміні
при гармонічній зміні  та
та  , при прямокутній зміні
, при прямокутній зміні  . Отже, у будь-якому режимі роботи перетворювача крутість перетворення має порядок
. Отже, у будь-якому режимі роботи перетворювача крутість перетворення має порядок
 (6.6)
(6.6)
яким і користуються для практичних розрахунків. При цьому слід враховувати, що максимальна крутість пропорційна амплітуді гетеродина.
Відношення амплітуди вихідної напруги сигналу на проміжній частоті до амплітуди сигналу на вході перетворювача є коефіцієнтом передачі (підсилення) перетворювача  пер. Як і для будь-якого резонансного підсилювача коефіцієнт підсилення перетворювача Кпер
пер. Як і для будь-якого резонансного підсилювача коефіцієнт підсилення перетворювача Кпер 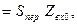 де
де  - вхідний резонансний опір контура. З формули (6.6) випливає, що коефіцієнт підсилення будь-якого каскаду в режимі перетворення частоти приблизно в 3-4 рази менший, ніж у режимі підсилення.
- вхідний резонансний опір контура. З формули (6.6) випливає, що коефіцієнт підсилення будь-якого каскаду в режимі перетворення частоти приблизно в 3-4 рази менший, ніж у режимі підсилення.
Розрахунки перетворювача частоти звичайно зводяться до знаходження частоти та амплітуди гетеродина, параметрів коливального контура, коефіцієнта передачі та вихідної напруги сигналу для заданого сигналу на вході та параметрів нелінійного елемента. Далі наведено приклад таких розрахунків.
Приклад 6.2. У перетворювачі частоти застосовано транзистор із максимальною диференціальною крутістю при. напруга запирання транзистора. До входу перетворювача подано АМ сигнал: частота переносника 1600 кГц, ширина спектра 6,8 кГц. Знайти частоту і амплітуду гетеродина, коефіцієнт передачі перетворювача на проміжній частоті.
За формулою (6.6) для гармонічного сигналу гетеродина знаходимо і. Таку крутість буде забезпечено, якщо напруга гетеродина займає всю робочу ділянку характеристики НЕ 0,3-0,9 В, звідси амплітуда напруги гетеродина.
Нехай частоту гетеродина розміщено вище за частоту сигналу, тобто, тоді. Для виділення спектра АМ сигналу зі смугою на проміжній частоті коливальний контур повинен мати добротність. Якщо прийняти і вибрати ємність контура (див. приклад 3.2), то вхідний резонансний опір коливального контура. Коефіцієнт передач, перетворювача.
Схемна побудова перетворювачів частоти. Розрізняють два варіанти схем перетворювачів частоти, в яких змішувач і гетеродин виконано у вигляді двох самостійних схем на різних активних елементах або об'єднано в одному активному елементі. Друга схема має гірші параметри в порівнянні зі схемою з окремим гетеродином, оскільки важко одночасно забезпечити оптимальні режими як для змішувача, так і для гетеродина. Тому на практиці частіше застосовуються схеми перетворювачів з окремим гетеродином.
Застосування перетворювачів частоти. У техніці електрозв'язку та радіоелектроніці перетворення частоти займає особливе місце. Це найбільш поширена операція при формуванні сигналів у радіопередавачах, апаратурі багатоканального зв'язку, радіоприймачах та ін. Застосування так званого супергетеродинного приймання дало можливість значно поліпшити якісні показники радіоприймачів. Використання в супергетеродинних приймачах принципу перенесення високої частоти до більш пониженої проміжної частоти дало можливість підсилювати та виділяти корисний сигнал простими вузькосмуговими підсилювачами проміжної частоти.
5.3. ДІЛЕННЯ ЧАСТОТИ
Ділення частоти - це процес зменшення частоти гармонічного коливання в ціле (чи дробне) число разів. Нині застосовуються два типи подільників частоти: двійкові та регенеративні.
Двійкові подільники будуються на двійкових дискретних елементах (тригерах). Кожний тригер у лічильному режимі зменшує частоту у два рази. Якщо побудувати ланцюжок із  тригерів та ввести в нього зворотні зв'язки, то можна дістати коефіцієнт ділення такої схеми
тригерів та ввести в нього зворотні зв'язки, то можна дістати коефіцієнт ділення такої схеми  . Подільники частоти на двійкових елементах вивчаються в курсі "Імпульсна техніка". Оскільки у двійкових подільниках частоти, як правило, застосовуються тригери на мікросхемах, то вони поширені в новітній апаратурі зв'язку.
. Подільники частоти на двійкових елементах вивчаються в курсі "Імпульсна техніка". Оскільки у двійкових подільниках частоти, як правило, застосовуються тригери на мікросхемах, то вони поширені в новітній апаратурі зв'язку.
Функціональну схему регенеративного подільника частоти подано на рис. 6.4. Ця схема аналогічна схемі автогенератора (див. рис. 5.1). Особливості: замість підсилювача застосовано змішувач, селектививне коло якого настроєне на частоту  , а у колі додатного зворотного зв'язку є помножувач частоти в т разів. У наведеній схемі напругу сигналу можна розглядати як напругу гетеродина для змішувача. Ділення частоти здійснюється в цій схемі через наявність змішувача та помножувача в замкнутому колі з додатним зворотним зв'язком.
, а у колі додатного зворотного зв'язку є помножувач частоти в т разів. У наведеній схемі напругу сигналу можна розглядати як напругу гетеродина для змішувача. Ділення частоти здійснюється в цій схемі через наявність змішувача та помножувача в замкнутому колі з додатним зворотним зв'язком.
 |
При відсутності сигналу на вході
 петльовий коефіцієнт передачі схеми можна вважати рівним нулю. Нагадаємо, що коефіцієнт передачі змішувача пропорційний амплітуді напруги гетеродина (у даному випадку - амплітуді напруги сигналу), тому на жодній частоті не виконується амплітудна умова самозбудження (5.4) і вихідна напруга у схемі
петльовий коефіцієнт передачі схеми можна вважати рівним нулю. Нагадаємо, що коефіцієнт передачі змішувача пропорційний амплітуді напруги гетеродина (у даному випадку - амплітуді напруги сигналу), тому на жодній частоті не виконується амплітудна умова самозбудження (5.4) і вихідна напруга у схемі  .
.
При подачі до входу змішувача гармонічного сигналу з амплітудою  та частотою
та частотою  петльовий коефіцієнт передачі схеми стає достатнім для виникнення автоколивань на частоті
петльовий коефіцієнт передачі схеми стає достатнім для виникнення автоколивань на частоті  настройки селективного кола 1. Для існування в розглянутій схемі з додатним зворотним зв'язком стаціонарного усталеного режиму ділення частоти, крім необхідних для будь-якого автогенератора балансу амплітуд та фаз, необхідно виконати ще й частотну умову: при діленні частоти в п разів коефіцієнт множення частоти повинен бути
настройки селективного кола 1. Для існування в розглянутій схемі з додатним зворотним зв'язком стаціонарного усталеного режиму ділення частоти, крім необхідних для будь-якого автогенератора балансу амплітуд та фаз, необхідно виконати ще й частотну умову: при діленні частоти в п разів коефіцієнт множення частоти повинен бути  .
.
Примітка. При діленні частоти на два (п = 2) помножувач у колі зворотного зв'язку не потрібен.
Регенеративні подільники частоти нині застосовуються в тих випадках, коли двійкові подільники працюють нестало, наприклад на НВЧ.
Принцип одержання дробового коефіцієнта ділення  досить простий: спочатку частота ділиться
досить простий: спочатку частота ділиться  разів, а далі множиться
разів, а далі множиться 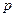 разів. Здійснювати ці операції у зворотному порядку - спочатку множення, а потім ділення небажано через складність схем помножувачів та подільників на більш високих частотах.
разів. Здійснювати ці операції у зворотному порядку - спочатку множення, а потім ділення небажано через складність схем помножувачів та подільників на більш високих частотах.
5.4 МОДУЛЯТОРИ ТАЇХ ХАРАКТЕРИСТИКИ
 |
Модуляція переносника здійснюється у спеціальних пристроях - модуляторах. За допомогою модуляторів фізично реалізуються операції, характерні для різних видів модуляції (див. розд. 3). Якісні показники модуляторів прийнято оцінювати за модуляційною характеристикою, під якою розуміють залежність відхилення інформаційного параметра переносника від дії постійної модулюючої напруги
 . При гармонічному переноснику в модуляційній характеристиці на осі ординат відкладається відхилення: амплітуди
. При гармонічному переноснику в модуляційній характеристиці на осі ординат відкладається відхилення: амплітуди  при АМ, частоти
при АМ, частоти  при ЧМ, фази
при ЧМ, фази  при ФМ (рис. 6.5). Звичайно ця характеристика визначається експериментальне для конкретної схеми модулятора (її також можна обчислити теоретично). Як для АМ, так і для ЧМ і ФМ модуляційна характеристика має бути лінійною (в ідеальному випадку). Відхилення від лінійної залежності свідчить про нелінійні спотворення. Саме за допустимою величиною нелінійних спотворень вибирають амплітуду модулюючого сигналу для кожної конкретної схеми модулятора.
при ФМ (рис. 6.5). Звичайно ця характеристика визначається експериментальне для конкретної схеми модулятора (її також можна обчислити теоретично). Як для АМ, так і для ЧМ і ФМ модуляційна характеристика має бути лінійною (в ідеальному випадку). Відхилення від лінійної залежності свідчить про нелінійні спотворення. Саме за допустимою величиною нелінійних спотворень вибирають амплітуду модулюючого сигналу для кожної конкретної схеми модулятора.
Частотні властивості модуляторів визначаються за частотною характеристикою, під якою розуміють залежність основного параметра модульованого сигналу від частоти модулюючого гармонічного сигналу (при постійній його амплітуді). Для гармонічного переносника такими основними параметрами є коефіцієнт модуляції 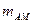 для АМ, девіація частоти
для АМ, девіація частоти  , для ЧМ та девіація фази
, для ЧМ та девіація фази  для ФМ. Частотна характеристика в ідеальному випадку має вигляд прямої, яка паралельна осі абсцис (частот) (рис. 6.6). Відхилення її від прямої дає можливість визначити як значення частотних спотворень модулятора, так і ефективну смугу частот модулюючого сигналу. Частотна характеристика модулятора також звичайно знаходиться експериментальне, і для її побудови на осі абсцис циклічна частота
для ФМ. Частотна характеристика в ідеальному випадку має вигляд прямої, яка паралельна осі абсцис (частот) (рис. 6.6). Відхилення її від прямої дає можливість визначити як значення частотних спотворень модулятора, так і ефективну смугу частот модулюючого сигналу. Частотна характеристика модулятора також звичайно знаходиться експериментальне, і для її побудови на осі абсцис циклічна частота  відкладається найчастіше в логарифмічному масштабі.
відкладається найчастіше в логарифмічному масштабі.
Практичні схеми модуляторів та їх характеристики навіть для того самого виду модуляції можуть бути різними в залежності від застосованих активних елементів, способу подання до них переносника та модулюючого сигналу. Так, для АМ розрізняють однотактні, двотактні, пасивні (на діодах), активні (на лампах, транзисторах) схеми модуляторів. У цьому розділі головну увагу зосереджено на принципах побудови модуляторів. Різні схемні рішення будуть вивчатись у спеціальних курсах.
5.5 АМПЛІТУДНІ, БАЛАНСНІ ТА ОДНОСМУГОВІ МОДУЛЯТОРИ
Амплітудні модулятори. З аналітичного виразу (математичної моделі) АМ сигналу (3.7), якщо його записати у вигляді
 , (6.7)
, (6.7)
випливає, що для формування АМ сигналу необхідно до переносника  додати добуток переносника і модулюючого сигналу з масштабним коефіцієнтом модуляції
додати добуток переносника і модулюючого сигналу з масштабним коефіцієнтом модуляції  . Структурну схему такого амплітудного модулятора зображено на рис 6.7.
. Структурну схему такого амплітудного модулятора зображено на рис 6.7.
 Із спектра АМ сигналу (3.9) випливає, що для його одержання необхідно сформувати три комбінаційні частоти (першого порядку
Із спектра АМ сигналу (3.9) випливає, що для його одержання необхідно сформувати три комбінаційні частоти (першого порядку  , другого порядку
, другого порядку  ). А оскільки комбінаційні частоти формуються НЕ, то якщо на НЕ з квадратичною ВАХ подати суму переносника
). А оскільки комбінаційні частоти формуються НЕ, то якщо на НЕ з квадратичною ВАХ подати суму переносника  і модулюючого сигналу
і модулюючого сигналу  , то можна дістати АМ сигнал. Схему такого найпростішого амплітудного модулятора з діодом як нелінійним елементом подано на рис. 6.8. Робоча точка вибирається на квадратичній ділянці ВАХ діода, тобто ВАХ діода можна описати як
, то можна дістати АМ сигнал. Схему такого найпростішого амплітудного модулятора з діодом як нелінійним елементом подано на рис. 6.8. Робоча точка вибирається на квадратичній ділянці ВАХ діода, тобто ВАХ діода можна описати як
 |
 , (6.8)
, (6.8)
де  - коефіцієнти апроксимації;
- коефіцієнти апроксимації;  - напруга, яку прикладено до діода. У схемі рис. 6.8
- напруга, яку прикладено до діода. У схемі рис. 6.8  і тоді
і тоді
 . (6.9)
. (6.9)
Для спрощення запису в формулі (6.9) аргумент 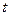 не записано. Виділені жирним шрифтом у формулі (6.9) складові утворюють АМ сигнал. Ці складові виділяються селективним колом (коливальним контуром, смуговим фільтром) із середньою частотою переносника
не записано. Виділені жирним шрифтом у формулі (6.9) складові утворюють АМ сигнал. Ці складові виділяються селективним колом (коливальним контуром, смуговим фільтром) із середньою частотою переносника  та смугою, яка дорівнює ширині спектра АМ сигналу. Напруга на виході коливального контура схеми на рис. 6.8 із вхідним резонансним опором
та смугою, яка дорівнює ширині спектра АМ сигналу. Напруга на виході коливального контура схеми на рис. 6.8 із вхідним резонансним опором  і буде АМ сигналом
і буде АМ сигналом
 .
.
 |
де
 - коефіцієнт зв'язку контура з колом діода через трансформатор
- коефіцієнт зв'язку контура з колом діода через трансформатор  . Хоч описаний модулятор і простий, але він не знайшов поширення в апаратурі зв'язку через малий рівень АМ сигналу на його виході, оскільки діоди мають незначну ділянку з квадратичною характеристикою.
. Хоч описаний модулятор і простий, але він не знайшов поширення в апаратурі зв'язку через малий рівень АМ сигналу на його виході, оскільки діоди мають незначну ділянку з квадратичною характеристикою.
Для підвищення рівня вихідного АМ сигналу діодний модулятор використовують часто в режимі великих значень  та
та  . Діод починає працювати з відсічкою струму. Принцип одержання амплітудної модуляції в цьому режимі пояснюється осцилограмами напруг та струмів, які подано на рис. 6.9. Для великого рівня сигналу ВАХ діода можна апроксимувати відрізками двох прямих. За рахунок того, що робоча точка переміщується модулюючим сигналом
. Діод починає працювати з відсічкою струму. Принцип одержання амплітудної модуляції в цьому режимі пояснюється осцилограмами напруг та струмів, які подано на рис. 6.9. Для великого рівня сигналу ВАХ діода можна апроксимувати відрізками двох прямих. За рахунок того, що робоча точка переміщується модулюючим сигналом  , здійснюється неперервна зміна амплітуди струму діода і, відповідно, кута відсічки. Тому амплітуда першої гармоніки послідовності імпульсів струму змінюється за часом. Напруга на коливальному контурі буде представляти собою АМ сигнал, тобто коливання з амплітудою, яка змінюється пропорційно модулюючому сигналу
, здійснюється неперервна зміна амплітуди струму діода і, відповідно, кута відсічки. Тому амплітуда першої гармоніки послідовності імпульсів струму змінюється за часом. Напруга на коливальному контурі буде представляти собою АМ сигнал, тобто коливання з амплітудою, яка змінюється пропорційно модулюючому сигналу  .
.
Детальний аналіз схеми показує, що при модуляції зміщенням робочої точки неможливо запобігти спотворенням АМ сигналу. Амплітудна модуляційна характеристика лінійна тільки для  .
.
З метою підвищення напруги вихідного АМ сигналу амплітудні модулятори виконують на активних елементах - транзисторах, лампах. Схемна побудова така сама, що і перетворювачів частоти. Напруги переносника і модулюючого сигналу подаються на базу (сітку). Амплітуда переносника має перевищувати амплітуду модулюючого сигналу. Контур схеми, який виконує роль фільтра, настроюється на частоту переносника і має смугу пропускання відповідно до ширини спектра АМ сигналу.
Балансний модулятор. Як випливає з аналітичного виразу БМ сигналу (3.10), для його формування необхідно виконати одну математичну операцію - перемноження переносника  і модулюючого сигналу
і модулюючого сигналу  . Структурну схему балансного модулятора зображено на рис. 6.10. Смуговий фільтр після перемножувача зі смугою пропускання, яка дорівнює ширині спектра БМ сигналу, включається для ослаблення зайвих складових на виході неідеального перемножувача.
. Структурну схему балансного модулятора зображено на рис. 6.10. Смуговий фільтр після перемножувача зі смугою пропускання, яка дорівнює ширині спектра БМ сигналу, включається для ослаблення зайвих складових на виході неідеального перемножувача.
 Модулятори ОМ сигналів. При всій різноманітності схем модуляторів ОМ сигналів у них реалізуються принципово два різні методи: фільтровий та фазовий.
Модулятори ОМ сигналів. При всій різноманітності схем модуляторів ОМ сигналів у них реалізуються принципово два різні методи: фільтровий та фазовий.
Фільтровий метод формування ОМ сигналу. Із визначення ОМ сигналу випливає, що для його формування необхідно із спектра амплітудне- чи балансно-модульованого сигналу виділити фільтром одну бокову смугу частот: верхню або нижню. Цей метод отримання ОМ сигналу називають фільтровим, і його структурну схему подано на рис. 6.11. Спочатку балансним модулятором формують двосмуговий БМ сигнал. Потім смуговими фільтрами СФ1 та СФ2 виділяють необхідну бокову смугу частот.
 |
Недолік цієї схеми в тому, що смугові фільтри мають досить малу смугу розфільтрації. Ця вимога випливає з того, що частотне рознесення між боковими смугами дорівнює
 при будь-якій частоті переносника
при будь-якій частоті переносника  . Як правило, при фільтровому методі формування ОМ сигналу застосовуються високодобротні п'єзокерамічні чи кварцові фільтри.
. Як правило, при фільтровому методі формування ОМ сигналу застосовуються високодобротні п'єзокерамічні чи кварцові фільтри.
Фазовий метод формування ОМ сигналу. Для отримання ОМ сигналу фазовим методом необхідно послідовно виконати всі операції, які подані в математичному описі ОМ сигналу (3.11)  : обчислити добуток переносника
: обчислити добуток переносника  і модулюючого сигналу
і модулюючого сигналу  ; перетворити сигнали
; перетворити сигнали  в
в 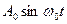 та
та  в
в  , для чого їх пропустити через фазообертачі з
, для чого їх пропустити через фазообертачі з
 |
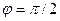 , обчислити добуток
, обчислити добуток 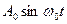 і
і  ; обчислити суму чи різницю отриманих добутків. У результаті дістаємо ОМ сигнал: на виході суматора - нижню бокову смугу частот, на виході віднімача - верхню бокову смугу частот. Схемну реалізацію такої послідовності операцій подано нарис. 6.12.
; обчислити суму чи різницю отриманих добутків. У результаті дістаємо ОМ сигнал: на виході суматора - нижню бокову смугу частот, на виході віднімача - верхню бокову смугу частот. Схемну реалізацію такої послідовності операцій подано нарис. 6.12.
5.6. ЧАСТОТНІ ТА ФАЗОВІ МОДУЛЯТОРИ
Частотна модуляція в автогенераторі. Для одержання лінійного відхилення частоти 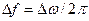 гармонічного коливання під дією модулюючого сигналу, що є характерним для ЧМ (див. §3.4), на частотах до 100 МГц широко застосовується безпосереднє керування частотою автогенератора. Оскільки частота коливань автогенератора (див. §5.3) визначається частотою настройки коливального контура, то для зміни генерованої частоти необхідно змінювати резонансну частоту контура.
гармонічного коливання під дією модулюючого сигналу, що є характерним для ЧМ (див. §3.4), на частотах до 100 МГц широко застосовується безпосереднє керування частотою автогенератора. Оскільки частота коливань автогенератора (див. §5.3) визначається частотою настройки коливального контура, то для зміни генерованої частоти необхідно змінювати резонансну частоту контура.
 Існує ряд методів перестроювання
Існує ряд методів перестроювання  чи
чи  контура: механічний, електромагнітний, електронний та ін. Для високої модулюючої частоти поширений безінерційний електронний метод керування ємністю контура. Для цього до контура підключають варикап - напівпровідниковий діод, ємність
контура: механічний, електромагнітний, електронний та ін. Для високої модулюючої частоти поширений безінерційний електронний метод керування ємністю контура. Для цього до контура підключають варикап - напівпровідниковий діод, ємність  переходу якого залежить від напруги, яку прикладено в напрямку запирання
переходу якого залежить від напруги, яку прикладено в напрямку запирання  переходу діода. Підключення варикапа VD до резонансного контура LС- автогенератора (індуктивна триточка) подано на рис. 6.13. Конденсатор Ср сполучає на високій частоті варикап VD з ємністю контура С, і його ємність вибирають такою, щоб опір конденсатора був малим на генерованій високій частоті та великим на частотах модулюючого сигналу
переходу діода. Підключення варикапа VD до резонансного контура LС- автогенератора (індуктивна триточка) подано на рис. 6.13. Конденсатор Ср сполучає на високій частоті варикап VD з ємністю контура С, і його ємність вибирають такою, щоб опір конденсатора був малим на генерованій високій частоті та великим на частотах модулюючого сигналу  . Початкова ємність варикапа
. Початкова ємність варикапа  (робоча точка на вольт-фарадній характеристиці) визначається напругою
(робоча точка на вольт-фарадній характеристиці) визначається напругою  , яка разом із модулюючою напругою
, яка разом із модулюючою напругою  підключається до варикапа через дросель Др. Дросель у схемі необхідний для розділення генерованої частоти від джерел зміщення та модулюючого сигналу. Модулююча напруга
підключається до варикапа через дросель Др. Дросель у схемі необхідний для розділення генерованої частоти від джерел зміщення та модулюючого сигналу. Модулююча напруга  змінює напругу на варикапі, тому змінюється ємність варикапа і, відповідно, генерована частота.
змінює напругу на варикапі, тому змінюється ємність варикапа і, відповідно, генерована частота.
Для заданих значень середньої частоти  та частотного відхилення
та частотного відхилення  необхідну зміну ємності
необхідну зміну ємності  можна дістати з формули резонансної частоти коливального контура:
можна дістати з формули резонансної частоти коливального контура:
 , (6.10)
, (6.10)
де  - середня ємність контура.
- середня ємність контура.
Якщо поділити вираз (6.10) на  , простими перетвореннями знаходимо
, простими перетвореннями знаходимо
 . (6.11)
. (6.11)
З виразу (6.11) випливає, що лінійній відносній зміні ємності  відповідає нелінійна зміна частоти
відповідає нелінійна зміна частоти  . Але, якщо відносна зміна частоти невелика
. Але, якщо відносна зміна частоти невелика  , то вираз можна спростити, знехтувавши величиною
, то вираз можна спростити, знехтувавши величиною 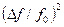 :
:
 . (6.12)
. (6.12)
Таким чином, при малих відносних змінах  та
та  пов'язані лінійною залежністю. Тому для одержання лінійної ЧМ ємність необхідно змінювати пропорційно миттєвим значенням модулюючого сигналу
пов'язані лінійною залежністю. Тому для одержання лінійної ЧМ ємність необхідно змінювати пропорційно миттєвим значенням модулюючого сигналу  . Знак "мінус" у формулі (6.12) означає, що при підвищенні ємності генерована частота зменшується.
. Знак "мінус" у формулі (6.12) означає, що при підвищенні ємності генерована частота зменшується.
Крім варикапів як керовані реактивні опори L чи С застосовують також спеціальні лампові чи транзисторні схеми, які називають відповідно реактивними лампами, або реактивними транзисторами. Але для них необхідно мати додаткові джерела живлення та фазозсуваючі кола. Нині реактивні лампи застосовуються рідко, реактивні транзистори отримали широке розповсюдження як складова частина мікросхем.
Фазова модуляція в резонансному підсилювачі. Для одержання ФМ необхідно мати пристрій, на виході якого фаза гармонічного коливання змінюється пропорційно модулюючому сигналу  . Одним з таких пристроїв може бути резонансний підсилювач з коливальним контуром як його навантаження, якщо змінювати частоту настройки контура. Для цього до контура підсилювача точнісінько так, як і до контура автогенератора (див. рис. 6.13), підключається варикап, який керується модулюючим сигналом. При зміні ємності варикапа відповідно змінюється резонансна частота контура, також і фаза вихідної напруги, тобто дістаємо фазову модуляцію. При цьому маємо паразитну амплітудну модуляцію, але її можна усунути амплітудним обмежувачем.
. Одним з таких пристроїв може бути резонансний підсилювач з коливальним контуром як його навантаження, якщо змінювати частоту настройки контура. Для цього до контура підсилювача точнісінько так, як і до контура автогенератора (див. рис. 6.13), підключається варикап, який керується модулюючим сигналом. При зміні ємності варикапа відповідно змінюється резонансна частота контура, також і фаза вихідної напруги, тобто дістаємо фазову модуляцію. При цьому маємо паразитну амплітудну модуляцію, але її можна усунути амплітудним обмежувачем.
Рівняння фазової характеристики контура з добротністю 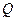 для невеликої розстройки
для невеликої розстройки  має вигляд
має вигляд  і з врахуванням виразу (6.12) дістаємо
і з врахуванням виразу (6.12) дістаємо
 . (6.13)
. (6.13)
Якщо  варикапа і відповідно
варикапа і відповідно  змінюється пропорційно модулюючому сигналу, то неспотворена ФМ має місце тоді, коли зміна
змінюється пропорційно модулюючому сигналу, то неспотворена ФМ має місце тоді, коли зміна  пропорційна
пропорційна  , тобто на лінійній ділянці фазової характеристики (6.13), де
, тобто на лінійній ділянці фазової характеристики (6.13), де  . Це справедливо тільки для індексу модуляції, який не перевищує 0,3-0,4 рад. Збільшення індексу модуляції можна одержати помноженням частоти.
. Це справедливо тільки для індексу модуляції, який не перевищує 0,3-0,4 рад. Збільшення індексу модуляції можна одержати помноженням частоти.
5.6. ФОРМУВАННЯ СИГНАЛІВ З ІМПУЛЬСНИМИ МОДУЛЯЦІЯМИ
Методи формування. Імпульсні види модуляції, часові діаграми яких зображено на рис. 3.13, можна дістати прямими та непрямими методами. Прямі методи здійснюються тими самими схемами, що й аналогові модуляції з невеликими змінами: як переносник  використовується послідовність імпульсів необхідної форми,
використовується послідовність імпульсів необхідної форми,
 |
тривалості, частоти, а замість селективного кола на виході модулятора включається резистивне навантаження. Це пов'язано з досить широким спектром імпульсних модуляцій (див. § 3.6). Непрямі методи засновано на перетворенні одного виду модуляції в інший, у тому числі аналогової в імпульсну.
 Амплітудно-імпульсна модуляція. Найчастіше застосовується прямий метод формування АІМ. Для цього використовується будь-яка схема амплітудного модулятора, наприклад діодного (див. рис. 6.8), який працює в режимі з
Амплітудно-імпульсна модуляція. Найчастіше застосовується прямий метод формування АІМ. Для цього використовується будь-яка схема амплітудного модулятора, наприклад діодного (див. рис. 6.8), який працює в режимі з
відсічкою. Замість діодів в амплітудноімпульсних модуляторах застосовують також транзистори, мікросхеми.
Частотіно-імпульсна модуляція. Якщо керувати частотою будь-якого релаксаційного автогенератора, наприклад мультивібратора чи блокінг-генератора, дістаємо ЧІМ. Для зміни частоти імпульсів, як і в генераторі гармонічних коливань, необхідно змінювати параметри коливального кола. Крім зміни ємності варикапами, у релаксаційних автогенераторах також застосовуються керовані резистори, оскільки вони забезпечують більші лінійність та межі зміни частоти.
Непрямий метод отримання ЧІМ заснований на перетворенні ЧМ у ЧІМ (рис. 6.16). Для цього ЧМ сигнал  пропускають через обмежувач за максимумом та мінімумом із досить малими порогами обмеження. З вихідних трапецієвих імпульсів ШІМ
пропускають через обмежувач за максимумом та мінімумом із досить малими порогами обмеження. З вихідних трапецієвих імпульсів ШІМ  диференціюванням та обмеженням одержуємо передні фронти. Це і є ЧІМ сигнал, частота імпульсів якого змінюється пропорційно модулюючому сигналу.
диференціюванням та обмеженням одержуємо передні фронти. Це і є ЧІМ сигнал, частота імпульсів якого змінюється пропорційно модулюючому сигналу.
Широтно-імпульсна та фазо-імпульсна модуляції. Одним із простих, але широко розповсюджених методів формування ШІМ та ФІМ є одержання їх з АІМ. Цей процес пояснюється часовими діаграмами на рис. 6.17. Як переносник для АІМ використовується періодична послідовність трикутних імпульсів (6.17, б). Якщо вихідний АІМ сигнал (6.17, в) пропустити через обмежувач за максимумом із низьким порогом обмеження, то на виході обмежувача дістаємо трапецієві імпульси ШІМ (6.17, г). Крутість фронтів імпульсів залежить від порога обмежувача. Якщо потім з одержаного ШІМ сигналу, як і в прикладі непрямого одержання ЧІМ, диференціюванням і обмеженням виділити передні фронти, то дістанемо сигнал із ФІМ (6.17, д), зсув імпульсів якого відносно центра трикутних імпульсів (6.17, 6) пропорційний модулюючому сигналу.
5.8. МАНІПУЛЯЦІЯ ПЕРЕНОСНИКА
 Будь-яка маніпуляція (дискретна модуляція) переносника є окремим випадком аналогової модуляції (див. розд. 3.5), тому всі методи та схеми формування аналогових видів модуляції повністю придатні і для формування маніпульованих сигналів, якщо послідовність стандартних елементів дискретного первинного сигналу
Будь-яка маніпуляція (дискретна модуляція) переносника є окремим випадком аналогової модуляції (див. розд. 3.5), тому всі методи та схеми формування аналогових видів модуляції повністю придатні і для формування маніпульованих сигналів, якщо послідовність стандартних елементів дискретного первинного сигналу  застосовувати як модулюючий сигнал. Якщо
застосовувати як модулюючий сигнал. Якщо  - двійковий сигнал, то він може приймати два значення:
- двійковий сигнал, то він може приймати два значення:  - двополярний сигнал чи
- двополярний сигнал чи  - однополярний сигнал (див. рис. 1.2). В аналогових модуляторах слід застосовувати двополярний модулюючий сигнал.
- однополярний сигнал (див. рис. 1.2). В аналогових модуляторах слід застосовувати двополярний модулюючий сигнал.
Якщо врахувати дискретний характер модулюючого та модульованого сигналів, то можна здійснити дискретні види модуляції з кращою якістю принципово іншим методом: сформувати спеціальними пристроями (наприклад, автогенераторами  ) дискретні сигнали
) дискретні сигнали  і далі комутувати їх керованими ключами відповідно до послідовності дискретних первинних сигналів
і далі комутувати їх керованими ключами відповідно до послідовності дискретних первинних сигналів  (рис. 6.18).
(рис. 6.18).
Ключові схеми формування маніпульованих сигналів нині є основними, оскільки вони дають змогу одержати з високою точністю дискретні сигнали 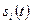 з раніше встановленими параметрами та властивостями. Як ключі застосовують діоди, транзистори, спеціальні мікросхеми. Головні вимоги до ключів - неспотворене передавання сигналів
з раніше встановленими параметрами та властивостями. Як ключі застосовують діоди, транзистори, спеціальні мікросхеми. Головні вимоги до ключів - неспотворене передавання сигналів  зі входу на вихід та відсутність проходження керуючого сигналу
зі входу на вихід та відсутність проходження керуючого сигналу  на вихід, тобто схема ключа має бути балансною для
на вихід, тобто схема ключа має бути балансною для  . Тому як ключі нині широко застосовуються аналогові перемножувачі сигналів. Зокрема, для формування ФМ-2 майже завжди застосовуються балансні модулятори.
. Тому як ключі нині широко застосовуються аналогові перемножувачі сигналів. Зокрема, для формування ФМ-2 майже завжди застосовуються балансні модулятори.
Формування ВФМ-2. Для одержання ВФМ-2 можна використати будь-яку схему формування ФМ-2, тільки перед фазовим маніпулятором у коло модулюючого дискретного сигналу включається спеціальний кодуючий пристрій, який забезпечує необхідне правило формування ВФМ-2 (див. §3.5): зміна фази переносника має місце тільки під час передавання одиниць дискретної послідовності  . Цей кодуючий пристрій називається відносним кодером.
. Цей кодуючий пристрій називається відносним кодером.
Структурну схему відносного кодера для однополярної дискретної послідовності первинного сигналу подано на рис. 6.19, а. Кодер має два блоки: суматор за модулем два А/2 та лінію затримки на тривалість елемента сигналу  . Роботу схемі можна простежити за часовими діаграмами на рис. 6.19, б, де цифрами показано форму сигналів у різних точках схеми. До входу 1 надходить послідовність дискретних однополярних елементів сигналу
. Роботу схемі можна простежити за часовими діаграмами на рис. 6.19, б, де цифрами показано форму сигналів у різних точках схеми. До входу 1 надходить послідовність дискретних однополярних елементів сигналу  , які позначено як 1 та 0. Нагадаємо правило додавання за модулем два:
, які позначено як 1 та 0. Нагадаємо правило додавання за модулем два: 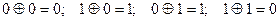 . Відповідно до цього правила суматор М2 додає дискретні сигнали зі входу 1 та з лінії затримки 2. Нахиленими стрілками на графіках показано затримку сигналу 3 на час
. Відповідно до цього правила суматор М2 додає дискретні сигнали зі входу 1 та з лінії затримки 2. Нахиленими стрілками на графіках показано затримку сигналу 3 на час  для одержання сигналу 2.
для одержання сигналу 2.
 |
Легко простежити, що якщо вихідний сигнал відносного кодера подати на фазовий модулятор, то фаза переносника на його виході буде змінюватись згідно з правилом ВФМ-2. Зазначимо, що для ФМ-2 фаза переносника змінюється при переході модулюючого сигналу від 0 до 1 та при зворотному переході. На часовій діаграмі зірочками позначено моменти часу, де має змінюватись фаза при ВФМ-2 (графік /) та де вона змінюється, якщо на фазовий маніпулятор подати керуючий сигнал із виходу відносного кодера (графік 3). Вони збігаються.
Date: 2016-02-19; view: 960; Нарушение авторских прав