
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розділ 6. Електромагнітні хвилі
|
|
6.1. ПОНЯТТЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ
Електричне та магнітне поля. Людство познайомилось з електричними та магнітними явищами досить давно. У Китаї магніт, як "камінь, що вказує напрямок", відомий був за тисячу років до н. е. Електричні властивості натертого янтарю були відомі стародавньому грецькому філософу Фалету Мілетському, який жив у V ст. до н.е. Але всі відомості про електричні та магнітні явища до XVI ст. мали дослідний характер зовнішніх проявлень, з якими людина зустрічалась у своєму повсякденному житті. З кінця XVI ст. вивчення електрики та магнетизму ставиться вже на наукову базу. Відтоді був накопичений величезний експериментальний матеріал, який дав можливість сформулювати ряд законів, що описують електричні та магнітні явища.
У 1873 р. англійський математик і фізик Джеймс Кларк Максвелл у своїй класичній праці "Трактат з електрики та магнетизму" виклав основи сучасної теорії електромагнітного поля, яке описується системою рівнянь, що надалі названі його іменем – рівняннями Максвелла.
У фізиці вважається, що можливі дві форми існування матерії: речовина і поле. Речовину ми уявляємо собі як сукупність різних часток – молекул, атомів та інших елементарних часток. Поле – особлива форма матерії, яка характеризується тільки їй притаманними рисами. Але незважаючи на те, що речовина та поле є різними формами існування матерії, вони мають ряд однакових властивостей. Так, електромагнітне поле, яке поширюється у просторі, може бути подане як потік дискретних часток – фотонів. І речовина, і поле характеризуються енергією, масою тощо.
Типи електромагнітних полів. Всю сукупність електромагнітних явищ можна поділити на кілька окремих випадків. Найпростішим є такий, для якого електромагнітне поле не залежить від часу, а джерела поля не переміщуються в просторі. Такі поля називаються статичними. Як відомо, джерелами електростатичного поля є електричні заряди, які не змінюють своєї величини та місця розташування. Джерела магнітостатичного поля – постійні нерухомі магніти. У зв'язку з тим, що статичні поля породжуються різними джерелами, вони можуть існувати незалежно одне від одного.
Постійний електричний струм створює електромагнітне поле, яке називають стаціонарним. У ньому електричне та магнітне поля вже не можна вважати незалежними, оскільки вони породжуються спільним джерелом – упорядкованим рухом вільних зарядів. Слід відзначити, що структура стаціонарного електромагнітного поля не залежить від часу, хоч воно й створене рухомими зарядами.
Найбільш загальним є змінне електромагнітне поле, яке створюється змінним струмом. Це поле змінюється за часом і переміщується у просторі, при цьому воно переносить частину енергії джерела. Саме цю властивість змінного електромагнітного поля й використовують для передавання сигналів в електрозв'язку.
Основні характеристики електромагнітного поля. Як зазначено раніше, джерелами поля є струми та заряди. Електричні заряди діють один на інший з силою  , що визначається законом Кулона:
, що визначається законом Кулона:
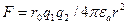 , (7.1)
, (7.1)
де  - величини зарядів;
- величини зарядів; 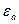 - абсолютна електрична проникність середовища, в якому розміщено заряди;
- абсолютна електрична проникність середовища, в якому розміщено заряди;  - відстань між зарядами.
- відстань між зарядами.
У формулі (7.1) силу взаємодії позначено літерою  і набрано напівжирним шрифтом. Так прийнято позначати векторні величини. Для повної характеристики вектора недосить знати його величину, необхідно також визначити його напрямок. Вказівка напрямку подається за допомогою спеціального вектора, який називають ортом, і він має одиничну довжину. Орт
і набрано напівжирним шрифтом. Так прийнято позначати векторні величини. Для повної характеристики вектора недосить знати його величину, необхідно також визначити його напрямок. Вказівка напрямку подається за допомогою спеціального вектора, який називають ортом, і він має одиничну довжину. Орт 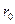 у формулі (7.1) показує, що сила спрямована вздовж прямої, яка з'єднує заряди. Якщо величину одного із зарядів, наприклад другого, прийняти за одиницю (
у формулі (7.1) показує, що сила спрямована вздовж прямої, яка з'єднує заряди. Якщо величину одного із зарядів, наприклад другого, прийняти за одиницю ( ), то ми зможемо визначити, з якою силою заряд діє на одиничний заряд, що розміщений у даній точці. Цю силу прийнято називати напруженістю електричного поля і її позначають
), то ми зможемо визначити, з якою силою заряд діє на одиничний заряд, що розміщений у даній точці. Цю силу прийнято називати напруженістю електричного поля і її позначають  . Із формули (7.1) видно, що вона, як і сила
. Із формули (7.1) видно, що вона, як і сила  , величина векторна. Напруженість у різних точках поля можна охарактеризувати за допомогою силових ліній, у кожній точці яких
, величина векторна. Напруженість у різних точках поля можна охарактеризувати за допомогою силових ліній, у кожній точці яких  дотична до силової лінії. Зазначимо, що густина силових ліній пропорційна величині
дотична до силової лінії. Зазначимо, що густина силових ліній пропорційна величині  .
.
З формули (7.1) випливає, що  , а також і
, а також і  , залежать від параметрів середовища, в якому розміщено джерела поля. Для того, щоб виключити вплив параметрів середовища на характеристики електромагнітного поля, вводиться вектор електромагнітної індукції
, залежать від параметрів середовища, в якому розміщено джерела поля. Для того, щоб виключити вплив параметрів середовища на характеристики електромагнітного поля, вводиться вектор електромагнітної індукції 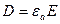 .
.
Отже, електричне поле є векторним і для його опису застосовуються два вектори  та
та 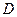 , які визначаються за силовою дією поля на одиничний нерухомий точковий заряд. Зазначимо, що
, які визначаються за силовою дією поля на одиничний нерухомий точковий заряд. Зазначимо, що  вимірюється у вольтах на метр (В/м), а
вимірюється у вольтах на метр (В/м), а 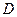 - у кулонах на квадратний метр (Кл/м2).
- у кулонах на квадратний метр (Кл/м2).
Аналогічно вводяться вектори Н та В за силовою дією магнітного поля на рухомий електричний заряд. Напруженість магнітного поля  вимірюється в амперах на метр (А/м), а магнітна індукція
вимірюється в амперах на метр (А/м), а магнітна індукція 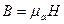 у теслах, або веберах на квадратний метр (Тл, або Вб/м2).
у теслах, або веберах на квадратний метр (Тл, або Вб/м2).
У загальному випадку, коли джерелом поля є змінний за часом струм, напруженості (індукції) поля є векторними функціями чотирьох змінних:
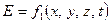 ;
; 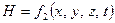 (7.2)
(7.2)
де 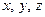 - координати точки, в якій визначаються
- координати точки, в якій визначаються  та
та  ;
; 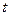 - час. Векторні поля, що описуються функціями (7.2), можуть бути двох основних типів – потенціальними (або безвихровими) та вихровими (або соленоїдними). Силові лінії потенціального поля завжди починаються її закінчуються на джерелах, силові лінії вихрового поля – це замкнуті лінії. Електростатичне поле завжди є потенціальним, а змінне електромагнітне поле в загальному випадку - сукупність потенціального поля електричних зарядів та вихрового поля індукції. Магнітне поле завжди вихрове, оскільки в природі відсутні магнітні заряди.
- час. Векторні поля, що описуються функціями (7.2), можуть бути двох основних типів – потенціальними (або безвихровими) та вихровими (або соленоїдними). Силові лінії потенціального поля завжди починаються її закінчуються на джерелах, силові лінії вихрового поля – це замкнуті лінії. Електростатичне поле завжди є потенціальним, а змінне електромагнітне поле в загальному випадку - сукупність потенціального поля електричних зарядів та вихрового поля індукції. Магнітне поле завжди вихрове, оскільки в природі відсутні магнітні заряди.
Електромагнітна індукція. Друге рівняння Максвелла. Візьмемо замкнутий провідник (його називають виток) (рис. 7.1) і ввімкнемо до нього мікроамперметр. Він буде показувати електричний струм кожного разу, коли змінюється магнітний потік  , що пронизує виток. Якщо поле в межах витка рівномірне, то
, що пронизує виток. Якщо поле в межах витка рівномірне, то
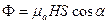 ,
,
де 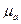 - абсолютна магнітна проникність середовища;
- абсолютна магнітна проникність середовища;  - напруженість поля;
- напруженість поля;  - площа витка;
- площа витка; 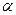 - кут між
- кут між  і нормаллю
і нормаллю 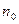 до площини витка. Якщо
до площини витка. Якщо  розподілена на площині витка нерівномірно, то
розподілена на площині витка нерівномірно, то
 , (7.3)
, (7.3)
де вектор 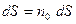 . Крапкою між векторами
. Крапкою між векторами  та
та  позначено скалярний добуток векторів.
позначено скалярний добуток векторів.
 Для виникнення струму причина зміни
Для виникнення струму причина зміни  неістотна: буде це пов'язано чи зі зміною напруженості магнітного поля
неістотна: буде це пов'язано чи зі зміною напруженості магнітного поля  , чи з переміщенням витка в магнітному полі. Напрямок струму у витку буде різним залежно від того, збільшується чи зменшується число силових ліній, що пронизують виток. Наявність струму у витку можна пояснити діючою там ЕРС, причому напрямок її дії визначається підвищенням чи зменшенням магнітного потоку. Якщо вважати, що виток плоский і
, чи з переміщенням витка в магнітному полі. Напрямок струму у витку буде різним залежно від того, збільшується чи зменшується число силових ліній, що пронизують виток. Наявність струму у витку можна пояснити діючою там ЕРС, причому напрямок її дії визначається підвищенням чи зменшенням магнітного потоку. Якщо вважати, що виток плоский і 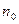 направлене так само, як і
направлене так само, як і  , то всі ділянки витка будуть знаходитись в однакових умовах. Тому розглянута ЕРС не є зосередженою, вона діє на всіх ділянках витка, тобто є розподіленою.
, то всі ділянки витка будуть знаходитись в однакових умовах. Тому розглянута ЕРС не є зосередженою, вона діє на всіх ділянках витка, тобто є розподіленою.
З електротехніки відомо, що існування струму в провіднику неможливе без електричного поля. А в розглянутому прикладі єдиною причиною виникнення струму була зміна магнітного поля. Отже, зміна магнітного поля, що пронизує виток, викликає у ньому електричне, попе, яке і є першопричиною виникнення струму. Діюче на всьому витку електричне поле виконує роль ЕРС, і її називають ЕРС індукції. Силові лінії цього поля являють собою замкнуті лінії (штрихова лінія на рис. 7.1).
Якщо виходити з того, що за фізичною суттю ЕРС - робота, то можна записати
 , (7.4)
, (7.4)
де 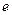 - ЕРС, що наводиться у витку;
- ЕРС, що наводиться у витку;  - вектор напруженості електричного поля у витку;
- вектор напруженості електричного поля у витку;  ;
; 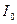 - орт, дотичний до витка у будь-якій його точці;
- орт, дотичний до витка у будь-якій його точці; 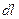 - елемент контура Г. Крім того, згідно із законом електромагнітної індукції Фарадея, ЕРС індукції
- елемент контура Г. Крім того, згідно із законом електромагнітної індукції Фарадея, ЕРС індукції
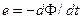 . (7.5)
. (7.5)
Якщо об'єднати вирази (7.4) і (7.5) та врахувати формулу (7.3), дістанемо
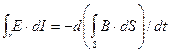 . (7.6)
. (7.6)
Вираз (7.6) узагальнює закон електромагнітної індукції Фарадея і є другім рівнянням Максвелла. З розглянутого прикладу, що вивів нас до другого рівняння Максвелла, випливає, що провідник витка у виникненні струму не має принципового значення. Він тільки допомагає виявити електричне поле, яке при цьому виникає. Отже, електричне поле буде індукуватись не тільки в контурі з провідником, а також у будь-якому умовному контурі, що не містить у собі провідників й знаходиться у будь-якому середовищі, у тому числі й у вакуумі. З виразу (7.6) можна зробити висновок, що змінне в деякій області простору магнітне поле породжує в тій самій області електричне поле, напруженість якого пропорційна швидкості зміни напруженості магнітного поля.
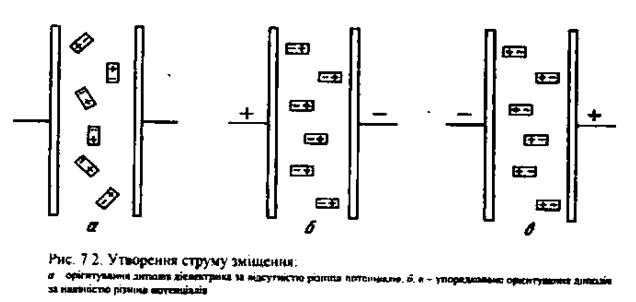
Струм зміщення. Перше рівняння Максвелла. Розглянемо плоский конденсатор (рис. 7.2). Нехай проміжок між пластинами буде заповнений поляризованим діелектриком. Це обмеження не знижує загальності міркувань, а тільки дещо спрощує картину процесу. Нагадаємо, що в першому наближенні поляризований діелектрик - це сукупність атомів та молекул, в яких орбіти руху електронів сильно витягнуті. Отже, речовину діелектрика можна представити у вигляді набору диполів (рис. 7.2, а). Оскільки до пластин конденсатора не прикладено різницю потенціалів, орієнтація диполів довільна.
Якщо до пластин конденсатора прикласти різницю потенціалів, то в діелектрику утвориться зовнішнє електричне поле 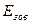 , під дією якого всі диполі повернуться навколо своєї осі і займуть положення, яке показано на рис. 7.2, б. Якщо на пластинах конденсатора змінити полярність зарядів (рис. 7.2, в), то диполі обернуться на 180°.
, під дією якого всі диполі повернуться навколо своєї осі і займуть положення, яке показано на рис. 7.2, б. Якщо на пластинах конденсатора змінити полярність зарядів (рис. 7.2, в), то диполі обернуться на 180°.
Розмістимо уявно в діелектрику площину, паралельну пластинам. Можна стверджувати, що при зміні полярності на пластинах конденсатора цю площину будуть перетинати пов'язані з атомами (молекулами) заряди. Але ж упорядкований рух зарядів називають струмом. Отже, через проведену в діелектрику площину буде проходити струм, який відрізняється від струму провідності тим, що являє собою упорядкований рух зв'язаних електричних зарядів. Його називають струмом зміщення. Наявність цього струму викликає появу магнітного поля.
Розглянута картина утворення струму зміщення відображає процес, який має місце в будь-якому діелектрику, крім вакууму (там відсутні поляризовані атоми і молекули). Але можна стверджувати, що як і при розгляданні електромагнітної індукції виток провідника не був принципово необхідним, так само діелектрик між пластинами конденсатора виконує допоміжну роль: він допомагає виявити магнітне поле. Таким чином, змінне за часом електричне поле еквівалентне дії електричного струму. Отже, можна стверджувати, що магнітне поле може виникати при дії як струму провідності, так і струму зміщення. Математичний запис цього ствердження називається першим рівнянням Максвелла:
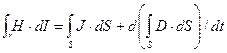 , (7.7)
, (7.7)
де 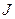 - вектор об'ємної густини струму провідності, він направлений перпендикулярно площині поперечного перерізу провідника;
- вектор об'ємної густини струму провідності, він направлений перпендикулярно площині поперечного перерізу провідника; 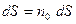 - вектор елемента площадки
- вектор елемента площадки  ;
; 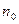 - нормаль до площадки
- нормаль до площадки  . Перша складова правої частини рівняння (7.7) - струм провідності, а друга - струм зміщення.
. Перша складова правої частини рівняння (7.7) - струм провідності, а друга - струм зміщення.
Зазначимо аналогію між явищем електромагнітної індукції та виникненням магнітного поля під дією струму зміщення. Слід звернути увагу на те, що збуджуюче поле і породжуване ним поле завжди взаємно перпендикулярні. Єдиною різницею у двох розглянутих випадках є протилежний напрямок виникаючих полів (різні знаки похідних).
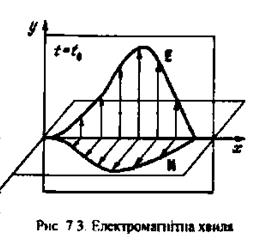 Виникнення електромагнітної хвилі. Нехай в деякій частині простору існує змінне за часом електромагнітне поле (рис. 7.3). Напруженість електричного поля орієнтована вздовж осі
Виникнення електромагнітної хвилі. Нехай в деякій частині простору існує змінне за часом електромагнітне поле (рис. 7.3). Напруженість електричного поля орієнтована вздовж осі 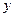 , а її величина залежить тільки від однієї координати в просторі -
, а її величина залежить тільки від однієї координати в просторі - 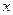 . Напруженість магнітного поля орієнтована вздовж осі
. Напруженість магнітного поля орієнтована вздовж осі  , а її величина залежить також тільки від
, а її величина залежить також тільки від 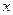 . Якщо вектори
. Якщо вектори  та
та  мають іншу орієнтацію, то через їх перпендикулярність до розглянутої орієнтації можна прийти поворотом осей декартової системи координат. Для простоти міркувань будемо вважати, що
мають іншу орієнтацію, то через їх перпендикулярність до розглянутої орієнтації можна прийти поворотом осей декартової системи координат. Для простоти міркувань будемо вважати, що  та
та  не змінюють своєї орієнтації. Жирні криві на рис. 7.3 є обвідними відповідних напруженостей і показують закон зміни
не змінюють своєї орієнтації. Жирні криві на рис. 7.3 є обвідними відповідних напруженостей і показують закон зміни  та
та  вздовж осі
вздовж осі 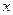 .
.
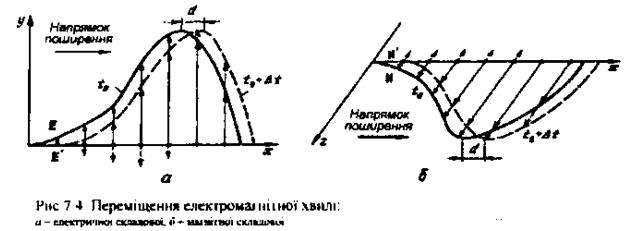 |
Оскільки електромагнітне поле змінюється за часом, розглянемо, як змінюється картина поля на рис. 7.3 в момент
 (рис. 7.4). Існуюче магнітне поле
(рис. 7.4). Існуюче магнітне поле  урезультаті зміни за часом через електромагнітну індукцію створює поле
урезультаті зміни за часом через електромагнітну індукцію створює поле  , яке орієнтоване перпендикулярно до
, яке орієнтоване перпендикулярно до  . Вектори його зображене штриховими лініями на рис. 7.4, а. Але в різних точках осі
. Вектори його зображене штриховими лініями на рис. 7.4, а. Але в різних точках осі 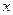 поле
поле  буде орієнтоване в різних напрямках: на зростаючій ділянці обвідної
буде орієнтоване в різних напрямках: на зростаючій ділянці обвідної  - вниз (назустріч полю
- вниз (назустріч полю  ), а на спадаючій - вверх (згідно з полем
), а на спадаючій - вверх (згідно з полем  ). У результаті взаємодії полів
). У результаті взаємодії полів  та
та  нова обвідна для моменту
нова обвідна для моменту  займе положення, зображене на рис. 7.4, а штриховою лінією. Аналогічні зміни відбудуться і з магнітним полем.
займе положення, зображене на рис. 7.4, а штриховою лінією. Аналогічні зміни відбудуться і з магнітним полем.
Як випливає з формул (7.8) та (7.7), величини виникаючих полів визначаються швидкостями зміни збуджуючих. Якщо залежності напруженостей електричного та магнітного полів однакові, то і зміни цих полів будуть такими ж. Отже, якщо обвідні полів  та
та  у момент
у момент 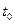 були однаковими, то і в момент
були однаковими, то і в момент  вони будуть однаковими. Має місце тільки ефект їх переміщення в напрямку осі
вони будуть однаковими. Має місце тільки ефект їх переміщення в напрямку осі 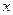 на відстань
на відстань 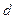 . Якщо розглянути картину полів у момент
. Якщо розглянути картину полів у момент 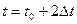 , можна встановити, що має місце переміщення їх на відстань
, можна встановити, що має місце переміщення їх на відстань  . Впродовж часу процес переміщення полів буде тривати. Отже, збудження електричного поля внаслідок зміни магнітного і збудження магнітного поля внаслідок зміни електричного призводять до того, що єдине електромагнітне поле, яке змінюється за часом, переміщується також у просторі з деякою швидкістю
. Впродовж часу процес переміщення полів буде тривати. Отже, збудження електричного поля внаслідок зміни магнітного і збудження магнітного поля внаслідок зміни електричного призводять до того, що єдине електромагнітне поле, яке змінюється за часом, переміщується також у просторі з деякою швидкістю  .
.
У фізиці процес, який залежить від координат і часу, прийнято називати хвилею. Тому розглянуте переміщення змінних за часом електричного та магнітного полів називають електромагнітною хвилею.
6.2. ПАРАМЕТРИ ТА ВЛАСТИВОСТІ ЕЛЕКТРОМАГНІТНИХ ХВИЛЬ
Швидкість поширення. Швидкість передавання енергії електромагнітною хвилею називають груповою швидкістю 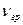 , а швидкість переміщення в просторі фази хвилі - фазовою швидкістю
, а швидкість переміщення в просторі фази хвилі - фазовою швидкістю  . Групова швидкість поширення хвилі залежить від параметрів середовища, в якому поширюється хвиля. З рівнянь Максвелла
. Групова швидкість поширення хвилі залежить від параметрів середовища, в якому поширюється хвиля. З рівнянь Максвелла
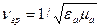 , (7.8)
, (7.8)
де 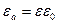 - абсолютна діелектрична проникність середовища;
- абсолютна діелектрична проникність середовища;  Ф/м - діелектрична проникність вакууму;
Ф/м - діелектрична проникність вакууму; 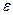 - відносна діелектрична проникність середовища;
- відносна діелектрична проникність середовища; 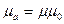 - абсолютна магнітна проникність середовища;
- абсолютна магнітна проникність середовища; 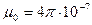 Гн/м - магнітна проникність вакууму;
Гн/м - магнітна проникність вакууму; 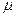 - відносна магнітна проникність середовища.
- відносна магнітна проникність середовища.
Для вакууму групова та фазова швидкості однакові
 . (7.9)
. (7.9)
Якщо підставити у формулу (7.8) значення 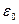 та
та 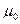 , дістаємо
, дістаємо 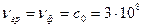 м/с, де
м/с, де 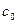 - швидкість світла у вакуумі. У будь-якому середовищі
- швидкість світла у вакуумі. У будь-якому середовищі
 . (7.10)
. (7.10)
Відносна магнітна проникність більшості середовищ, за винятком так званих феромагнітних, як це можна побачити нижче, практично дорівнює одиниці.
Date: 2016-02-19; view: 554; Нарушение авторских прав