
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Характеристики ФМ і ЧМ сигналів
|
|
| Параметри модуляції | Фазова модуляція | Частотна модуляція |
Модулюючий сигнал 
| 
| 
|
Девіація фази 
| 
| 
|
Девіація частоти 
| 
| 
|
Індекс модуляції 
| 
| 
|
Відхилення фази

| 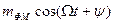
| 
|
Відхилення частоти

| 
| 
|
Спектр кутової модуляції. Сигнали з кутовою модуляцією, як і для АМ, можуть бути подані у вигляді суми гармонічних коливань. Порівняно просто це можна зробити для однотональної модуляції. Із формул (3.17) випливає, що спектри ФМ і ЧМ однакові, якщо  , тому будемо розглядати одну з них, наприклад ЧМ. Для спрощення запису надамо
, тому будемо розглядати одну з них, наприклад ЧМ. Для спрощення запису надамо  та
та  .
.
За формулою косинуса двох аргументів вираз (3.7) буде
 . (3.20)
. (3.20)
Із визначення та властивостей функцій Бесселя відомі такі співвідношення:
 ;
;
 , (3.21)
, (3.21)
 |
де
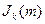 - функція Бесселя k-го порядку від аргументу т. Після підстановки виразу (3.21) у співвідношення (3.20) і виконання звичайних алгебричних перетворень та розкриття добутку тригонометричних функцій дістаємо
- функція Бесселя k-го порядку від аргументу т. Після підстановки виразу (3.21) у співвідношення (3.20) і виконання звичайних алгебричних перетворень та розкриття добутку тригонометричних функцій дістаємо
 (3.22)
(3.22)
Формулу (3.22) можна подати навіть у більш компактному вигляді, якщо врахувати, що  :
:
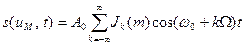 .
.
Таким чином, спектр навіть для однотональної кутової модуляції є складним. У формулі (3.22) перший член - гармонічна складова з частотою переносника, середня група гармонічних складових із частотами  є верхньою боковою смугою частот, третя група складових із частотами
є верхньою боковою смугою частот, третя група складових із частотами  представляють нижню бокову смугу частот. Число верхніх та нижніх складових теоретично нескінченне. Бокові гармонічні складові розміщені симетрично відносно частоти
представляють нижню бокову смугу частот. Число верхніх та нижніх складових теоретично нескінченне. Бокові гармонічні складові розміщені симетрично відносно частоти  на відстані
на відстані  . Амплітуди всіх складових спектра, у тому числі і на частоті переносника, пропорційні
. Амплітуди всіх складових спектра, у тому числі і на частоті переносника, пропорційні 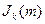 .
.
Для детального аналізу і побудови спектральних діаграм необхідно знання функцій Бесселя 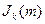 з різними значеннями
з різними значеннями  і
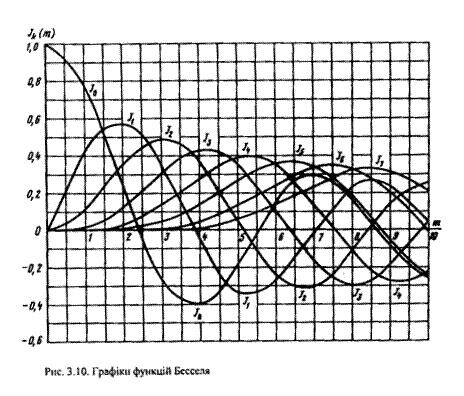
і  . Таблиці та графіки функцій Бесселя можна знайти в математичних довідниках та книгах із теорії сигналів. Для
. Таблиці та графіки функцій Бесселя можна знайти в математичних довідниках та книгах із теорії сигналів. Для  графіки функцій Бесселя зображено на рис 3.10. Значення функцій Бесселя, яких нема на рис. 3.10, можна розрахувати за рекурентною формулою
графіки функцій Бесселя зображено на рис 3.10. Значення функцій Бесселя, яких нема на рис. 3.10, можна розрахувати за рекурентною формулою
 .
.
Date: 2016-02-19; view: 484; Нарушение авторских прав