
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Виды средних и способы их вычисления
|
|
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. Он состоит из нескольких этапов:
1) устанавливается определенный показатель, т.е. обобщающий показатель совокупности, от которого зависит величина средней;
2) определяется математическое выражение для определяющего показателя;
3) производиться замена индивидуальных значений средними величинами;
4) решение уравнения средней.
Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.
Средние величины делятся на больших класса:
- степенные средние;
- структурные средние.
К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая.
В качестве структурных средних рассматриваются мода и медиана.
Степенные средние объединяются общей формулой:

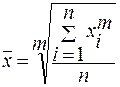 ,
,
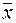 - среднее значение исследуемого явления;
- среднее значение исследуемого явления;
m – показатель степени средней;
x – текущее значение (вариант) осредняемого признака;
n – число признаков.
В зависимости от значения показателя степени m различают следующие виды средних:
При m =-1 – средняя гармоническая;
При m = 0 – средняя геометрическая;
При m = 1 – средняя арифметическая;
При m = 2 – средняя квадратическая;
При m = 3 – средняя кубическая.
При использовании одних и тех же исходных данных, чем больше m в формуле, тем больше значение средней величины:
 .
.
Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется правилом мажоритарности средних.
В зависимости от представления исходных данных степенные средние могут быть простыми и взвешенными. Простая средняя рассчитывается по не сгруппированным данным и имеет следующий вид:
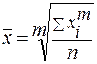 .
.
Взвешенная средняя считается по сгруппированным данным и имеет общий вид:
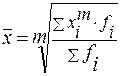
где xi - значение (варианта) осредняемого признака;
m – показатель степени средней;
fi - частота (вес), показывающая сколько раз встречается i – е значение осредняемого признака.
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объём признака в совокупности сохраняется неизменным. Средняя арифметическая применяется в форме простой средней и взвешенной средней.
Средняя арифметическая простая равна сумме отдельных значений осредняемого признака, деленной на общее число этих значений:

Она применяется в тех случаях, когда имеются не сгруппированные индивидуальные значения признака.
Средняя арифметическая взвешенная вычисляется по формуле:
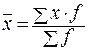
Она применяется в тех случаях, когда известны варианты, имеющие неравновеликие частоты (f).
Технику вычисления средней арифметической величины рассмотрим на примере расчета среднего возраста студентов в группе из 20 человек.
| № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) |
Средний возраст рассчитывается по формуле по формуле простой средней:

Сгруппируем исходные данные. Получим ряд распределения:
| Возраст, x лет | Всего | |||||
| Число студентов, f |
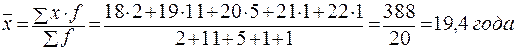
Средняя гармоническая – это величина обратная среднеарифметической.
В тех случаях, когда вес каждого варианта равен единице, применяется средняя гармоническая простая, исчисляемая по формуле:
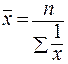
Когда статистическая информация не содержит частот f по отдельным вариантам x совокупности, а представлена как их произведение x*f, применяется формула средней гармонической взвешенной.
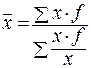
Средняя геометрическая применяется в тех случаях, когда необходимо сохранить неизменным произвдениее индивидуальных величин.
Средняя геометрическая простая имеет следующий вид:
 где
где  - знак произведения, n – число вариантов, периодов.
- знак произведения, n – число вариантов, периодов.
Средняя геометрическая взвешенная имеет следующий вид:

Средняя квадратическая применяется, когда необходимо рассчитать средний размер признака, выраженный в квадратных единицах измерения.
Средняя квадратическая простая имеет вид:
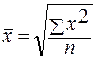
Средняя квадратическая взвешенная имеет вид:
 .
.
Средняя кубическая применяется, когда необходимо рассчитать средний размер признака, выраженный в кубических единицах измерения.
Средняя кубическая простая имеет вид:
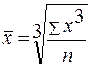 .
.
Средняя кубическая взвешенная имеет вид:
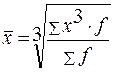 .
.
Рассмотрим структурные средние.
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода Мо наиболее часто встречаемое значение признака.
В дискретном вариационном ряду – вариант, имеющий наибольшую частоту.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
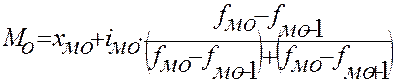 ,
,
где xмо - начало модального интервала; модальный интервал определяется по наибольшей частоте.
iмо - модальный интервал;
fмо fмо-1 fмо+1 - частота модального, до и послемодального интервалов соответственно.
В случае неравных интервалов применяется следующая формула:
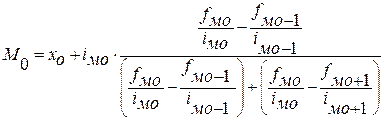
где xмо - начало модального интервала, модальный интервал – интервал, в котором достигает максимума величина  (плотность) – отношение частоты интервала к его величине;
(плотность) – отношение частоты интервала к его величине;
iмо, iмо-1, iмо+1 - величина соответственно модального, до и послемодального интервалов.
Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т. п.
Медиана Ме – величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части, т. е. со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находиться в середине упорядоченного ряда.
Для определения медианы в вариационном ряду необходимо вначале найти номер медианы: 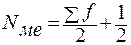 .
.
Затем используют накопленные частоты (сумму последовательно сложенных частот между собой).
В дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В интервальных рядах распределения медианное значение рассчитывается по формуле:
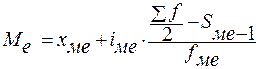
где xме - нижняя граница медианного интервала; медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.
iме - медианный интервал;
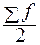 - половина от общего числа наблюдений;
- половина от общего числа наблюдений;
Sме-1 - сумма наблюдений, накопленная до начала медианного интервала;
fме - число наблюдений в медианном интервале.
Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значения имеют какой-либо конкретный вариант в вариационном ряду.
Рассмотрим на примерах расчет моды и медианы.
Пример 1.
Распределение семей города по числу детей характеризуется следующими данными:
| Число детей в семье | Итого | ||||||
| Число семей |
Определить моду и медиану.
Наибольшая частота (29 изделий) приходится на семью с 2 детьми. Следовательно, Мо = 2.
Для определения медианы нужно вначале найти номер медианы:
Nме =  =
= 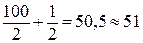
Затем используют накопленные частоты.
Накапливаем частоты до тех пор, пока накопленная частота не будет равна этому номеру или превысит его.
| Число детей в семье | Итого | ||||||
| Число семей | |||||||
| Накопленная частота | - |
Следовательно, 10 семей не имеют детей, 36 (10+26) семей имеют не более 1 ребенка, 65 (36+29) не более 2 детей, 82 (65+17) не более 3 детей и т. д. Т. о, медиана данного ряда распределения равна 2 детям в семье, т. е. половина семей имеют до 2 детей, а другая свыше 2-х детей.
Ме = 4 балла.
Пример 2.
Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:
| Длина пробега за 1 рейс, км. | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80 и выше | Итого |
| Число рейсов за 1 месяц |
Определите модальное и медианное значение длины пробега за 1 рейс.
Модальным в данном распределении является интервал 40-50 км., так как наибольшее число рейсов (f = 25) находится в этом интервале.
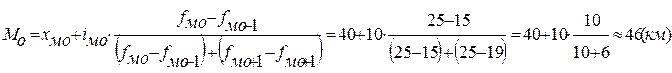
Определим медианный интервал:
Nме =  =
= 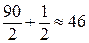
Затем используют накопленные частоты.
| Длина пробега за 1 рейс, км. | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80 и выше | Итого |
| Число рейсов за 1 месяц | |||||||
| Накопленная частота | - |
Медианным считается интервал 50-60 км., так как в этом интервале находятся номер медианы.
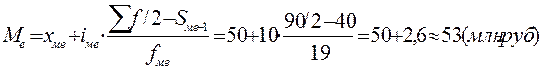
Половина рейсов за месяц были протяженностью до 53 км., а другая половина свыше 53 км.
Date: 2016-02-19; view: 504; Нарушение авторских прав