Распространение выборочных результатов на генеральную совокупность

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе выборочных результатов.

Выборочные средние и относительные величины распространяют на генеральную совокупность с учетом предела их возможной ошибки.

В каждой конкретной выборке расхождение между выборочной средней и генеральной, т. е может быть меньше средней ошибки m, равно ей или больше её.

Причем каждое из этих расхождений имеет различную вероятность (объективную возможность появления события). Поэтому фактические расхождения выборочной средней и генеральной можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью p.

Предельную ошибку выборки для средней () при повторном отборе можно рассчитать по формуле:

,

t - где нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;

- средняя ошибка выборки.

Аналогичным образом может быть записана формула предельной ошибки выборки для доли D_w при повторном отборе

D_w = t* .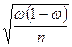

При случайном бесповторном отборе в формулах расчета предельных ошибок выборки необходимо умножить подкоренное выражение на (1- ):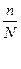

Для количественного признака

D_x = t* m 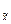= t * ,

для доли

D_w = t* m_w = t* .

Формула предельной ошибки вытекает из основных положений теории выборочного метода, сформулированных в ряде теорем теории вероятностей, отражающих закон больших чисел.

На основании теоремы П. Л. Чебышева (с уточнением А. М. Ляпунова) с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объёме выборки и ограниченной генеральной дисперсии выборочные показатели (средняя, доля) будут сколь угодно мало отличаться от соответствующих генеральных показателей.

Применительно к нахождению среднего значения признака эта теорема может быть записана так:

P [ ] = Ф (t),

А для доли признака

P [ ] = Ф (t),

Где генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности):

Ф (t) =

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью. З значения функции Ф (t) при различных значениях t как коэффициент кратности средней ошибки выборки, специально составленных таблиц. Приведем некоторые значения, применяемые наиболее часто для выборок достаточно большого объёма (n ):

T 1,000 1,960 2,000 2,580 3,000

Ф (t) 0,683 0,950 0,954 0,990 0,997

Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется вероятностью, значение которой определяется коэффициентом t (в практических расчетах, как правило, заданная вероятность не должна менее 0,95). Так при t = 1 предельная ошибка составит D = m. Следовательно, с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы 1m. При t = 2 с вероятностью 0,954 она не выйдет за пределы 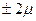, при t = 3 с вероятностью 0,997 – за пределы и т. д.

Выборочное наблюдение проводиться в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) генеральной совокупности.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

для средней

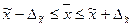
для доли p = w ± D_w w-D_w

Это означает, что с заданной вероятностью можно утверждать, что значения генеральной средней следует ожидать в пределах от до .

Аналогичным образом может быть записан доверительный интервал генеральной доли ; .

Наряду с абсолютным значением предельной ошибки выборки рассчитывается и предельная относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:

для средней, %: D_% = *100;

для доли, %: D_% = *100.

Date: 2016-02-19; view: 424; Нарушение авторских прав