Зенитально-азимутальные

Из наблюдения одной звезды получают Z и A, а затем находят координаты точки Z (линейно-угловая засечка). Но поскольку светила постоянно движутся, то одновременно наблюдать Z и A сложно, поэтому такая методика редко применяется на практике.

Известно, что географическая долгота пункта относительно начального меридиана численно равна разности одноименных местных времен, определенных одновременно как в пункте наблюдения, так и в пункте, расположенном на начальном меридиане, т. е.

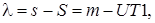(1.31)

где S – звездное время на Гринвиче в момент наблюдения Т;

UT 1 – всемирное время в момент наблюдения Т.

Момент времени Т фиксируется по хронометрам, которые могут идти неправильно. Поэтому возникает задача определения поправки хронометра U. Зная поправку, можно записать

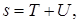(1.32)

где T – показание хронометра, приближенно определяющее звездное время; U – поправка хронометра.

Итак, для определения широты j и долготы l в точке наблюдений, необходимо измерять: Z, A, T, а также знать поправку хронометра.

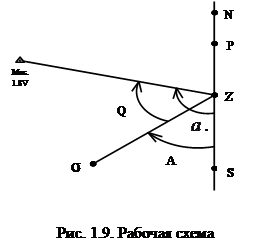
Задача определения азимута направления на земной предмет сводится обычно к определению азимута светила A и измерению горизонтального угла Q между светилом и местным предметом (см. рис. 1.9). В этом случае азимут направления на земной предмет определяется формулой

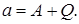(1.33)

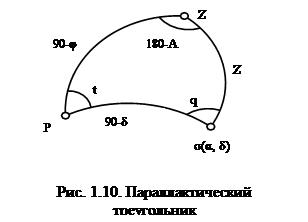
Аналитическое обоснование различных способов определения широты, времени и азимута вытекает из решения параллактического треугольника PZs (см. рис. 1.10), построенного для каждого наблюдаемого светила.

Параллактическим треугольником называется сферический треугольник, у которого вершинами являются зенит места наблюдения, полюс мира и светило (см. рис. 1.10). Три его стороны являются дугами больших кругов:

È PZ = 90 – j; È Z s = Z; È P s = D = 90° – d.

Сферические углы: t – часовой угол; 180° – А, где А – азимут светила; q – параллактический угол.

В этой группе способов основным уравнением, вытекающим из параллактического треугольника PZ s и связывающим измеренную величину Z в некоторый момент T с определяемыми значениями широты j и времени S, является известное уравнение связи.

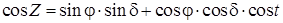, (1.34)

где t = s – a = T + U – a.

Полагая, что Z и T известны из измерений, а значения экваториальных координат a и d выбираются из AE на момент наблюдений, уравнение (1.34) будет иметь два неизвестных: j и U [12].

Чтобы найти неизвестные, необходимо выполнить наблюдения не менее двух звезд или наблюдения одного и того же светила не менее двух раз.

Определение j и U может быть выполнено как совместно, так и раздельно. Рассмотрим способы определения j и U.

Раздельный способ

Наблюдаем светило в плоскости меридиана, тогда t = 0, а значит основное уравнение (1.34) примет вид

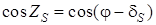, (1.35)

Так как cos t = 1, следовательно, можно записать

Z_S = j – d _S или j = Z_S + d _S, (1.36)

Зная j, будем иметь в уравнении (1.34) лишь одно неизвестное U. Для его определения нужно отнаблюдать звезду в момент T. Зная U, находим местное звездное время s = T + U и, затем, долготу l = s + S [6].

Способ совместного определения

Необходимо измерить зенитные расстояния минимум двух светил, расположенных в произвольных, но взаимно перпендикулярных вертикалах.

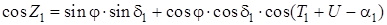
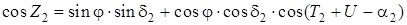, (1.37)

Но зенитные расстояния измеряются не точно, особенно с увеличением широты. Поэтому рекомендуется наблюдать звезды на одном круге высот (альмукантарате).

В этом случае Z ₁ = Z ₂, поэтому

.

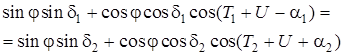
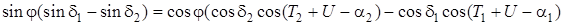Тогда j найдем по формуле

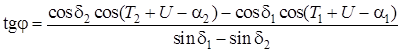. (1.38)

Преимущества данного способа:

1. Не надо измерять Z, нужно только фиксировать момент прохождения звезд через горизонтальную нить не изменяя наклон зрительной трубы. Таким образом, исключаются ошибки отсчитывания по вертикальному кругу.

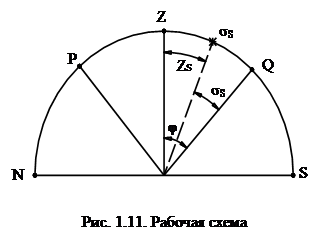
2. Измененными величинами являются только моменты T₁, T₂ прохождения звезд через изображенный альмуканторат (см. рис. 1.11).

Единственным недостатком данного способа является то, что неизвестные j и U находятся под знаками тригонометрических формул, т. е. уравнение нелинейно. Для повышения точности необходимо исходное уравнение (1.34) привести к линейному виду и отыскивать поправки Dj и D U из обработки многократных наблюдений

.

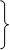
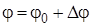
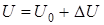Date: 2015-06-05; view: 766; Нарушение авторских прав