Основные формулы связи различных времен

Звездное время S, истинное солнечное время m _¤ и среднее солнечное время m в какой-либо точке земной поверхности называются соответственно местным звездным, местным истинным солнечным и местным среднем солнечным временем этой точки [3].

На одном и том же меридиане Земли время будет одинаковым, на разных меридианах – различным. Местное время на меридиане Гринвича обозначается большими буквами:

S – гринвичское звездное время;

М _¤ – гринвичское истинное солнечное время;

М – гринвичское среднее солнечное время, называемое всемирным временем.

В Астрономическом Ежегоднике на каждую дату публикуется звездное время на Гринвиче (S ₀), когда М = 0 ^h.

Найдем, чему равна разность одноименных местных времен, определенных в один и тот же физический момент в двух пунктах А и В земной поверхности, расположенных на разных географических меридианах.

Предположим, что точка В лежит на Гринвиче (l_B = 0^h), тогда справедливы следующие равенства

s = S + l;

m _¤ = M _¤ + l; (1.16)

m = M + l.

Из формул (1.16) следует, что географическая долгота пункта от Гринвича (в часовой мере) равна разности местного и гринвичского времени. Данные формулы дают принципиальную основу для определения долгот пунктов от Гринвича.

Из многочисленных астрономических наблюдений установлено, что в течение года Солнце проходит через меридиан на один раз меньше, чем точка весеннего равноденствия. Отсюда следует, что в году число средних суток на единицу меньше, чем звездных, т. е.

1 средние сутки = 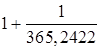звездных суток,

или 1 средние сутки = (1 + m) звездных суток,

где .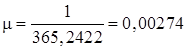

Переходя от суток к единицам времени, получим s = m (1 + m).

Определим формулу для перехода от среднего солнечного времени m к звездному s, учитывая тот факт, что звездные и средние солнечные сутки начинаются не в один и тот же момент.

Тогда формула будет иметь вид:

s = s ₀ + m (1 + m), (1.17)

где s ₀ – местное звездное время в местную среднюю полночь местного среднего солнечного времени.

Применительно к Гринвичу формула (1.17) будет такой

S = S ₀ + M (1 + m). (1.18)

Установим связь между s ₀ и S ₀. Для этого найдем разность выражений (1.17) и (1.18).

s – S = s ₀ + m (1 + m) – S ₀ – M (1 + m),

и, выполнив ряд преобразований, получим

s ₀ = S ₀ – m×l. (1.19)

Формулы (1.17) и (1.18) позволяют получить по m значение s. Обратный переход от s к m выполняется в соответствии с (1.17) по формуле

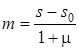. (1.20)

При международных отношениях для публикации большинства астрономических явлений в астрономических ежегодниках, а также во многих научных исследованиях широко используется всемирное время. Однако введение всемирного времени на всем земном шаре для целей повседневной жизни вызвало бы противоречие с самой природой, так как на меридианах, удаленных от гринвичского на значительные расстояния, часы дня не соответствовали бы положению Солнца над горизонтом.

Поэтому в 1884 году была предложена поясная система счета среднего времени.

При поясном счете времени весь земной шар мысленно разделен географическими меридианами через 15º по долготе на 24 часовых пояса. Счет осевых меридианов начинается от гринвичского меридиана, являющегося в то же время осевым меридианом нулевого часового пояса. При пересечении границ часовых поясов поясное время меняется ровно на один час.

При таком счете времени за начало суток принимается полночь осевого меридиана данного пояса. Если обозначить поясное время, соответствующее часовому поясу с номером n, через T_n, а нулевому поясу – через M (всемирное время), то очевидно, что

T_n = M + n. (1.21)

В 1930 году Советским Правительством был издан декрет, согласно которому по экономическим соображениям стрелки часов были переведены ровно на один час вперед по сравнению с поясным временем. Такое время, получившее название декретного времени сохраняется в РБ, как и в некоторых других странах, до сих пор.

Декретное время D связано с поясным временем T следующим соотношением

D = T_n + k, (1.22)

где k – добавка к поясному времени, установленная декретом. С 1991 года в РБ зимой k = 0^h, летом k = 1^h.

По декретному времени идут бытовые часы.

Декретное время связано с мировым временем:

D = M + (n + k), (1.23)

со среднем солнечным временем

D = m – l + n + k, (1.24)

с истинным солнечным временем

D = m₀ – h – l + n + k. (1.25)

Формулы (1.16), (1.17), (1.19), (1.20), (1.23) – (1.25) позволяют решать различные задачи по расчету времени.

Date: 2015-06-05; view: 1068; Нарушение авторских прав