Пример. Автобусы некоторого маршрута идут с интервалом 5 минут

Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.

Решение. Время ожидания является случайной величиной, равномерно распределенной в интервале [0,5]. Тогда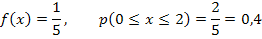

Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:

(6.2)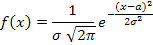

Замечание. Таким образом, нормальное распределение определяется двумя параметрами: а и s.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Выясним, какой вид имеет эта кривая, для чего исследуем функцию (6.1).

1. Область определения этой функции: (-¥, +¥).

2. f (x) > 0 при любом х (следовательно, весь график расположен выше оси Ох).

3. то есть ось Ох служит горизонтальной асимптотой графика при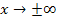

4. 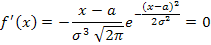при х = а; f' (x) > 0 при x > a, f' (x) < 0 при x < a. Следовательно, — точка максимума.

5. F (x – a) = f (a – x), то есть график симметричен относительно прямой х = а.

6. 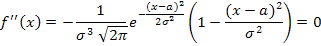при x = a ± s, то есть точки являются точками перегиба.

Примерный вид кривой Гаусса изображен на (рис. 6.1).

Рис. 6.1. Кривая Гауса

Найдем вид функции распределения для нормального закона:

(6.3)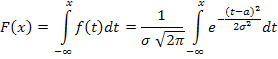

Перед нами так называемый «неберущийся» интеграл, который невозможно выразить через элементарные функции. Поэтому для вычисления значений F (x) приходится пользоваться таблицами. Они составлены для случая, когда а = 0, а s = 1.

Нормальное распределение с параметрами а = 0, s = 1 называется нормированным, а его функция распределения

(6.4)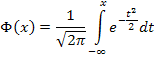

— функцией Лапласа.

Замечание. Функцию распределения для произвольных параметров можно выразить через функцию Лапласа, если сделать замену: , тогда .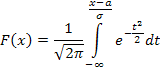

Найдем вероятность попадания нормально распределенной случайной величины на заданный интервал:

(6.5)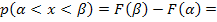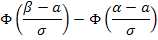

Date: 2015-06-05; view: 2799; Нарушение авторских прав