Пример. Рассмотрим игру в преферанс, когда старшие 32 карты карточной колоды случайным образом распределяются (сдаются) между тремя игроками

Рассмотрим игру в преферанс, когда старшие 32 карты карточной колоды случайным образом распределяются (сдаются) между тремя игроками, получающими по 10 карт, и «прикупом», куда кладутся две карты. Какова вероятность того, что в «прикупе» окажутся два «туза»?

Число различных комбинаций из двух карт, которые могут оказаться в «прикупе», равно числу сочетаний из 32 по 2, что составляет 32! / (2! 30!) = 496. В карточной колоде имеется ровно четыре «туза» и число различных комбинаций, дающих два «туза», равно числу сочетаний из 4 по 2, что составляет 4! / (2! 2!) = 6. Следовательно, искомая вероятность есть

С ²₄ / С ²₃₂ = 6 / 496» 0,012

Предположим, что один из игроков — «играющий» — имеет пять старших карт одной масти (скажем, «червей»), исключая «даму». При объявлении ранга игры, «играющему» приходится учитывать возможность образования у одного из противников — «вистующих» — комбинации из трех оставшихся «червей» (так называемую «третью даму»). Какова вероятность этого события?

Всего имеется С ¹⁰₂₀ = 20! / (10! 10!)

равновероятных случаев распределения 20 карт на две равные группы по 10 карт, которые «сдаются» каждому из двух игроков. Если всю комбинацию «третья дама червей» зафиксировать у какого-либо определённого игрока, то число совместимых с этим случаев распределения равно числу сочетаний из 17 оставшихся карт по 7. следовательно, вероятность образования у вполне определенного противника «третьей дамы червей» есть

С ⁷₁₇ / С ¹⁰₂₀ = 8 ´ 9 ´ 10 / (18 ´ 19 ´ 20)» 0,12

3. Во всех приведенных выше формулах встречается выражение n! = 1.2... (n - 1) n. Существует сравнительно простое асимптотическое соотношение, называемое формулой Стирлинга при больших n

(5.7)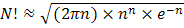

Date: 2015-06-05; view: 4436; Нарушение авторских прав