Пример. Пусть события А1, , An независимы и имеют каждое вероятность р

Пусть события А ₁,..., A_n независимы и имеют каждое вероятность р. Эти события можно интерпретировать как «успехи» в наблюдении некоторого случайного события в n независимых испытаниях. Тогда вероятность наступления ровно m успехов равна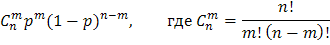

Действительно, можно взять W = {(i ₁..., i_n), все i_k = 0 или 1}, где i_k = 1 соответствует наступлению А_k, а i_k = 0 — его ненаступлению. Наступлению m успехов благоприятствуют те исходы (i ₁,..., i_n), у которых среди i_k ровно m единиц; всего таких исходов C_n^m, а вероятность каждого такого исхода в силу независимости A_k, равна p^m (1 - p) ^{m - n}.

К этому примеру непосредственно примыкает одна из первых (и важнейших) предельных теорем теории вероятностей — теорема Бернулли (простейшая форма больших чисел закона), согласно которой вероятность значит. уклонения частоты успехов n от вероятности р при больших n становится сколь угодно малой. Таким образом, рассматриваемая математическая модель случайных явлений приводит к согласующемуся с практическими наблюдениями выводу о стабилизации частот случайных событий около их вероятностей.

Скорость стремления частоты n к p оценивают с помощью теоремы Лапласа (частный случай центральной предельной теоремы). С ростом n вероятность

стремится к Ф(b) - Ф(а), где — .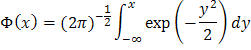

Вопросы для самопроверки

1. Что такое априорная вероятность?

2. Дайте определение апостериорным вероятностям.

3. Напишите формулу полной вероятности.

4. Напишите формулу Байеса.

5. Дайте определение гипотезе.

6. Что называют суммой событий?

7. Что называют произведением событий?

8. Что называют разностью событий?

9. Сформулируйте теорему умножения вероятностей.

Date: 2015-06-05; view: 743; Нарушение авторских прав