Теорема Эйлера

Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны. Обозначим n_k — число вершин, имеющих степень k, k = 0, 1, 2,.... Известно, что:

(2.2)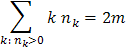

Для ориентированных графов для каждой вершины можно ввести два числа — полустепень исхода d_i ⁺ (число выходящих из нее вершин) и полустепень захода — d_i ^- (число входящих в нее вершин). В дальнейшем, будем рассматривать графы без петель, то есть без дуг, у которых начальная и конечная вершины совпадают. Известно, что:

(2.3)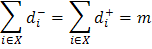

для эйлерова графа имеет место: d_i ⁺ = d_i ^- i = 1,2, …, n; эйлеров граф является объединением контуров, попарно не имеющих общих ребер.

Матрица смежности графа — квадратная матриц n ´ n, элемент a_ij которой равен единице, если (i, j) Î V, и нулю, если (i, j) Ï V, i, j Î X.

Для неориентированного графа матрица смежности всегда симметрическая.

Матрица инциденций для ребер графа это прямоугольная матрица n ´ m, элемент r_ij которой равен единице, если вершина i инцидентна ребру j, и нулю в противном случае, i = 1,2, …, n, j = 1,2, …, m.

Матрица инциденций для дуг графа — это прямоугольная матрица m ´ n, элемент r_ij которой равен плюс единице, если дуга U_j исходит из вершины i, минус единице, если дуга U_j заходит в вершину i, и нулю в остальных случаях, i = 1,2, …, n, j = 1,2, …, m.

Деревом называется связный граф без простых циклов, имеющий не менее двух вершин. Для дерева m = n – 1, а число висячих вершин равно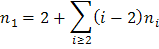

Можно доказать, что в дереве любые две вершины связаны единственной цепью.

Прадеревом называется ориентированное дерево, у которого одна из вершин, называемая корнем, не имеет заходящих дуг, а степени захода остальных вершин равны единице.

Плоским (планарным) называется граф, который можно изобразить на плоскости так, что различным вершинам соответствуют различные кружки и никакие два ребра не имеют общих точек, отличных от их границ (не пересекаются).

Для плоского графа существует понятие грани — части плоскости, ограниченной ребрами и не содержащей внутри себя ни вершин, ни ребер. Для простоты определения грани в дальнейшем в основном будем рассматривать графы без висячих вершин. Например, дерево имеет всего одну внешнюю грань — всю плоскость.

Степенью грани называется число ее граничных ребер (висячие ребра считаются дважды).

Обозначим p — число граней плоского графа, p_k — число его граней, имеющих степень k, q_i — степень i -ой грани.

Date: 2015-06-05; view: 528; Нарушение авторских прав