Элементы теории графов

Теория графов в качестве теоретической дисциплины может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.

Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.

Задача настоящего материала изложить основные понятия и результаты теории графов.

Основные понятия теории графов

Свое начало теория графов берет с решения Л. Эйлером популярной в 18 веке (1736 г.) «задачу о кенигсбергских мостах: необходимо было пройти по всем мостам Кенигсберга попадая на каждый мост один раз.

Термин «граф» впервые был введен в 1936 г. Д. Кенигом.

Граф — это система, которая может быть представлена как множество кружков и множество соединяющих их линий (рис. 2.1).

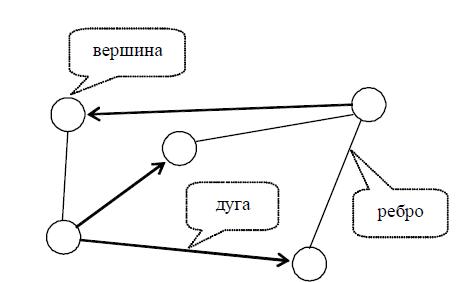
Рис. 2.1. Геометрический способ задания графа

Кружки называются вершинами графа, линии со стрелками — дугами, без стрелок — ребрами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным; граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным.

Теория графов может рассматриваться как раздел теории множеств или раздел дискретной математики.

Граф это конечное множество X, состоящее из n элементов (X = {1, 2,..., n }), называемых вершинами графа, и подмножество V декартова произведения X ´ X, то есть V Í X 2, называемое множеством дуг.

Ориентированным графом G называется совокупность (X, V).

Неориентированным графом называется совокупность множества X и множества неупорядоченных пар элементов, каждый из которых принадлежит множеству X).

Дугу между вершинами i и j; i, j Î X, будем обозначать (i, j). Число дуг графа будем обозначать m (V = (v ₁, v ₂,..., v_m)).

Язык графов является удобным способом для описания многих физических, технических, экономических, биологических, социальных и других систем.

Подграфом называется часть графа, образованная подмножеством вершин вместе со всеми ребрами (дугами), соединяющими вершины из этого множества. Если из графа удалить часть ребер (дуг), то получим частичный граф.

Определение. Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) — инцидентным соответствующим вершинам.

Определение. Путем называется последовательность дуг (в ориентированном графе), такая, что конец одной дуги является началом другой дуги.

Простой путь — путь, в котором ни одна дуга не встречается дважды. Элементарный путь — путь, в котором ни одна вершина не встречается дважды.

Контур — путь, у которого конечная вершина совпадает с начальной вершиной. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).

Граф, для которого из (i, j) Î V следует (j, i) Î V называется симметрическим.

Если из (i, j) Î V следует, что (j, i) Ï V, то соответствующий граф называется антисимметрическим.

Цепью называется множество ребер (в неориентированном графе), которые можно расположить так, что конец (в этом расположении) одного ребра является началом другого. Другое определение: цепь — последовательность смежных вершин.

Замкнутая цепь называется циклом.

По аналогии с простым и элементарным путем, можно определить соответственно простые и элементарные цепь и цикл. Любой элементарный цикл является простым, обратное утверждение в общем случае неверно.

Элементарная цепь (цикл, путь, контур), проходящая через все вершины графа называется гамильтоновой цепью (соответственно — циклом, путем, контуром).

Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа называется эйлеровой цепью (соответственно — циклом, путем, контуром).

Если любые две вершины графа можно соединить цепью, то граф называется связным. Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами.

Связностью графа называется минимальное число ребер, после удаления которых граф становится несвязным.

Для ориентированных графов, если любые две вершины графа можно соединить путем, то граф называется сильно связным. Известно, что: связность графа не может быть больше, чем [2 m / n ], где [ x ] — целая часть числа x; существуют графы с n вершинами и m ребрами, имеющие связность [2 m / n ]; в сильно связном графе через любые две вершины проходит контур.

Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом.

В неориентированном графе степенью вершины i называется число d_i инцидентных ей ребер. Очевидно, d_i £ n – 1, i Î X.

Граф, степени всех вершин которого равны n – 1, называется полным.

Граф, все степени вершин которого равны, называется однородным.

Вершина, для которой не существует инцидентных ей ребер (d_i = 0) называется изолированной.

Вершина, для которой существует только одно инцидентное ей ребро (d_i = 1) называется висячей.

Известно, что: в любом графе число вершин нечетной степени четно.

Date: 2015-06-05; view: 1506; Нарушение авторских прав