Пример. Пусть Х — множество всех действительных чисел; если для каждого х Î Х положить у = f(x) = arctg х

Пусть Х — множество всех действительных чисел; если для каждого х Î Х положить у = f (x) = arctg х, то этим будет установлено отображение множества Х на интервал (-p / 2, p / 2).

(1—1)-соответствие между двумя множествами Х и Y есть такое отображение множества Х в множество Y, при котором каждый элемент множества Y является образом одного и только одного элемента множества X. Отображения примеров 2) и 3) взаимно однозначны, примера 1) — нет.

Операции над множествами. Диаграммы Эйлера-Венна

Суммой, или объединением, двух, трёх, вообще произвольного конечного или бесконечного множества множеств называется множество всех тех предметов, каждый из которых есть элемент хотя бы одного из данных множеств-слагаемых.

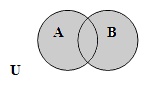
	A È B = { x | x Î A или x Î B }

Пересечением двух, трёх, вообще любого конечного или бесконечного множества множеств называется множество всех элементов, общих всем данным множествам. Пересечение даже двух непустых множеств может быть пустым.

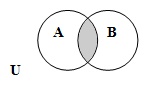
	A Ç B = { x | x Î A и x Î B }

Разностью между множеством В и множеством А называется множество всех элементов из В, не являющихся элементами из А: разность между множеством В и его частью А называется дополнением множества А в множестве В.

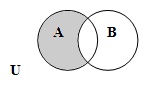
	A \ B = { x | x Î A или x Ï B }

Симметрическая разность двух заданных множеств A и B — это такое множество A D B, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество:

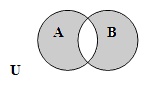
	A D B = { x | x Î A \ B и x Î B \ A }

Упорядоченные множества. Установить в данном множестве Х порядок — значит установить для некоторых пар x', х" элементов этого множества какое-то правило предшествования (следования), выражаемое словами "элемент x' предшествует элементу х", x' < х"", или, что то же, "элемент x' следует за элементом х", x' < х"", причём предполагается выполненным условие транзитивности: если х < x' и x' < х", то х < х". Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком, называется «частично упорядоченным множеством»; иногда вместо «частично упорядоченное множество» говорят «упорядоченное множество». Однако чаще упорядоченным множеством называется такое частично упорядоченное множество, в котором порядок удовлетворяет следующим дополнительным требованиям («линейного порядка»):

1. никакой элемент не предшествует самому себе;

2. из всяких двух различных элементов х, x' один предшествует другому, т.е. или х < x', или x' < х.

Date: 2015-06-05; view: 680; Нарушение авторских прав