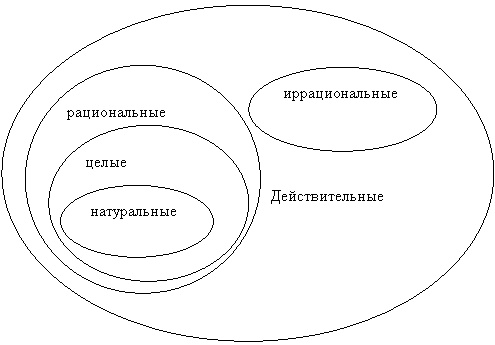
Множество целых, рациональных и иррациональных чисел

Множество всех чисел, противоположных натуральным, называется множеством целых отрицательных чисел. Сами натуральные числа при этом называют целыми положительными числами. Множество целых отрицательных чисел, множество целых положительных чисел и число нуль вместе называются множеством целых чисел.

Это множество обозначается Z = {…, -2, -1, 0, 1, 2, …}.Сами натуральные числа иногда записывают со знаком плюс (+) Z₊, а им противоположные пишут со знаком минус (–) Z _-. Знак минус перед целым отрицательным числом называется знаком количества в отличие от знака вычитания, который называется знаком действия.

Результаты сложения, вычитания и умножения целых чисел являются целыми числами, а Результат деления целых чисел не всегда является целым числом.

Множество рациональных чисел:

(2.1)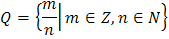
где	m — целое число; n — натуральное число.

Рациональные числа — это числа, представимые в виде дроби . Все натуральные и целые числа — рациональные. Т.е. Множество целых чисел и множество натуральных чисел являются подмножествами множества рациональных чисел. Пример рационального множества можно привести: .

Множество иррациональных чисел это множество чисел, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел — .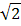

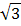
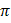Множество действительных (вещественных) чисел: это объединение множества рациональных чисел и множества иррациональных чисел. Обозначается.

R = { a ₀, a ₁, a ₂, a ₃, a ₄, a ₅,… a ₀ Î Z, a_k Î {0,1,2,3,4,5,6,7,8,9}}.

Любое действительное число можно отобразить на числовой прямой:

Для перечисленных выше множеств чисел справедливо следующее высказывание:

N Ì Z Ì Q Ì R

Числовой осью называется прямая, на которой изображаются действительные числа. Для превращения прямой в числовую ось необходимо:

· выбрать положительное направление — одно из двух возможных на прямой (обычно слева-направо);

· выбрать начало отсчёта О и точку А — конец единичного отрезка (единицу масштаба).

Тогда всякое действительное число будет изображаться точкой числовой оси по следующим правилам. Число 0 изображается точкой О, число а — точкой А. Если число x положительно, оно изображается точкой В, такой что она находится по ту же сторону от точки О, что и точка А. Если же число х отрицательно, оно изображается такой точкой С, которая находится по разные стороны от точки О с точкой А. Такое соответствие между множеством точек прямой и множеством действительных чисел взаимно однозначно. Поэтому часто понятия «точка числовой прямой» и «действительное число» не различаются, в частности, оба вышеупомянутых множества обозначаются одной и той же буквой R.

На нашей модели числовой прямой расстояние от точки, изображающей число а, до начала отсчёта равно | a | — модулю (абсолютной величине) числа а; расстояние между числами а и b (точками на числовой оси) равно | a – b |. Середина отрезка с концами а и b занята числом .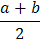

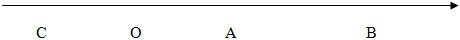
Date: 2015-06-05; view: 4060; Нарушение авторских прав