Тема работы № 6. Определения по результатам ротационной вискозиметрии коэффициента динамической вязкости ньютоновской жидкости

Цель:

Ознакомиться с работой ротационного вискозиметра

Задачи:

Вывести формулу для определения вязкости ньютоновской жидкости;

Рассчитать коэффициент динамической вязкостью по формуле Маргулеса.

Ход работы:

Рассмотрим подробно теорию ротационных вискозиметров, поскольку в инструкциях приборов, как правило, не приводятся математические выкладки, из-за чего не всегда ясно, какие сделаны при выводе расчетных формул допущения, а в справочной литературе нередки опечатки. Кроме того, данное учебное пособие предусматривается как литература для учебных занятий, поэтому в нем нецелесообразно приводить конечные формулы с отсылкой на какую-либо справочную литературу.

Для конкретности рассмотрим схему ротационного вискозиметра типа немецкого вискозиметра «Реотест», в котором внешний цилиндр неподвижен, а внутренний вращается (на нем измеряются крутящий момент и угловая скорость). Схема прибора показана на рис. 2.6. Течение полагаем стационарным, ламинарным, изотермическим. Компоненты скорости течения вдоль продольной оси цилиндров и в направлении радиуса полагаем равными нулю. Следовательно, реологические эффекты второго порядка: эффекты Вейссенберга, Пойнтинга, вихри Тейлора – в рамках данной теории не описываются.

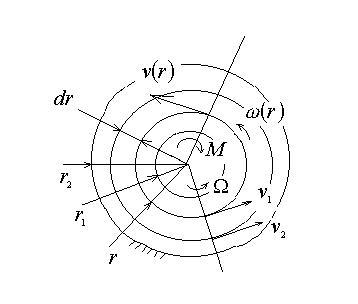
Рис.1. Расчетная схема ротационного вискозиметра

Запишем уравнение равновесия в моментах относительно оси вращения мысленно выделенного цилиндрического осесимметричного элемента вискозиметра с ротором и слоем жидкости, на который действуют активный момент на роторе и реактивный момент от сил вязкого трения на внешней поверхности цилиндра жидкости:

2p r ² L t – M_L = 0, (1)

где r – текущий радиус; L – длина цилиндров; t – касательное напряжение на поверхности цилиндра жидкости с радиусом r; M_L – крутящий момент, активный момент.

Тогда

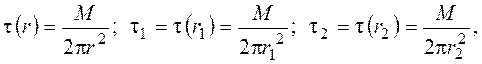(2)

где 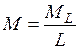– крутящий момент на единицу длины цилиндров; t₁, t₂ – касательное напряжение на рабочих поверхностях внутреннего и наружного цилиндров; r ₁– наружный радиус внутреннего цилиндра (ротора); r ₂ – внутренний радиус неподвижного наружного цилиндра.

Такой же результат можно получить из уравнений движения в цилиндрических координатах. Из кинематических соображений запишем скорость сдвига в жидкости в цилиндрических координатах:

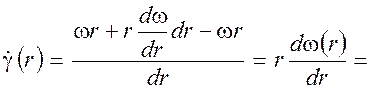
, (3)

где 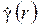– скорость сдвига на поверхности цилиндра жидкости с текущим радиусом; w (r) – угловая скорость цилиндра жидкости с текущим радиусом; v (r) – линейная скорость точек цилиндра жидкости с текущим радиусом.

Реологическое уравнение жидкости с учетом выражений (2) можно записать следующим образом:

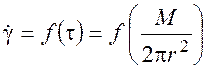. (4)

Из этой записи следует, что эффекты тиксотропии и реопексии лежат вне данной теории, хотя в принципе ротационные вискозиметры достаточно удобные приборы для изучения этих реологических нестационарностей. С математической точки зрения важно, чтобы функция (4) была однозначной и удовлетворяла обычным условиям непрерывности и дифференцируемости, что автоматически обеспечивает физическая природа реологического уравнения.

Из уравнений (3) и (4) запишем

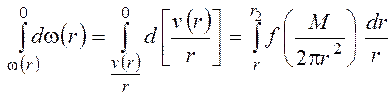. (5)

Заметим, что при записи верхних пределов интегрирования полагают прилипаемость жидкости к поверхности неподвижного цилиндра вискозиметра v (r ₂) = 0, w (r ₂) = 0. Проведя интегрирование и поменяв местами пределы интегрирования, получим

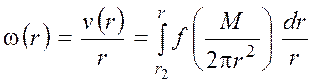. (6)

Продифференцируем первое уравнение из выражений (2.102) и немного его преобразуем:

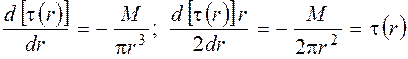. (7)

Тогда выражение (6) в новых переменных интегрирования в правой части, опять поменяв местами пределы интегрирования, можно переписать в виде

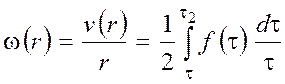. (8)

Чтобы связать напряжение с измеряемой на вискозиметре угловой скоростью ротора, примем текущий радиус за радиус ротора и запишем выражение (8) в виде

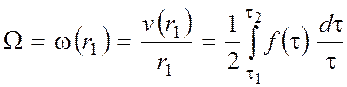. (9)

Выведем самое распространенное в теории ротационных вискозиметров – формулу Маргулеса. Примем за реологическое уравнение линейное уравнение ньютоновской жидкости и проведем интегрирование правой части выражения (9):

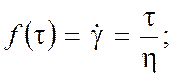
(10)

.

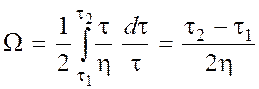Подставим в (10) величины касательных напряжений из формул (2.102) и получим формулу Маргулеса:

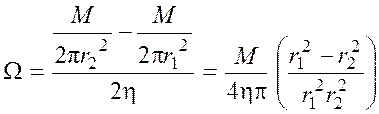. (11)

Следовательно, коэффициент динамической вязкости ньютоновской жидкости с аналитической точки зрения можно определить однократным измерением момента на роторе и угловой скорости его вращения:

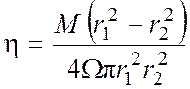. (12)

Повторные опыты нужно проводить лишь для получения статистических вероятностных показателей, на которые указывалось в начале данной главы. Поскольку момент и угловая скорость имеют разные знаки, коэффициент вязкости будет положительным. Формулу (12) можно использовать при вискозиметрировании таких текучих пищевых материалов, как, например, молоко, растительные масла и различные растворы и суспензии с малой концентрацией твердой фазы.

Если конструкция вискозиметра такова, что ротор вращается в условно-бесконечной среде жидкости, то нужно изменить краевые условия и проводить интегрирование по формуле (5) следующим образом:

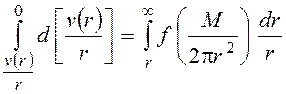. (13)

Далее аналогично (5)–(12) запишем

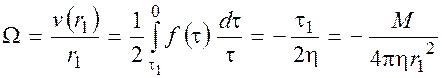(14)

или

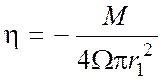. (15)

Этот же результат можно получить в пределе непосредственно из формулы (12):

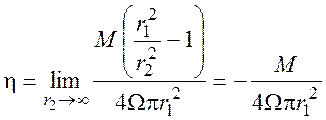. (16)

Иногда в формулах (12) и (16) приписывают сомножителем ускорение свободного падения, что не нужно делать, как легко установить из элементарного анализа размерностей в гостированной системе единиц СИ:

. (17)

В некоторых старых изданиях в качестве единицы измерения коэффициента внутреннего трения (вязкости) используется пуаз или сантипуаз, поэтому приведем связь между единицами:

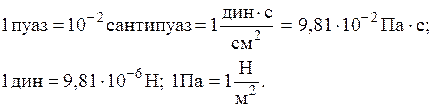(18)

Сомножитель, равный ускорению свободного падения, в формуле (12) появляется при переводе коэффициента вязкости из сантипуаз в единицы СИ [Па×с].

Во многих конструкциях вискозиметров типа вискозиметра Куэтта внешний цилиндр вращается с угловой скоростью W, а момент М измеряется на внутреннем неподвижном цилиндре с помощью тор-сионных измерительных систем, где момент является реактивным. В этом случае активный момент на внешнем цилиндре и угловая скорость совпадают по знаку. Приведем вывод формулы Маргулеса для данной конструкции, для чего выражение (5) перепишем в виде

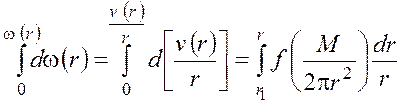. (19)

Далее, следуя выводу (5)–(12), запишем

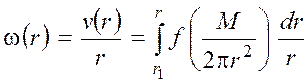; (20)

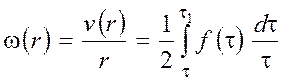; (21)

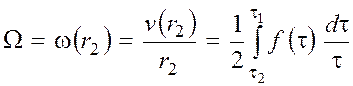. (22)

Подставим в (20) реологическое уравнение ньютоновской жидкости и определим распределение скоростей течения по радиусу:

;

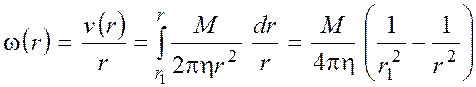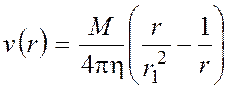. (23)

Из (22) получим угловую скорость:

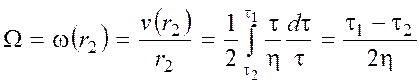. (24)

Откуда, аналогично (12), получим формулу Маргулеса для определения коэффициента динамической вязкости, с той только лишь разницей, что радиусы поменялись местами:

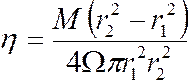
. (25)

В предыдущих решенных задачах на определенном этапе предполагали, что жидкость подчиняется реологическому уравнению Ньютона. В действительности при вискозиметрировании пищевых сред, особенно большой вязкости, это предположение не корректно. Мы не знаем вида реологического уравнения среды, а именно определение этого уравнения является целью ротационного вискозиметрирования, как и капиллярного вискозиметрирования, где эта проблема решалась с помощью уравнения Рабиновича.

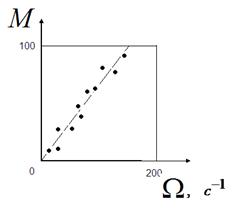
Рис. 2. Результаты измерений на ротационном вискозиметре

Расставить точки, составить таблицу и, задав радиусы вискозиметра, по методу средних по формуле Маргулеса рассчитать коэффициент динамической вязкости.

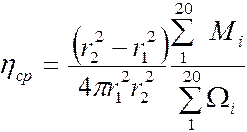
С помощью ПК провести расчет по методу наименьших квадратов и определить статистические параметры- стандартную ошибку и коэффициент корреляции..

Выводы:

Учитывая вышеизложенное, ротационная вискозиметрия требует проверки следующих требований, вытекающих из условий вывода предыдущих формул:

1. При вискозиметрии надо исключить концевые эффекты параллельными опытами на роторах разной длины и одного радиуса.

2. Необходимо обеспечить ламинарность течения.

3. Нужно проверить отсутствие пристенного проскальзывания.

4. Проверять среду на тиксотропию и реопексию.

5. Для жидкостей с ньютоновской вязкостью можно использовать формулу Маргулеса, для неньютоновских жидкостей при обработке данных вискозиметрирования надо использовать формулу Павловского.

Date: 2015-05-23; view: 1252; Нарушение авторских прав