
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема работы № 3. Определения индекса течения и коэффициента консистенции жидкости Оствальда – Де Виля и характеристик ее течения в трубе
|
|
Цель: Ознакомиться со свойствами и характеристиками течения степенных жидкостей
Задачи: Изучить:
реологическую формулу степенной жидкости;
реологическую кривую течения в координатах напряжение и скорость сдвига; уравнение Рабиновича;
объемный расход и эпюры скоростей течения ньютоновской и степенной жидкости в трубе;
линеаризация степенной зависимости
Ход работы:
Многие пищевые среды, являющиеся сложными дисперсными средами из многокомпонентных органических природных полимеров, не подчиняются закону вязкости Ньютона и их вязкостные свойства нельзя описать одним параметром – коэффициентом вязкости. Эти свойства исследуются с помощью вискозиметров и различных реометров. Такие жидкости называются неньютоновскими. Иногда в литературе встречается термин – аномальные. Примером таких жидкостей могут быть степенные жидкости, которые описываются законом Оствальда - Де Виля.
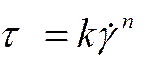
 (1)
(1)
где 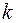 - реологическая константа, коэффициент консистенции;
- реологическая константа, коэффициент консистенции;
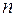 - реологическая константа, индекс течения,
- реологическая константа, индекс течения,
Этим законом описывается течение очень многих искусственных полимеров, а также смесей натуральных биологических органических полимеров – пищевых сред.
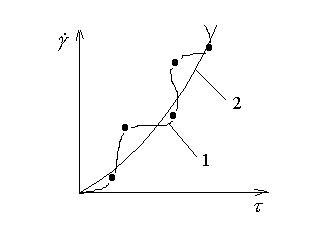
Рис. 1. Реологическая кривая течения в координатах напряжение и скорость сдвига. 1- кривая по точной интерполяционной формуле; 2 – действительная физически и экспериментально обоснованная кривая течения Оствальда-Де Виля степенной жидкости
Среди множества типов вискозиметров для исследования вязкостных свойств пищевых масс в первую очередь следует рекомендовать капиллярные и ротационные вискозиметры, потому что теория обработки данных измерений на этих приборах наиболее детально разработана. Причем если теория капиллярных вискозиметров проще, чем ротационных, и на капиллярных вискозиметрах сравнительно легко непосредственно моделировать и имитировать многие процессы формования и транспортирования пищевых масс, то при ротационной вискозиметрии требуется меньше испытываемой пищевой среды, проще достичь широкого диапазона скоростей сдвига и исследовать, кроме вязкостных свойств, вязкоупругие свойства пищевого продукта.
В литературе имеются также данные об инвариантности результатов капиллярной и ротационной вискозиметрии по сравнительному критерию инвариантности. Например, Кузнецов с сотрудниками исследовал свойства растворов желатина до 25 % на капиллярном вискозиметре типа Убеллоде–Гольда и на немецком ротационном вискозиметре «Реотест». Было обнаружено, что свойства высококонцентрированных растворов желатина можно описывать реологической моделью Шведова–Бингама, а сравнительная реометрия на двух указанных приборах дала совпадение результатов в пределах 5–15 %. Эти данные еще раз подтверждают совершенство теории капиллярных и ротационных вискозиметров и позволяют отнести эти вискозиметры к группе условно-абсолютных приборов, если следовать функциональной системе классификации реометров.
В опытах на капиллярных вискозиметрах обычно измеряются объемный или весовой расход протекающей среды и перепад давления при известных длине и диаметре капилляра. Задачей теории вискозиметра является определение связи между скоростями и напряжением сдвига в исследуемой среде безотносительно размеров капилляра. Рассматривая ламинарный изотермический стационарный осесимметричный поток среды в капилляре, легко по уравнению равновесия определить напряжение сдвига в любом коаксиальном слое капилляра:
(р 2 – р 1) p r 2 – 2p rL t = 0 (2)
и
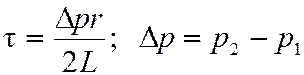 , (3)
, (3)
где t – напряжение сдвига на цилиндрической поверхности участка потока; r – радиус мысленно вырезанного цилиндрического осесимметричного участка потока, равновесие которого рассматривается; L – расстояние между поперечными сечениями капилляра; р 1, р 2 – давление в начальном и конечном поперечных сечениях капилляра.
Как видно, напряжение сдвига не зависит от вязкостных свойств среды. Теперь необходимо по измеренному объемному расходу определить скорость сдвига; она разная в каждом слое текущей жидкости и зависит от реологического закона сдвигового течения среды, а закон этот априорно неизвестен, поскольку определение его является целью вискозиметрии.
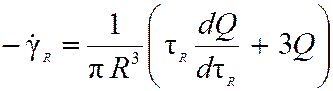 . (4)
. (4)
Формула (3) позволяет вычислить скорость сдвига на стенке капилляра. В этом же месте по формуле (2) можно рассчитать напряжение сдвига. Чтобы представить уравнение (3) через измеряемые при капиллярной вискозиметрии величины, воспользуемся еще раз формулой (2) и перепишем (3) в виде уравнения Рабиновича:
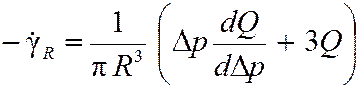 . (5)
. (5)
Таким образом, уравнения (4) и (2) лежат в основе теории капиллярной вискозиметрии и позволяют по измеренному объемному расходу и перепаду давления при известной геометрии капилляра без всяких предварительных предположений о виде связи между скоростью и напряжением сдвига получить эту искомую связь. Знак минус связан с тем, что D р < 0.
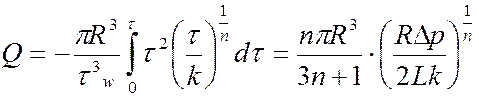 (6)
(6)
Это уравнение при определенных значениях индекса течения и коэффициента консистенции переходит в формулу Пуазейля.
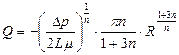
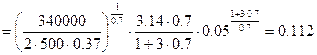 ,
, 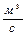 .
.
Построить эпюру скоростей степенной жидкости на эпюре скоростей течения ньютоновской жидкости по формулам (7) и (8):
степенная жидкость
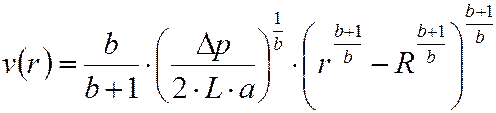 (7)
(7)
ньютоновская
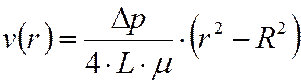 (8)
(8)
Далее:
1. В координатной системе у = у(х) (где х - скорость сдвига, в диапазоне 0 – 200, с-1; у - напряжение сдвига, в диапазоне 0 – 100, Па), провести две кривые, подобные изображенным на рис. 4 и рис. 5. В инженерной реологии, как уже указывалось в работе №1, приняты следующие обозначения: 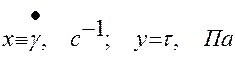 .
.
2.Вокруг кривых случайным образом расположить 20 (здесь в примерах 9) точек, моделируя этим результаты реометрии среды Оствальда-Де Виля (пример см. рис.4 и рис. 5)
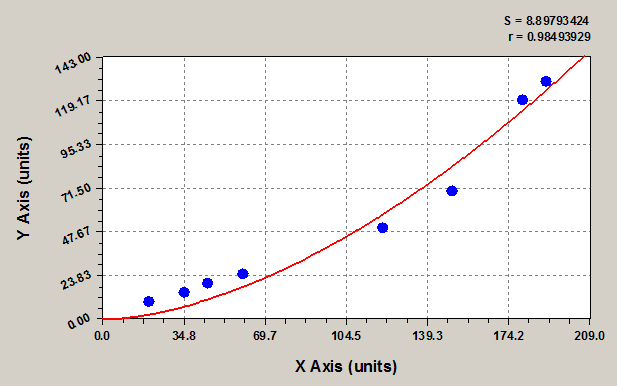
Рис.2. Результаты реометрии среды Оствальда –Де Виля в случае упрочнения структуры среды при росте скорости сдвига Кривая построена с помощью программы CurveExpert.
Таблица № 1
x y
20 10
35 15
45 20
60 25
120 50
150 70
180 120
190 130
User-Defined Model: y=a*x^b
Coefficient Data:
a = 0.017006493
b = 1.696882
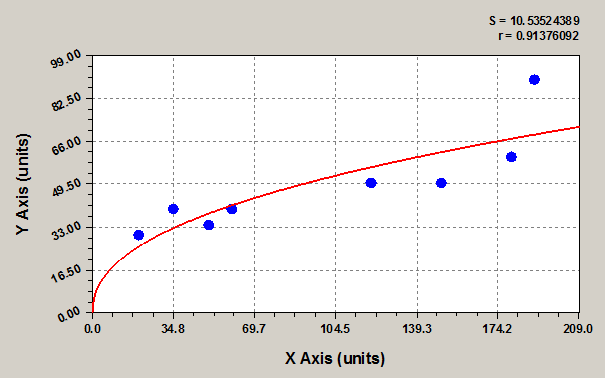
Рис.3. Результаты реометрии среды Оствальда –Де Виля в случае разрушения структуры среды при росте скорости сдвига. Кривая построена с помощью программы CurveExpert.
Таблица № 2.
20 30
35 40
50 34
60 40
120 50
150 50
180 60
190 90
User-Defined Model: y=a*x^b
Coefficient Data:
a = 6.8756474
b = 0.43899932
Составить таблицы № 1 и № 2 полученных таким образом экспериментальных данных.
Рассчитать коэффициенты консистенции и индексы течения для обоих случаев. В данных примерах:
User-Defined Model: y=a*x^b
Coefficient Data:
a = 0.017006493
b = 1.696882
User-Defined Model: y=a*x^b
Coefficient Data:
a = 6.8756474
b = 0.43899932
Рассчитать объемный расход при течении жидкости в трубе со следующими исходными данными с помощью Mathcad:
Дано: Индексы течения b и коэффициенты консистенции a.
1 случай:
a = 0.017006493
b = 1.696882
2 случай:
a = 6.8756474
b = 0.43899932
R=0.05 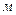 -радиус трубы;
-радиус трубы;
L=500 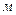 -длина трубы;
-длина трубы;
p=340000 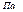 -перепад давлений
-перепад давлений
Решение:
1 случай:
a = 0.017006493
b = 1.696882
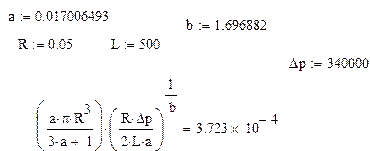
2 случай:
a = 6.8756474
b = 0.43899932
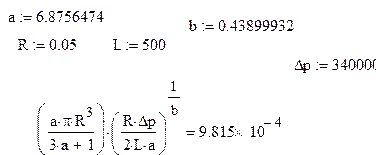
Построить эпюры скоростей течения жидкости в трубе степенной и ньютоновской жидкостей:
| С р а в н е н и е э п ю р с к о р о с т е й с т е п е н н о й и н ь ю т о н о в с к о й ж и д к о с т е й |
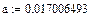
|
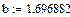
|
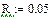
|

|

|
| С т е п е н н а я ж и д к о с т ь |
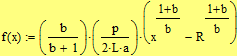
|
| н ь ю т о н о в с к а я ж и д к о с т ь |
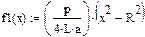
|
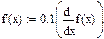
|
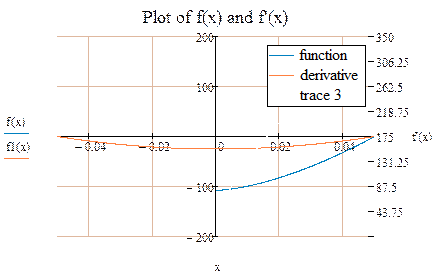
| П р о и з в о д н а я -бе с ц в е т н а я |
| С т е п е н н а я ж и д к о с т ь -с и н я я н ь ю т о н о в с к а я ж и д к о с т ь - к р а с н а я |
|
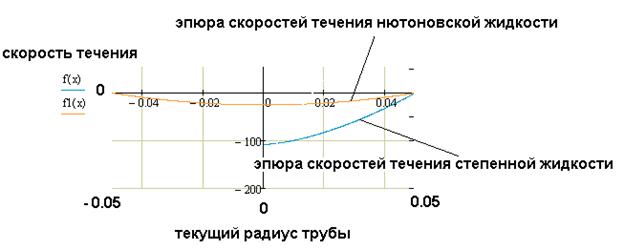
Рис.4. Эпюры скоростей течения степенной и ньютоновской жидкостей в трубе
Рассчитать по методу средних и с помощью математической программы на ПК реологические константы степенной жидкости, пересчитав данные таблицы № 1 и 2 в логарифмах (линеаризация степенной зависимости)
Воспользуемся данными из таблиц, найдём коэффициенты n и k, используя логарифмирование.
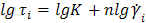
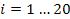
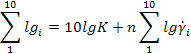
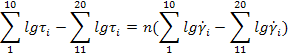
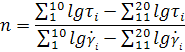
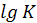 =
= 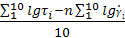
Выводы
- Степенное реологическое уравнение можно линеализировать логарифмированием
и использовать метод средних для определения индекса течения и коэффициента консистенции.
2.. Если индекс течения меньше единицы, то кривая течения искривляется в верх, если больше единицы – то направо (см. рисунки), если индекс течения равен единице – то это не степенная жидкость, а ньютоновская и коэффициент консистенции является коэффициентом динамической вязкости.
Тема работы № 4. Определения по результатам капиллярной вискозиметрии предельного напряжения сдвига и коэффициента пластической вязкости среды Шведова-Бингама и характеристики ее течения в трубе
Цель: Ознакомиться со средой Шведова-Бингама
Задачи: Рассмотреть течение неньютоновских жидкостей в трубах, определить зависимости между пропускной способностью и перепадом давления при ламинарном течении в круглых трубах, научиться вычислять профиль скоростей течения среды Шведова-Бингама.
Ход работы:
Для напряжения трения на стенке получаем:
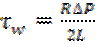 (1)
(1)
Интегрирование дает:
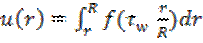 ,(2)
,(2)
Поскольку u(R)=0 при допущении справедливости условия прилипания жидкости на стенке (отсутствие скольжения). Далее находим:
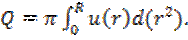 (3)
(3)
Интегрирование по частям даёт:
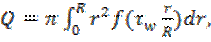 (4)
(4)
Так как и (R)=0.
Бингамовский пластик.
Исходным соотношением является: 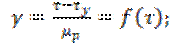
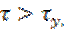
Где f(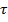 ) – непрерывная функция такая, что
) – непрерывная функция такая, что
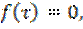 0<
0< 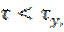
И
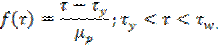
При течении в трубе напряжения трения падают до нуля на оси, а в приосевой области, где напряжения сдвига ниже предела текучести 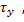 материал не подвергается сдвигу, перемещаясь вдоль как твёрдый стержень. Это иллюстрирует профиль скоростей.
материал не подвергается сдвигу, перемещаясь вдоль как твёрдый стержень. Это иллюстрирует профиль скоростей.
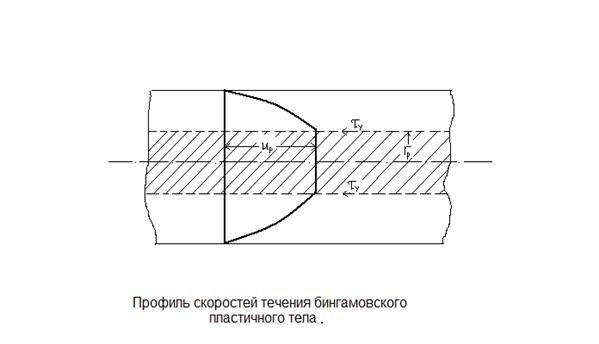
Подстановка 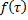 в формулу (4) даёт:
в формулу (4) даёт:
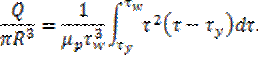
Выполняя интегрирование и подставив 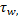 получим формулу:
получим формулу:
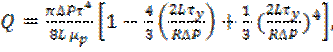 (5)
(5)
Известную под названием формула Букингема-Рейнера. Это уравнение нельзя разрешить относительно перепада давления. Когда предел текучести равен нулю, оно совпадает с формулой Пуазейля. Колдуэлл и Бэбит успешно применили уравнение Букингема к задаче о течении грязей и шламов.
Для бингамовского идеально пластичного тела имеем:
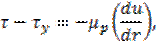
Интегрирование последнего выражения даёт:
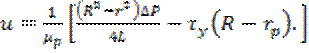 (6)
(6)
С учётом, что u=0 при r=R.
Вблизи оси материал будет двигаться как твёрдый цилиндрический стержень с радиусом
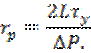
Подставив отсюда значение радиуса в (6), получим скорость квазитвёрдого движения:
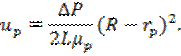
Для известных значений 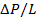 ,
, 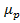 и
и 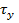 профиль скоростей можно вычислить из формул (5) и (6).Соответствующий расход определяется уравнением (5).
профиль скоростей можно вычислить из формул (5) и (6).Соответствующий расход определяется уравнением (5).
Задание: рассчитать предельное напряжение сдвига и коэффициент пластической вязкости, построить эпюру скоростей течения.
Начертить координатную плоскость Произвольно провести прямую С из начала координат. Вокруг прямой С произвольно расставить 20 точек и на основании координат этих точек составить таблицу.
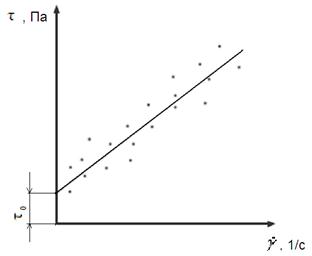
Рис.1. Имитация результатов реометрии среды Шведова –Бингама.
Реологическое уравнение Шведова-Бингама имеет вид: 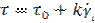
Находим коэффициент К, используя систему уравнения:
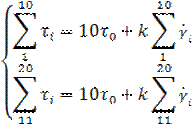
Отсюда вычисляем коэффициент К:
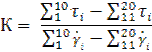
 Находим τ0 по формуле:
Находим τ0 по формуле:
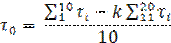
Рассчитаем радиус x0 жесткого ядра потока и скорость потока V.
Из уравнения равновесия получим:
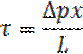
Предельное напряжение сдвига 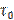 определяет толщину
определяет толщину 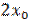 жесткого ядра потока:
жесткого ядра потока:
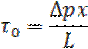
Реологическое уравнение Шведова-Бингама имеет вид:

 к виду, удобному для интегрирования:
к виду, удобному для интегрирования:
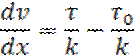
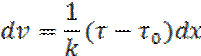
Произведём замену переменных 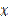 →
→ 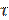 и интегрируем:
и интегрируем:
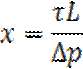
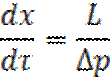
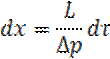
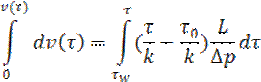
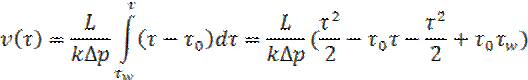
Определим скорость потока ядра:
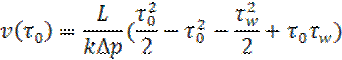
Касательное напряжение на стенке канала определяет формула вида:
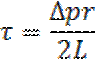
Вычисляем радиус стержневого потока(ядра):
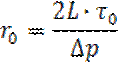
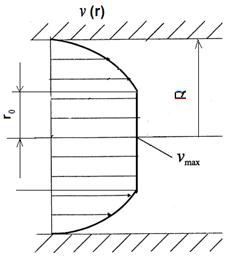
Рис.10. Эпюра скоростей течения среды Шведова-Бингама
Выводы:
- Среда Шведова –Бингама деформируется упруго и не течет, когда напряжение на стенке капилляра меньше предельного напряжения сдвига.
- При течении среды Шведова-Бингама в трубе образуется центральное ядро, в котором скорости течения одинаковые и не зависят от текущего радиуса (см. рис.10).
- Расход при течении среды Шведова –Бингама в трубе определяется формулой Букингема-Рейнера (см. формулу (5))
Date: 2015-05-23; view: 3022; Нарушение авторских прав