
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розрахункові завдання. Задача 1.Обчислити визначник
|
|
Задача 1. Обчислити визначник.
1.1. 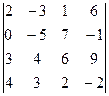 . 1.2.
. 1.2. 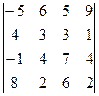 .
.
1.3. 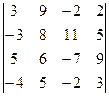 . 1.4.
. 1.4. 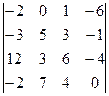 .
.
1.5. 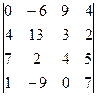 . 1.6.
. 1.6. 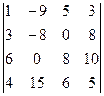 .
.
1.7. 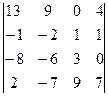 . 1.8.
. 1.8. 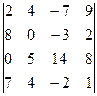 .
.
1.9. 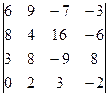 . 1.10.
. 1.10. 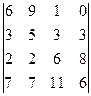 .
.
1.11. 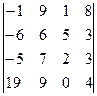 . 1.12.
. 1.12. 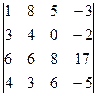 .
.
1.13. 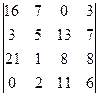 . 1.14.
. 1.14. 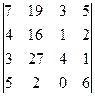 .
.
1.15. 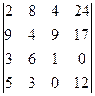 . 1.16.
. 1.16. 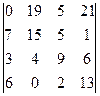 .
.
1.17. 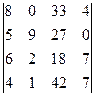 . 1.18.
. 1.18. 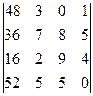 ;.
;.
1.19. 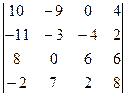 . 1.20.
. 1.20. 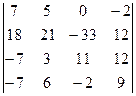 .
.
1.21. 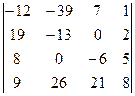 . 1.22.
. 1.22. 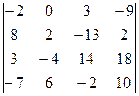 .
.
1.23. 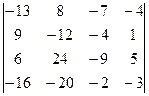 . 1.24.
. 1.24. 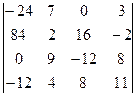 .
.
1.25. 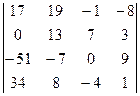 . 1.26.
. 1.26. 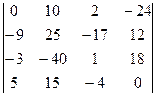 .
.
1.27. 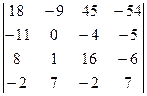 . 1.28.
. 1.28. 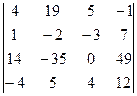 .
.
1.29. 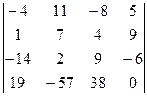 . 1.30.
. 1.30. 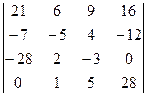 .
.
Задача 2. Знайти всі значення 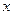 , при яких задана матриця є виродженою.
, при яких задана матриця є виродженою.
2.1. 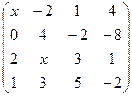 . 2.2.
. 2.2. 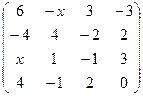 .
.
2.3. 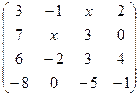 . 2.4.
. 2.4. 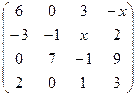 .
.
2.5. 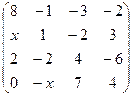 . 2.6.
. 2.6. 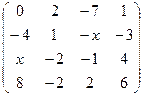 .
.
2.7. 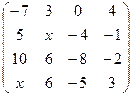 . 2.8.
. 2.8. 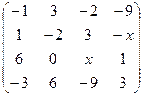 .
.
2.9. 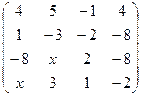 . 2.10.
. 2.10. 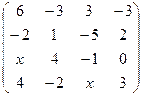 .
.
2.11. 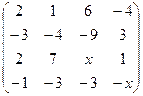 . 2.12.
. 2.12. 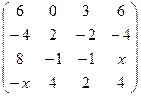 .
.
2.13. 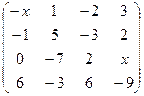 . 2.14.
. 2.14. 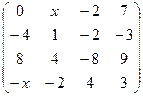 .
.
2.15. 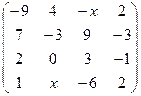 . 2.16.
. 2.16. 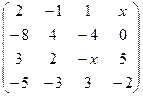 .
.
2.17. 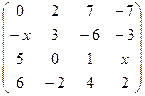 . 2.18.
. 2.18. 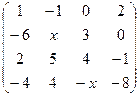 .
.
2.19. 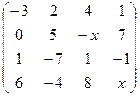 . 2.20.
. 2.20. 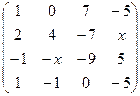 .
.
2.21. 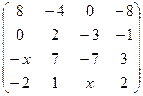 . 2.22.
. 2.22. 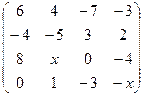 .
.
2.23. 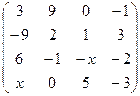 . 2.24.
. 2.24. 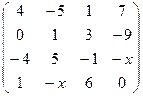 .
.
2.25.  . 2.26.
. 2.26. 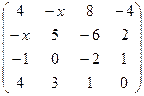 .
.
2.27. 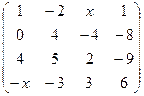 . 2.28.
. 2.28. 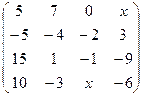 .
.
2.29. 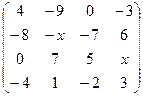 . 2.30.
. 2.30. 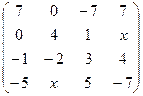 .
.
Задача 3. Знайти 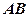 та
та 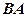 , якщо:
, якщо:
3.1. 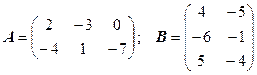 .
.
3.2. 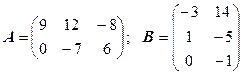 .
.
3.3. 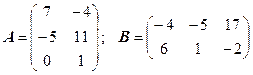 .
.
3.4. 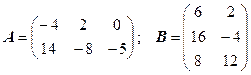 .
.
3.5. 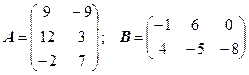 .
.
3.6. 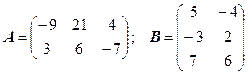 .
.
3.7. 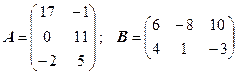 .
.
3.8. 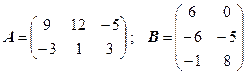 .
.
3.9. 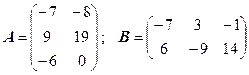 .
.
3.10. 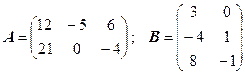 ;
;
3.11. 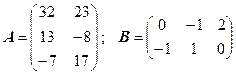 .
.
3.12. 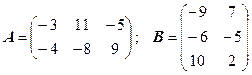 .
.
3.13. 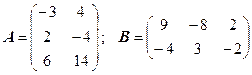 ;
;
3.14. 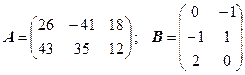 .
.
3.15. 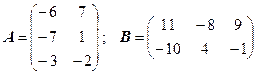 .
.
3.16. 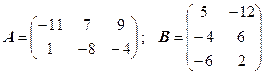 .
.
3.17. 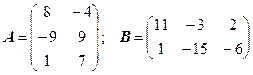 .
.
3.18. 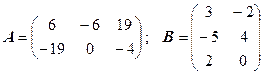 .
.
3.19. 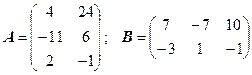 .
.
3.20. 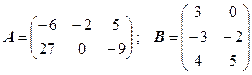 .
.
3.21. 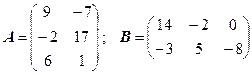 .
.
3.22. 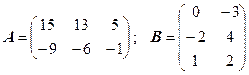 .
.
3.23. 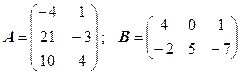 .
.
3.24. 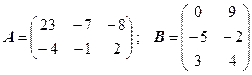 .
.
3.25. 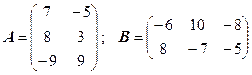 .
.
3.26. 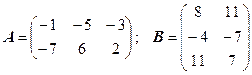 .
.
3.27. 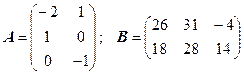 .
.
3.28. 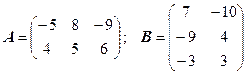 .
.
3.29. 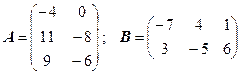 .
.
3.30. 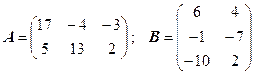 .
.
Задача 4. Перевірити, чи для заданої матриці існує обернена. У випадку існування знайти її.
4.1. 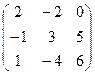 . 4.2.
. 4.2. 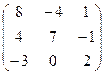 .
.
4.3. 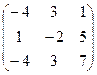 . 4.4.
. 4.4. 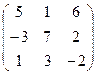 .
.
4.5. 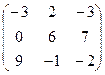 . 4.6.
. 4.6. 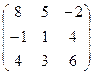 .
.
4.7. 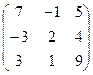 . 4.8.
. 4.8. 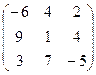 .
.
4.9. 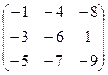 . 4.10.
. 4.10. 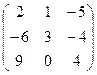 .
.
4.11. 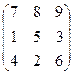 . 4.12.
. 4.12. 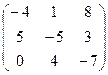 .
.
4.13. 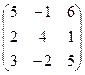 . 4.14.
. 4.14. 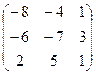 .
.
4.15. 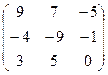 . 4.16.
. 4.16. 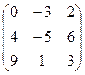 .
.
4.17. 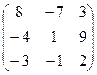 . 4.18.
. 4.18. 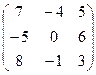 .
.
4.19. 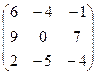 . 4.20.
. 4.20. 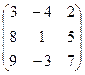 .
.
4.21. 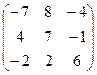 . 4.22.
. 4.22. 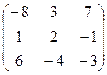 .
.
4.23. 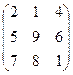 . 4.24.
. 4.24. 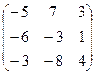 .
.
4.25. 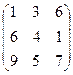 . 4.26.
. 4.26. 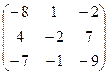 .
.
4.27.  . 4.28.
. 4.28. 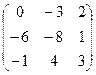 .
.
4.29..4.30..
Задача 5. Чи утворює лінійний простір задана множи-на, в якій визначені сума будь-яких двох елементів 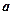 та
та 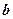 і добуток довільного елемента
і добуток довільного елемента 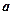 на довільне дійсне число
на довільне дійсне число 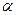 ?
?
5.1. Множина всіх вироджених матриць 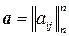 ,
, 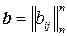 , сума
, сума 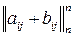 , добуток
, добуток 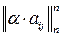 .
.
5.2. Множина всіх невироджених матриць 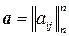 ,
, 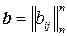 , сума
, сума 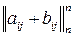 , добуток
, добуток 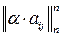 .
.
5.3. Множина всіх матриць 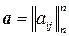 ,
, 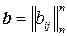 , сума
, сума 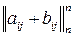 , добуток
, добуток 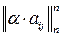 .
.
5.4. Множина всіх матриць 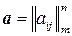 ,
, 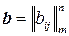 , сума
, сума 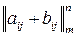 , добуток
, добуток 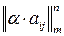 .
.
5.5. Множина всіх вироджених матриць 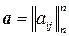 ,
, 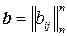 , сума
, сума 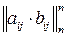 , добуток
, добуток 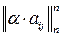 .
.
5.6. Множина всіх невироджених матриць 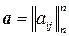 ,
, 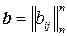 , сума
, сума 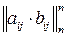 , добуток
, добуток 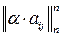 .
.
5.7. Множина всіх матриць 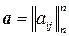 ,
, 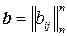 , сума
, сума 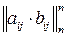 , добуток
, добуток 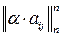 .
.
5.8. Множина всіх матриць 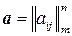 ,
, 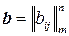 , сума
, сума 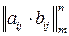 , добуток
, добуток 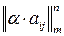 .
.
5.9. Множина всіх вироджених матриць 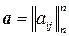 ,
, 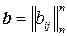 , сума
, сума 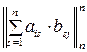 , добуток
, добуток 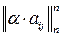 .
.
5.10. Множина всіх невироджених матриць 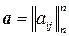 ,
, 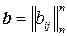 , сума
, сума 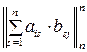 , добуток
, добуток 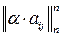 .
.
5.11. Множина всіх матриць 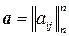 ,
, 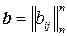 , сума
, сума 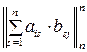 , добуток
, добуток 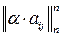 .
.
5.12. Множина всіх многочленів п¢ятого степеня від змін-ної х: 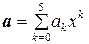 ,
, 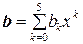 ,
, 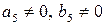 ; сума
; сума 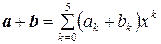 , добуток
, добуток 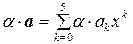 .
.
5.13. Множина всіх многочленів не вище п¢ятого степеня від змінної х: 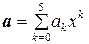 ,
, 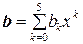 ; сума
; сума 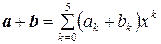 , добуток
, добуток 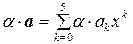 .
.
5.14. Множина всіх періодичних функцій 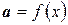 ,
, 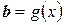 з однаковим періодом, визначених на
з однаковим періодом, визначених на 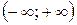 ; сума
; сума 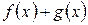 , добуток
, добуток 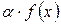 .
.
5.15. Множина всіх періодичних функцій 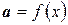 ,
, 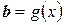 (не обов¢язково з однаковим періодом), визначених на
(не обов¢язково з однаковим періодом), визначених на 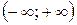 ; сума
; сума 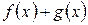 , добуток
, добуток 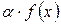 .
.
5.16. Множина всіх неперіодичних функцій 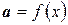 ,
, 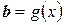 , визначених на
, визначених на 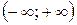 ; сума
; сума 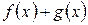 , добуток
, добуток 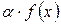 .
.
5.17. Множина всіх парних функцій 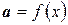 ,
, 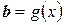 , визначених на
, визначених на 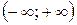 ; сума
; сума 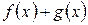 , добуток
, добуток 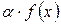 .
.
5.18. Множина всіх непарних функцій 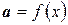 ,
, 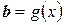 , визначених на
, визначених на 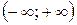 ; сума
; сума 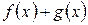 , добуток
, добуток 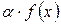 .
.
5.19. Множина всіх функцій 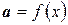 ,
, 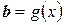 , визначе-них на
, визначе-них на 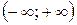 , які не є ні парними, ні непарними; сума
, які не є ні парними, ні непарними; сума 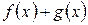 , добуток
, добуток 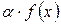 .
.
5.20. Множина всіх збіжних послідовностей 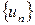 ,
, 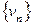 ; сума
; сума 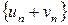 , добуток
, добуток 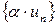 .
.
5.21. Множина всіх розбіжних послідовностей 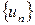 ,
, 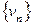 ; сума
; сума 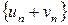 , добуток
, добуток 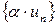 .
.
5.22. Множина всіх векторів тривимірного простору, які лежать на одній осі; сума 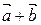 , добуток
, добуток 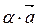 .
.
5.23. Множина всіх векторів тривимірного простору, які не лежать на одній осі; сума 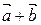 , добуток
, добуток 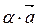 .
.
5.24. Множина всіх векторів тривимірного простору, в кожного з яких друга координата дорівнює нулю; сума 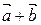 , добуток
, добуток 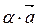 .
.
5.25. Множина всіх векторів тривимірного простору, в кожного з яких хоча б одна з координат дорівнює нулю; сума 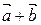 , добуток
, добуток 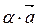 .
.
5.26. Множина всіх векторів тривимірного простору, в кожного з яких рівно одна координата дорівнює нулю; сума 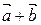 , добуток
, добуток 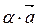 .
.
5.27. Множина всіх векторів тривимірного простору; сума - векторний 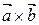 , добуток
, добуток 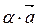 .
.
5.28. Множина всіх цілих чисел; сума 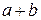 , добуток
, добуток 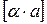 , де
, де 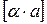 - ціла частина числа
- ціла частина числа 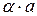 .
.
5.29. Множина всіх дійсних чисел; сума 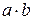 , добуток -
, добуток - 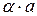 .
.
5.30. Множина всіх від¢ємних дійсних чисел; сума 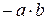 , добуток -
, добуток - 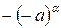 .
.
Задача 6. Перевірити, чи система елементів є лінійно залежною.
6.1. 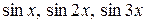 на інтервалі
на інтервалі 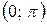 .
.
6.2. 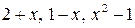 на відрізку
на відрізку 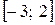 .
.
6.3. 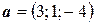 ,
, 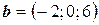 ,
, 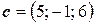 .
.
6.4. 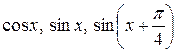 на інтервалі
на інтервалі 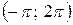 .
.
6.5. 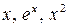 на відрізку
на відрізку 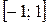 .
.
6.6.  ,
, 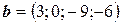 ,
, 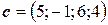 .
.
6.7. 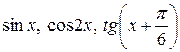 на проміжку
на проміжку  .
.
6.8. 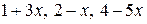 на інтервалі
на інтервалі 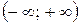 .
.
6.9. 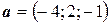 ,
, 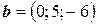 ,
, 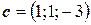 .
.
6.10. 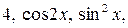 на інтервалі
на інтервалі 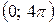 .
.
6.11. 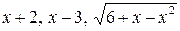 на відрізку
на відрізку 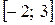 .
.
6.12.  ,
, 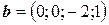 ,
, 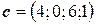 .
.
6.13. 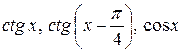 на проміжку
на проміжку 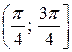 .
.
6.14. 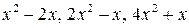 на інтервалі
на інтервалі 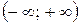 .
.
6.15. 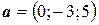 ,
, 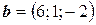 ,
, 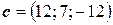 .
.
6.16. 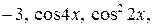 на інтервалі
на інтервалі  .
.
6.17. 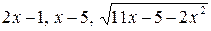 на відрізку
на відрізку 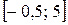 .
.
6.18. 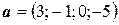 ,
, 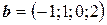 ,
, 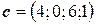 .
.
6.19. 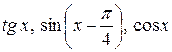 на проміжку
на проміжку 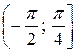 .
.
6.20. 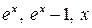 на інтервалі
на інтервалі 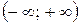 .
.
6.21. 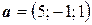 ,
, 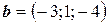 ,
, 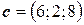 .
.
6.22. 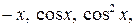 на інтервалі
на інтервалі 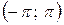 .
.
6.23. 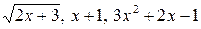 на відрізку
на відрізку 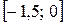 .
.
6.24. 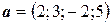 ,
, 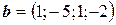 ,
, 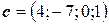 .
.
6.25. 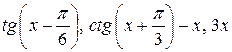 на проміжку
на проміжку
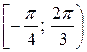 .
.
6.26. 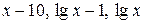 на інтервалі
на інтервалі 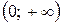 .
.
6.27. 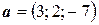 ,
, 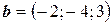 ,
,  .
.
6.28. 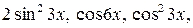 на інтервалі
на інтервалі 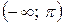 .
.
6.29. 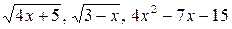 на відрізку
на відрізку
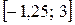 .
.
6.30. 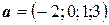 ,
, 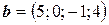 ,
, 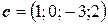 .
.
Задача 7. Знайти ранг матриці.
7.1. 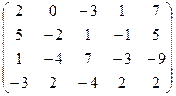 .
.
7.2. 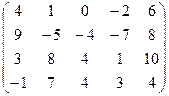 . 7.3.
. 7.3. 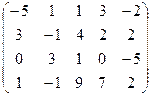 .
.
7.4.  .
.
7.5. 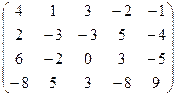 .
.
7.6. 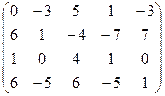 . 7.7.
. 7.7. 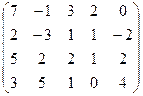 .
.
7.8. 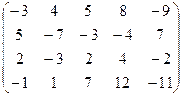 .
.
7.9. 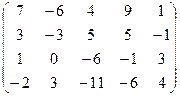 .
.
7.10. 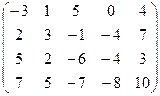 .
.
7.11. 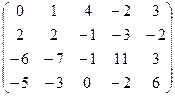 .
.
7.12. 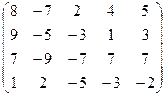 .
.
7.13. 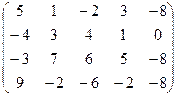 .
.
7.14. 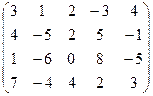 .
.
7.15. 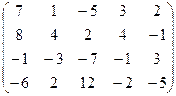 .
.
7.16. 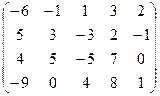 . 7.17.
. 7.17. 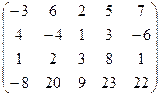 .
.
7.18. 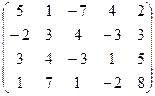 . 7.19.
. 7.19. 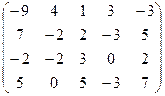 .
.
7.20. 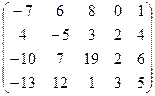 . 7.21.
. 7.21. 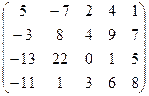 .
.
7.22. 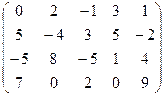 . 7.23.
. 7.23. 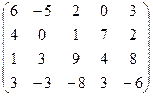 .
.
7.24. 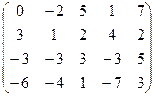 . 7.25.
. 7.25. 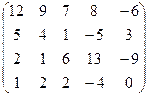 .
.
7.26. 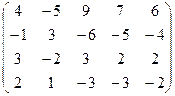 .
.
7.27. 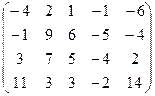 . 7.28.
. 7.28. 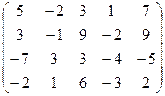 .
.
7.29. 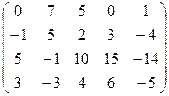 . 7.30.
. 7.30. 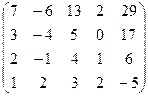 .
.
Задача 8. Довести сумісність даної системи лінійних алгебраїчних рівнянь і розв’язати її: а) методом Гаусса; б) ма-тричним методом; в) методом Крамера.
8.1. 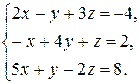 8.2.
8.2. 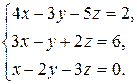
8.3. 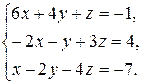 8.4.
8.4. 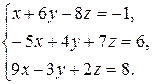
8.5. 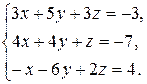 8.6.
8.6. 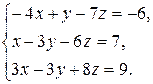
8.7. 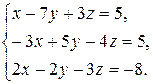 8.8.
8.8. 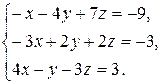
8.9. 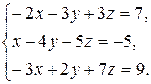 8.10.
8.10. 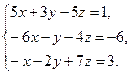
8.11. 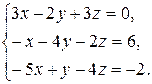 8.12.
8.12. 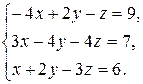
8.13. 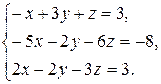 8.14.
8.14. 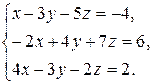
8.15. 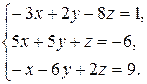 8.16.
8.16. 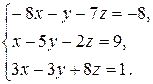
8.17. 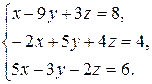 8.18
8.18 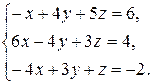
8.19. 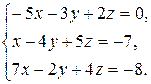 8.20.
8.20. 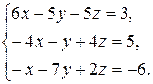
8.21. 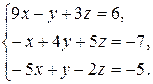 8.22.
8.22. 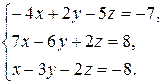
8.23. 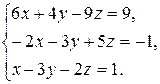 8.24.
8.24. 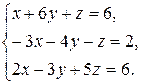
8.25. 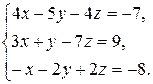 8.26.
8.26. 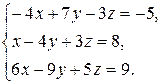
8.27. 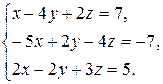 8.28.
8.28. 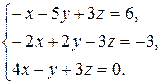
8.29. 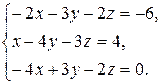 8.30.
8.30. 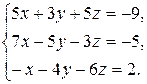
Задача 9. Розв¢язати однорідну систему лінійних алге-браїчних рівнянь, визначивши при цьому розмірність лінійно-го простору – множини розв¢язків даної системи і вказавши який-небудь базис цього простору.
9.1. 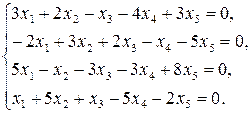
9.2. 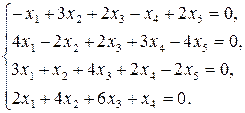
9.3. 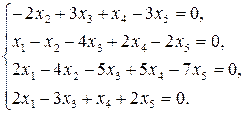
9.4. 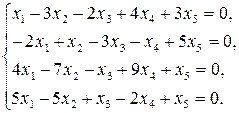
9.5. 
9.6. 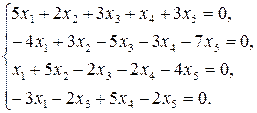
9.7. 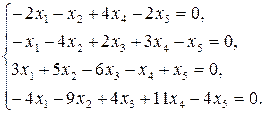
9.8. 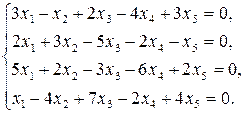
9.9. 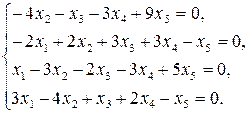
9.10. 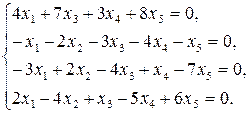
9.11. 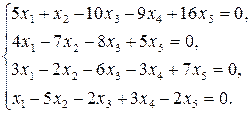
9.12. 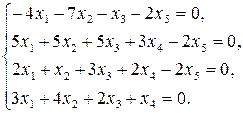
9.13. 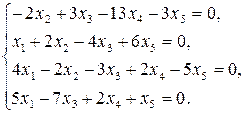
9.14. 
9.15. 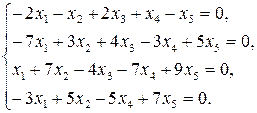
9.16. 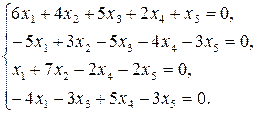
9.17. 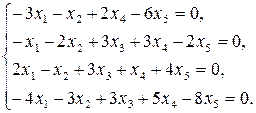
9.18. 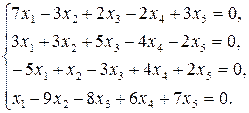
9.19. 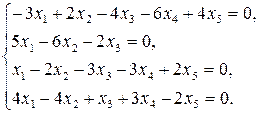
9.20. 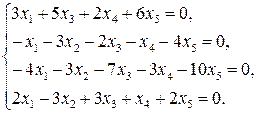
9.21. 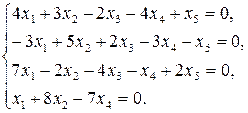
9.22. 
9.23. 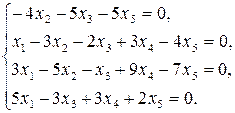
9.24. 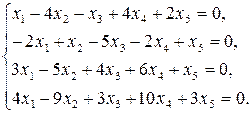
9.25. 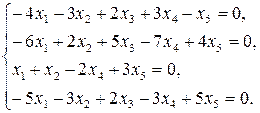
9.26. 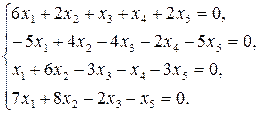
9.27. 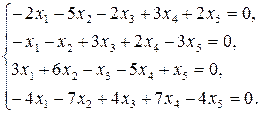
9.28. 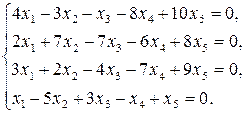
9.29. 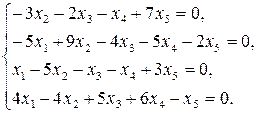
9.30. 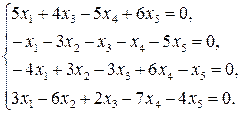
Задача 10. Визначити при яких 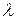 однорідна система лінійних алгебраїчних рівнянь має нетривіальні розв¢язки і знайти ці розв¢язки.
однорідна система лінійних алгебраїчних рівнянь має нетривіальні розв¢язки і знайти ці розв¢язки.
10.1. 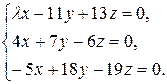 10.2.
10.2. 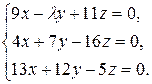
10.3. 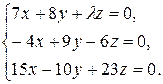 10.4.
10.4. 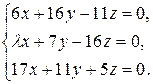
10.5. 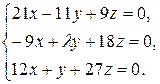 10.6.
10.6. 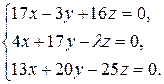
10.7. 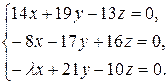 10.8.
10.8. 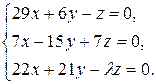
10.9. 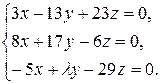
10.10. 
10.11. 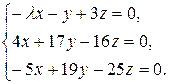
10.12. 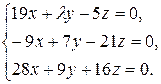
10.13. 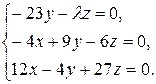
10.14. 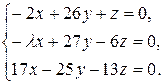
10.15. 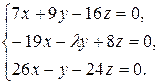
10.16. 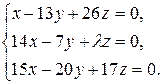
10.17. 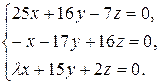
10.18. 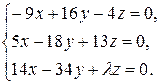
10.19. 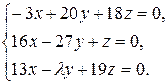
10.20. 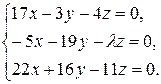
10.21. 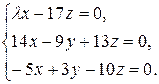
10.22. 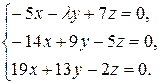 10.23.
10.23. 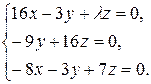
10.24. 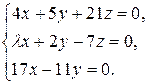 10.25.
10.25. 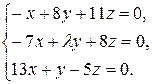
10.26. 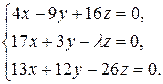
10.27. 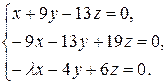
10.28. 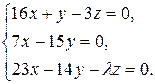
10.29. 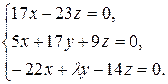
10.30. 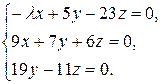
Задача 11. Лінійний оператор 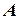 заданий в деякому базисі
заданий в деякому базисі 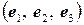 матрицею
матрицею 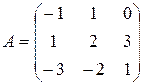 . Знайти матрицю
. Знайти матрицю 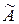 цього лінійного оператора в базисі
цього лінійного оператора в базисі 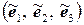 , якщо:
, якщо:
11.1. 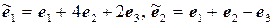 ,
,
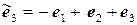 .
.
11.2. 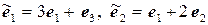 ,
, 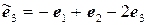 .
.
11.3. 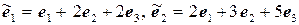 ,
,
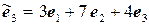 .
.
11.4. 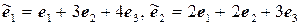 ,
,
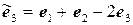 .
.
11.5. 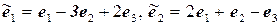 ,
,
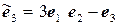 .
.
11.6. 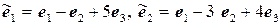 ,
,
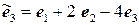 .
.
11.7. 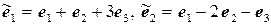 ,
,
 .
.
11.8. 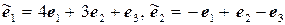 ,
,
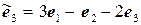 .
.
11.9. 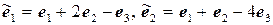 ,
, 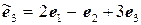 .
.
11.10. 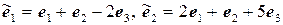 ,
, 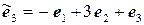 .
.
11.11. 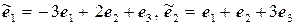 ,
, 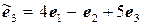 .
.
11.12. 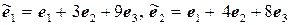 ,
, 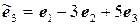 .
.
11.13. 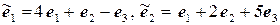 ,
, 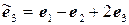 .
.
11.14.  ,
, 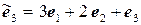 .
.
11.15. 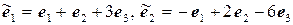 ,
, 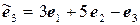 .
.
11.16. 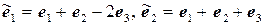 ,
, 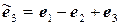 .
.
11.17. 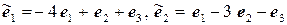 ,
, 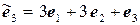 .
.
11.18. 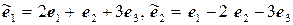 ,
, 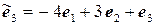 .
.
11.19. 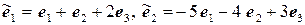 ,
, 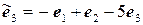 .
.
11.20. 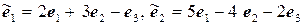 ,
, 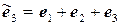 .
.
11.21. 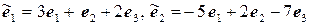 ,
, 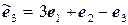 .
.
11.22. 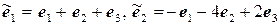 ,
, 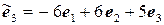 .
.
11.23. 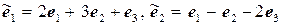 ,
, 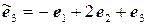 .
.
11.24. 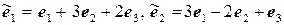 ,
, 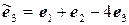 .
.
11.25. 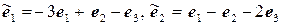 ,
, 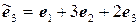 .
.
11.26. 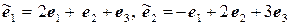 ,
, 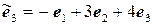 .
.
11.27. 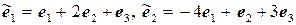 ,
, 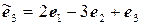 .
.
11.28. 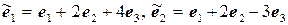 ,
, 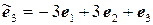 .
.
11.29. 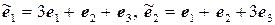 ,
, 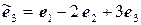 .
.
11.30. 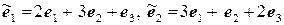 ,
, 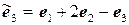 .
.
Задача 12. Знайти власні значення та власні вектори лінійного оператора, заданого в деякому базисі матрицею.
12.1.. 12.2..
12.3.. 12.4..
12.5.. 12.6..
12.7.. 12.8..
12.9.. 12.10..
12.11.. 12.12..
12.13.. 12.14..
12.15.. 12.16..
12.17.. 12.18..
12.19.. 12.20..
12.21.. 12.22..
12.23.. 12.24..
12.25.. 12.26..
12.27.. 12.28..
12.29.. 12.30..
Задача 13. Самоспряжений лінійний оператор 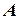 заданий матрицею А в деякому ортонормованому базисі
заданий матрицею А в деякому ортонормованому базисі 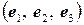 . Знайти: 1)
. Знайти: 1) 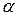 та
та 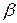 ; 2) власний ортонормований базис. Записати відповідну матриці А квадратичну форму в заданому базисі та її канонічний вигляд у власному базисі.
; 2) власний ортонормований базис. Записати відповідну матриці А квадратичну форму в заданому базисі та її канонічний вигляд у власному базисі.
13.1.  . 13.2.
. 13.2. 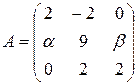 .
.
13.3. 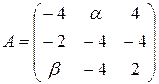 . 13.4.
. 13.4. 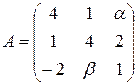 .
.
13.5. 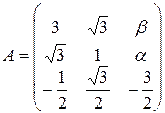 . 13.6.
. 13.6. 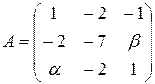 .
.
13.7. 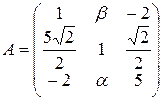 .
.
13.8. 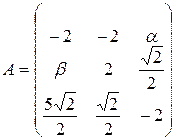
.
13.9. 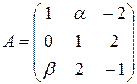 .
.
13.10. 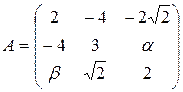 .
.
13.11. 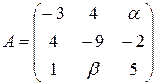 .
.
13.12. 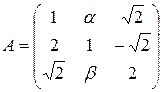 .
.
13.13. 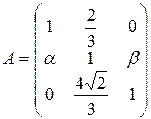 . 13.14.
. 13.14. 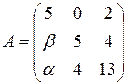 .
.
13.15. 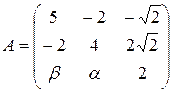 . 13.16.
. 13.16. 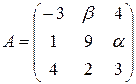 .
.
13.17. 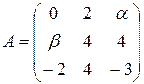 . 13.18.
. 13.18. 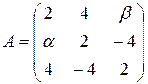 .
.
13.19. 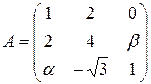 . 13.20.
. 13.20. 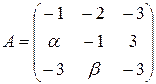 .
.
13.21. 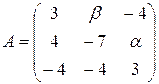 . 13.22.
. 13.22. 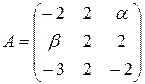 .
.
13.23. 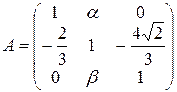 .
.
13.24.  . 13.25.
. 13.25. 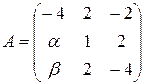 .
.
13.26. 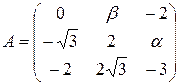 .
.
13.27. 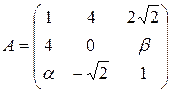 .
.
13.28. 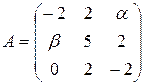 . 13.29.
. 13.29. 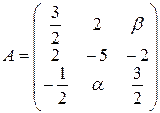 .
.
13.30. 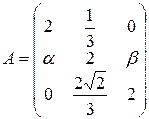 .
.
Задача 14. Звести до канонічного вигляду алгебраїчне рівняння другого порядку, вказавши його тип, і побудувати лінію, задану цим рівнянням.
14.1. 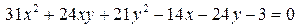 .
.
14.2. 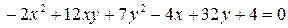 .
.
14.3. 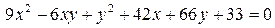 .
.
14.4. 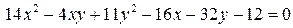 .
.
14.5. 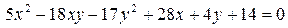 .
.
14.6. 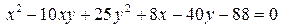 .
.
14.7. 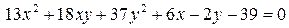 .
.
14.8. 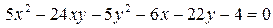 .
.
14.9. 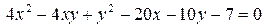 .
.
14.10. 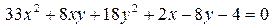 .
.
14.11. 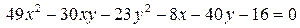 .
.
14.12. 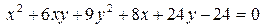 .
.
14.13. 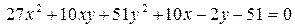 .
.
14.14. 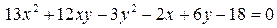 .
.
14.15. 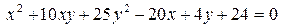 .
.
14.16. 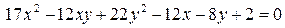 .
.
14.17. 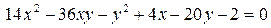 .
.
14.18. 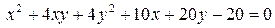 .
.
14.19. 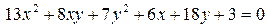 .
.
14.20. 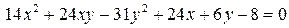 .
.
14.21. 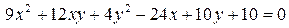 .
.
14.22. 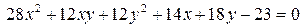 .
.
14.23. 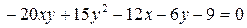 .
.
14.24. 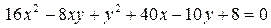 .
.
14.25. 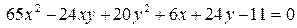 .
.
14.26. 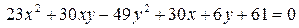 .
.
14.27. 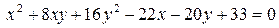 .
.
14.28. 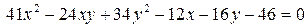 .
.
14.29. 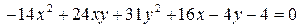 .
.
14.30. 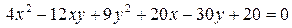 .
.
Date: 2015-04-23; view: 641; Нарушение авторских прав