Розрахункові завдання

Векторна алгебра та аналітична геометрія

Теоретичні питання

1. Поняття вектора. Лінійні операції над векторами, їх властивості.

2. Проекція вектора на вісь, її властивості.

3. Розклад вектора за базисом.

4. Декартові система координат на площині і в просторі.

5. Скалярний добуток векторів.

6. Векторний добуток векторів.

7. Мішаний добуток векторів.

8. Полярні координати на площині. Перетворення прямокутних координат.

9. Поняття про рівняння лінії на площині.

10. Різні форми рівняння прямої на площині. Кут між прямими. Відстань від точки до прямої.

11. Криві другого порядку: коло, еліпс, гіпербола, парабола.

12. Поняття про рівняння поверхні і лінії в просторі.

13. Різні форми рівнянь площини в просторі. Кут між площинами. Відстань від точки до площини.

14. Різні форми рівнянь прямої в просторі. Кут між прямими відстань від точки до прямої.

15. Пряма і площина в просторі. Кут між прямою і площиною. Точка перетину прямої і площини.

16. Поверхні другого порядку.

Розрахункові завдання

Задача 1. Задані вектори 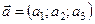, , 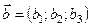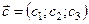і 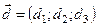в деякому базисі. Переконатись, що вектори 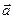, , 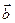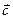утворюють базис і знайти координати вектора в цьому базисі.

1.1. , , , .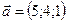

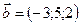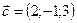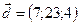1.2. , , , .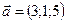

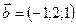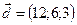1.3. , , , .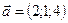

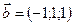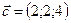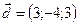1.4. , , , .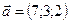

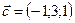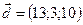1.5. , , , .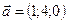

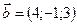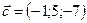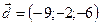1.6. , , , .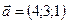

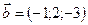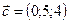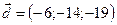1.7. , , , .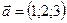

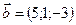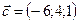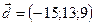1.8. , , , .

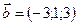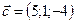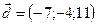1.9. , , , .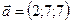

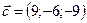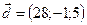1.10. , , , .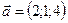

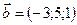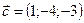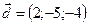1.11. , , , .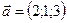

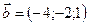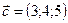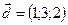1.12. , , , .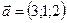

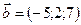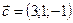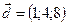1.13. , , , .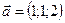

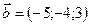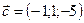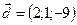1.14. , , , .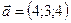

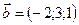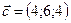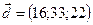1.15. , , , .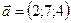

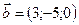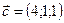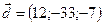1.16. , , , .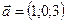

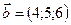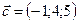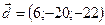1.17. , , , .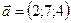

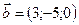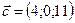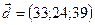1.18. , , , .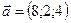

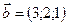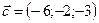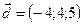1.19. , , , .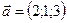

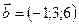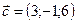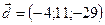1.20. , , , .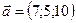

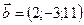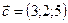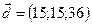1.21. , , , .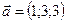

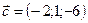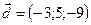1.22. , , , .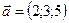

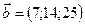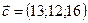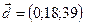1.23. , , , .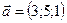

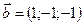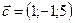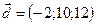1.24. , , , .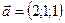

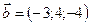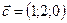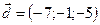1.25. , , , .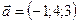

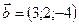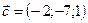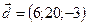1.26. , , , .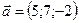

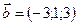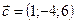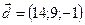1.27. , , , .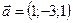

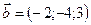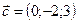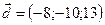1.28. , , , .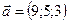

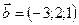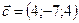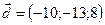1.29. , , , .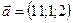

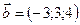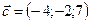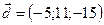1.30. , , , .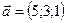

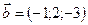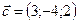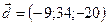Задача 2. Відрізок, обмежений точками 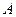та 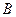, поділили точками 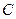і 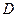у заданому відношенні. Знайти координати цих точок поділу .

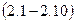2.1. 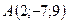, , 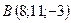1:2:3.

2.2. 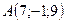, , 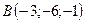2:5:3.

2.3. 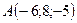, , 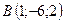4:1:2.

2.4. 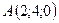, , 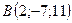2:3:6.

2.5. 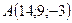, , 3:2:2.

2.6. 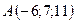, , 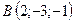2:3:9.

2.7. 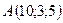, , 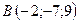3:1:2.

2.8. , , 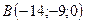3:2:7.

2.9. 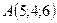, , 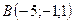2:1:2.

2.10. 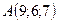, , 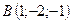3:1:4.

Задано вершини трикутника 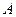, , 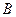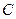. Знайти довжину медіани, проведеної з вершини .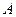

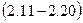2.11. , , .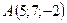

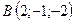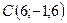2.12. , , .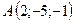

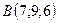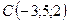2.13. , , .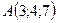

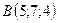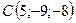2.14. , , .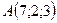

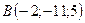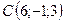2.15. , , .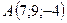

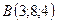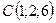2.16. , , .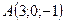

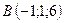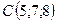2.17. , , .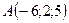

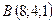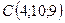2.18. , , .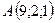

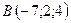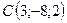2.19. , , .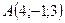

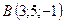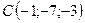2.20. , , .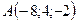

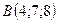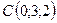В точках 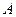і 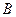прикладені паралельні протилежно напрямлені сили 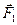і 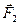. Знайти точку прикладання рівнодійної сили .

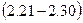2.21. , , , .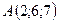

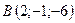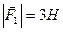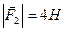2.22. , , , .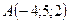

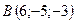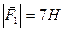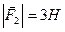2.23. , , , .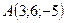

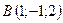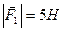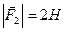2.24. , , , .

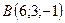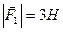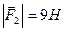2.25. , , , .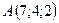

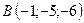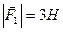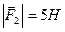2.26. , , , .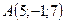

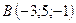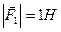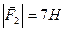2.27. , , , .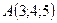

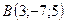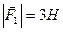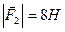2.28. , , , .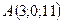

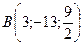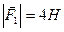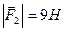2.29. , , , .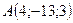

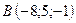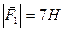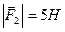2.30. , , , .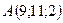

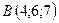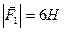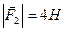Задача 3. Задані точки .Знайти кут між векторами 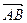та 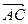і проекцію вектора 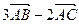на вектор .

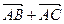3.1. , , .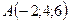

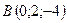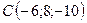3.2. , , .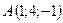

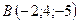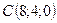3.3. , , .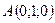

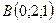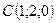3.4. , , .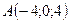

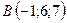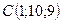3.5. , , .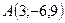

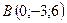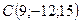3.6. , , .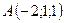

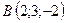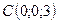3.7. , , .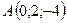

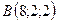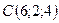3.8. , , .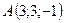

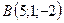3.9. , , .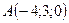

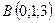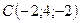3.10. , , .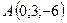

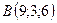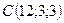3.11. , , .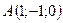

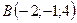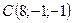3.12. , , .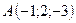

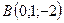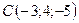3.13. , , .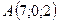

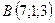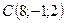3.14. , , .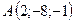

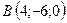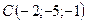3.15. , , .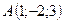

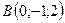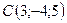3.16. , , .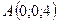

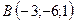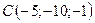3.17. , , .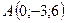

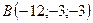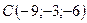3.18. , , .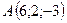

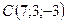3.19. , , .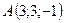

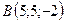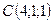3.20. , , .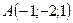

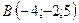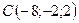3.21. , , .

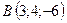3.22. , , .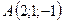

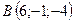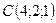3.23. , , .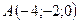

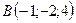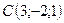3.24. , , .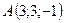

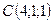3.25. , , .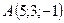

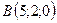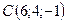3.26. , , .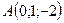

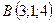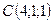3.27. , , .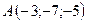

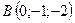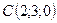3.28. , , .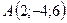

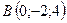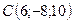3.29. , , .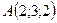

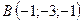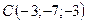3.30. , , .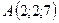

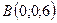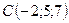Задача 4. Знайти довжину діагоналей і площу паралелограма, побудованого на векторах 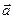та .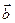

4.1. , .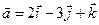

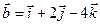4.2. , .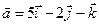

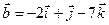4.3. , .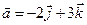

4.4. , .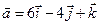

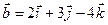4.5. , .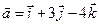

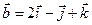4.6. , .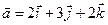

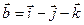4.7. , .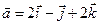

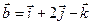4.8. , .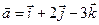

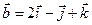4.9. , .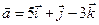

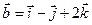4.10. , .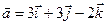

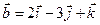4.11. , .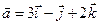

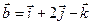4.12. , .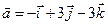

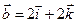4.13. , .

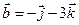4.14. , .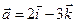

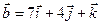4.15. , .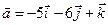

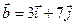4.16. , .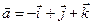

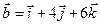4.17. , .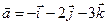

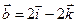4.18. , .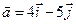

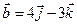4.19. , .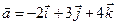

4.20. , .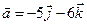

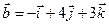4.21. , .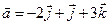

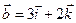4.22. , .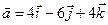

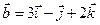4.23. , .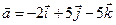

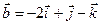4.24. , .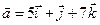

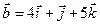4.25. , .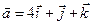

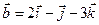4.26. , .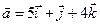

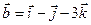4.27. , .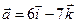

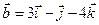4.28. , .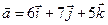

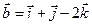4.29. , .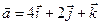

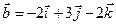4.30. , .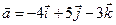

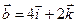Задача 5. Задано вершини трикутника 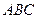. Обчислити довжину висоти, опущеної з вершини 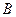на сторону .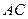

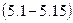5.1. , , .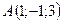

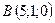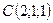5.2. , , .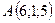

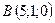5.3. , , .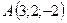

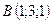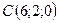5.4. , , .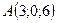

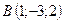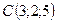5.5. , , .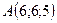

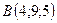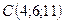5.6. , , .

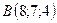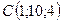5.7. , , .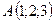

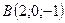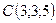5.8. , , .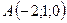

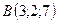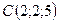5.9. , , .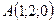

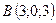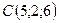5.10. , , .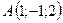

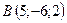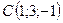5.11. , , .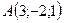

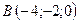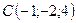5.12. , , .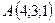

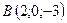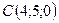5.13. , , .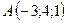

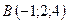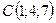5.14. , , .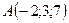

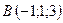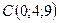5.15. , , .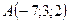

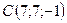Задано сили 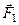, , 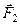, 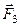прикладені до точки 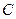. Знайти величину момента рівнодійної цих сил відносно точки .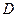

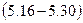5.16. , , ,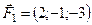

, .

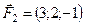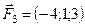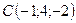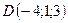5.17. , , ,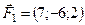

, .

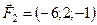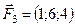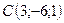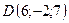5.18. , , ,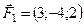

, .

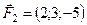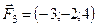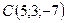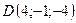5.19. , , ,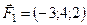

, .

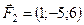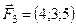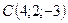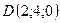5.20. , , ,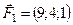

, .

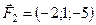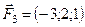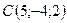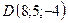5.21. , , ,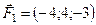

, .

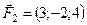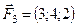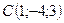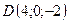5.22. , , ,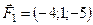

, .

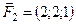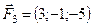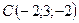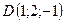5.23. , , ,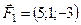

, .

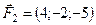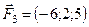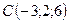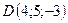5.24. , , ,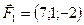

, .

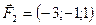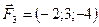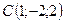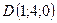5.25. , , ,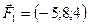

, .

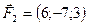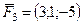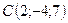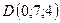5.26. , , ,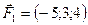

, .

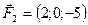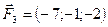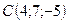5.27. , , ,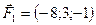

, .

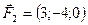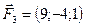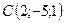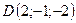5.28. , , ,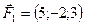

, .

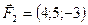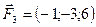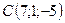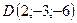5.29. , , ,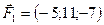

, .

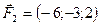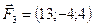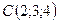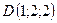5.30. , , ,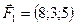

, .

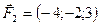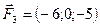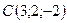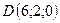Задача 6. Обчислити об’єм тетраедра з вершинами в точках 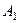, , 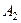, 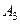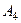і довжину його висоти, опущеної з вершини 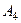на грань .

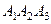6.1. , , , .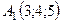

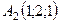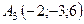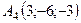6.2. , , , .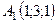

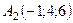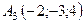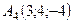6.3. , , , .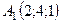

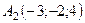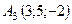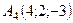6.4. , , , .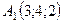

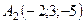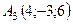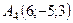6.5. , , , .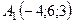

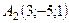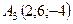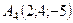6.6. , , , .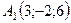

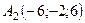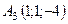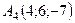6.7. , , , .

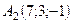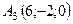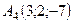6.8. , , , .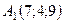

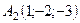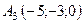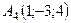6.9. , , , .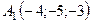

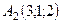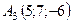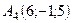6.10. , , , .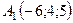

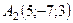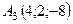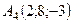6.11. , , , .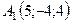

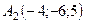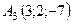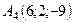6.12. , , , .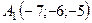

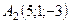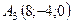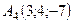6.13. , , , .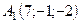

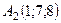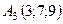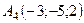6.14. , , , .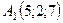

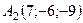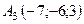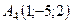6.15. , , , .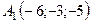

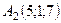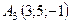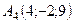6.16. , , , .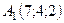

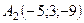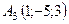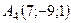6.17. , , , .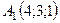

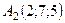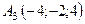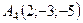6.18. , , , .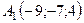

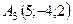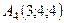6.19. , , , .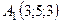

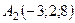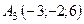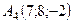6.20. , , , .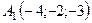

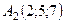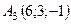6.21. , , , .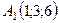

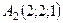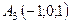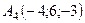6.22. , , , .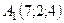

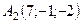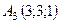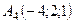6.23. , , , .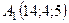

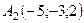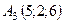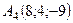6.24. , , , .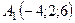

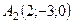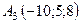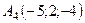6.25. , , , .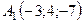

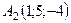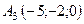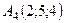6.26. , , , .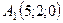

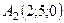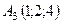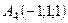6.27. , , , .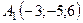

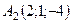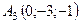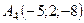6.28. , , , .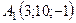

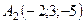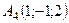6.29. , , , .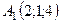

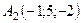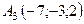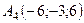6.30. , , , .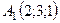

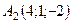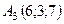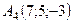Задача 7. Середини сторін трикутника лежать у точках 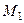, , 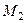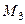. Скласти рівняння сторони трикутника, яка проходить через точку .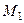

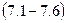7.1. , , .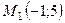

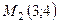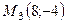7.2. , , .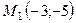

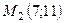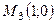7.3. , , .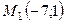

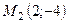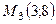7.4. , , .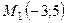

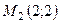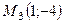7.5. , , .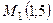

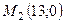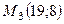7.6. , , .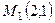

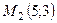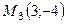Задано вершини трикутника 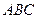. Скласти рівняння висоти трикутника, опущеної з вершини .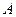

7.7. , , .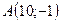

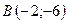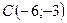7.8. , , .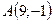

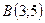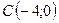7.9. , , .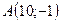

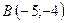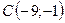7.10. , , .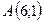

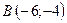7.11. , , .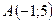

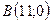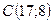7.12. , , .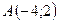

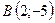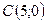Скласти рівняння сторін прямокутника, які проходять через вершину 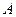, якщо відомі координати сусідньої вершини .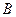

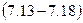7.13. , .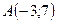

7.14. , .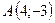

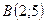7.15. , .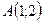

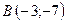7.16. , .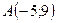

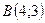7.17. , .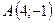

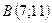7.18. , .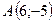

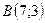Задані координати вершин трикутника 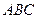. Скласти рівняння прямої, яка проходить через вершину 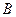паралельно стороні .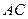

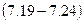7.19. ,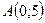

Date: 2015-04-23; view: 504; Нарушение авторских прав